入门平衡树——Treap
前置芝士：
\(\texttt{BST}\)（二叉搜索树）和 \(\texttt{heap}\)（堆）
（其实 \(\texttt{Treap}\) 这个名字就是由 \(\texttt{tree}\) 和 \(\texttt{heap}\) 拼出来的 \(\cdots\)）
\(\texttt{Treap}\)
上回书说道，为了维护 \(\texttt{BST}\) 的平衡，产生了各种平衡树，其中有一种入门级的平衡树—— \(\texttt{Treap}\)。
\(\texttt{Treap}\) 的基本思路
满足 \(\texttt{BST}\) 性质的二叉查找树不是唯一的，他们维护的是一组相同的数值，本质上是等价的。所以我们可以通过在维持 \(\texttt{BST}\) 性质的前提下，通过改变这课二叉搜索树的形态来维持它的左右子树平衡，使树的深度为 \(O(\log n)\) 级别。
而这种既维持了 \(\texttt{BST}\) 性质，又改变了这棵二叉搜索树的形态的方法就是 “旋转”
注意：不是单纯的转，而是可以通过这种方式形象地理解维护平衡的过程。
“单旋转”是最基本的旋转操作，它又分为“左旋”和“右旋”。如下图所示：
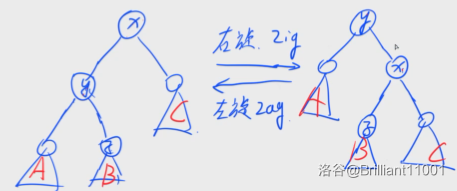
以右旋为例。在初始情况下，\(x\) 是 \(y\) 的左儿子，\(A\) 和 \(B\) 分别是 \(x\) 的左右子树， \(C\) 是 \(y\) 的右子树。
“右旋”操作在维持 \(\texttt{BST}\) 性质的基础上，把 \(x\) 变为 \(y\) 的父节点。因为 \(x\) 的权值小于 \(y\) 的权值，所以 \(y\) 应该做 \(x\) 的右儿子。
当 \(x\) 变成 \(y\) 的父节点后，\(y\) 的左子树就空了出来，于是 \(x\) 原来的右子树 \(B\) 就恰好作为 \(y\) 的左子树。
右旋也叫 \(\operatorname{zig}\)，\(\operatorname{zig(p)}\) 可以理解为把 \(p\) 的左儿子绕着 \(p\) 向右旋转。这里有更形象的解释：
代码：
void zig(int &p) {
int q = tr[p].ls;
tr[p].ls = tr[q].rs, tr[q].rs = p, p = q;
}
左旋也叫 \(\operatorname{zag}\)，\(\operatorname{zag(p)}\) 可以理解为把 \(p\) 的右儿子绕着 \(p\) 向左旋转。 由于原理和右旋一样，就只放代码了：
void zag(int &p) {
int q = tr[p].rs;
tr[p].rs = tr[q].ls, tr[q].ls = p, p = q;
}
经过一系列合理的旋转，就可以使 \(\texttt{BST}\) 变得平衡了。比如：
那么，什么才是“合理”的旋转操作呢？上篇文章提到了：在随机数据下，普通的 \(\texttt{BST}\) 是趋于平衡的。\(\texttt{Treap}\) 的思想就是利用“随机”来创造平衡条件。因为在旋转过程中必须维持 \(\texttt{BST}\) 性质，所以 \(\texttt{Treap}\) 就把“作用在堆性质上。
\(\texttt{Treap}\) 在插入每个新节点时，给该节点随机生成一个额外的权值。然后像堆的插入操作一样，从下往上一次检查，若有节点不满足大根堆的性质，就执行单旋转，使该节点与其父节点的位置对换。具体的，由于单旋转操作会使当前节点的位置下降 \(1\) 而使其儿子位置上升 \(1\)，所以若左边不满足就右旋，右边不满足就左旋。
顺便贴上大佬总结的绕口令口诀：
左旋拎右左挂右，右旋拎左右挂左——AgOH
插入
基本思路和朴素的 \(\texttt{BST}\) 相同，唯一增加的操作就是维护堆性质，即在每次插入时判断插入的节点是否满足堆性质，然后相应地进行旋转操作。
void insert(int &p, int key) {
if(p == 0) p = New(key);
else if(tr[p].key == key) tr[p].cnt++;
else if(key < tr[p].key) {
insert(tr[p].ls, key);
if(tr[tr[p].ls].val > tr[p].val) zig(p); //左大右旋
}
else {
insert(tr[p].rs, key);
if(tr[tr[p].rs].val > tr[p].val) zag(p); //右大左旋
}
}
删除
删除其实是一个删繁就简的过程：先检索到需要删除的节点，然后不断把它旋转成为叶结点，然后直接删掉就行了。这样就可以避免朴素 \(\texttt{BST}\) 的删除方法导致的节点更新、堆性质维护等复杂问题。
代码：
void remove(int &p, int key) {
if(!p) return ;
if(key == tr[p].key) {
if(tr[p].cnt > 1) tr[p].cnt--;
else if(tr[p].ls || tr[p].rs) {
if(tr[tr[p].ls].val > tr[tr[p].rs].val && !tr[p].rs) {
zig(p); //左大右旋
remove(tr[p].rs, key);
}
else {
zag(p); //右大左旋
remove(tr[p].ls, key);
}
}
else p = 0;
}
else if(key < tr[p].key) remove(tr[p].ls, key);
else remove(tr[p].rs, key);
}
求前驱/后继
和朴素的 \(\texttt{BST}\) 完全相同，略过。
例题 P3369 【模板】普通平衡树
在这道例题中由于有根据权值求排名和根据排名求权值两个操作，所以多维护几个值：\(cnt\)（该权值出现次数）、\(siz\)（以该节点为根的子树大小）。
同时还要新加入一个 \(\operatorname{pushup}\) 操作，来通过子节点的信息更新父节点的信息，从而维护上述两个值。
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
struct Treap {
int ls, rs; //左右儿子的下标
int key, val; //key 代表权值，val 是随机赋的值
int cnt, siz;
}tr[N];
int n, root, idx, inf = 0x7ffffff;
int New(int key) {
tr[++idx].key = key;
tr[idx].val = rand();
tr[idx].cnt = tr[idx].siz = 1;
return idx;
}
inline void pushup(int p) {tr[p].siz = tr[tr[p].ls].siz + tr[tr[p].rs].siz + tr[p].cnt;}
void zig(int &p) {
int q = tr[p].ls;
tr[p].ls = tr[q].rs, tr[q].rs = p, p = q;
pushup(tr[p].rs), pushup(p); //从下往上更新
}
void zag(int &p) {
int q = tr[p].rs;
tr[p].rs = tr[q].ls, tr[q].ls = p, p = q;
pushup(tr[p].ls), pushup(p); //从下往上更新
}
void build() {
New(-inf);
New(inf);
root = 1;
tr[1].rs = 2;
pushup(root);
if(tr[1].val < tr[2].val) zag(root); //由于初始节点赋的 val 可能不满足堆性质，所以也要旋一下
}
void insert(int &p, int key) {
if(p == 0) p = New(key);
else if(tr[p].key == key) tr[p].cnt++;
else if(key < tr[p].key) {
insert(tr[p].ls, key);
if(tr[tr[p].ls].val > tr[p].val) zig(p);
}
else {
insert(tr[p].rs, key);
if(tr[tr[p].rs].val > tr[p].val) zag(p);
}
pushup(p); //每次操作完都要进行更新
}
void remove(int &p, int key) {
if(!p) return ;
if(key == tr[p].key) {
if(tr[p].cnt > 1) tr[p].cnt--;
else if(tr[p].ls || tr[p].rs) {
if(tr[tr[p].ls].val > tr[tr[p].rs].val && !tr[p].rs) {
zig(p);
remove(tr[p].rs, key);
}
else {
zag(p);
remove(tr[p].ls, key);
}
}
else p = 0;
}
else if(key < tr[p].key) remove(tr[p].ls, key);
else remove(tr[p].rs, key);
pushup(p); //每次操作完都要进行更新
}
int get_rank(int p, int key) {
if(!p) return 0;
if(key == tr[p].key) return tr[tr[p].ls].siz;
if(key < tr[p].key) return get_rank(tr[p].ls, key);
else return tr[tr[p].ls].siz + tr[p].cnt + get_rank(tr[p].rs, key);
}
int get_num(int p, int pos) {
if(!p) return inf;
if(tr[tr[p].ls].siz >= pos) return get_num(tr[p].ls, pos);
if(tr[tr[p].ls].siz + tr[p].cnt >= pos) return tr[p].key;
return get_num(tr[p].rs, pos - tr[tr[p].ls].siz - tr[p].cnt);
}
int get_pre(int p, int key) {
if(!p) return -inf;
if(key <= tr[p].key) return get_pre(tr[p].ls, key);
return max(tr[p].key, get_pre(tr[p].rs, key));
}
int get_next(int p, int key) {
if(!p) return inf;
if(key >= tr[p].key) return get_next(tr[p].rs, key);
return min(tr[p].key, get_next(tr[p].ls, key));
}
int main() {
build();
scanf("%d", &n);
int op, x;
while(n--) {
scanf("%d%d", &op, &x);
if(op == 1) insert(root, x);
else if(op == 2) remove(root, x);
else if(op == 3) printf("%d\n", get_rank(root, x));
else if(op == 4) printf("%d\n", get_num(root, x + 1)); //由于有负无穷的哨兵，所以要 +1 才是真正排名
else if(op == 5) printf("%d\n", get_pre(root, x));
else printf("%d\n", get_next(root, x));
}
return 0;
}
