暴力数据结构——ODT 珂朵莉树

\(\texttt{Origin}\)

\(\texttt{ODT (Old Driver Tree)}\)，中文名珂朵莉树。

有人为了 CF896C 发明了这个算法，这道题又和珂朵莉有关，所以这个算法叫做珂朵莉树。

另外，由于发明者 \(\texttt{lxl}\) 的原因，也珂叫 \(\texttt{ODT (Old Driver Tree)}\)。

也有个正统名字叫颜色段均摊，但是还是叫珂朵莉树好听。

\(\texttt{0x00}\) 前言

之所以突然想学这个数据结构是因为之前做了一道题 SP13015，看到的第一眼就是线段树，等到把这道题 A 了之后打开标签才发现是珂朵莉树，出于好奇心的驱使，才有了这篇博客。

珂朵莉可爱捏！

前置芝士：\(\texttt{set}\)（现在知道为什么上一篇博客是 \(\texttt{set}\) 的学习笔记了吧）

Warning！

\(\texttt{ODT}\) 可以 可以解决一些线段树不能解决的问题，如区间次幂求和。

但要求数据随机，随机下跑得很快，开了 \(O2\) 更快。

数据不随机时间复杂度就是 \(O(nm)\)，开了 \(O2\) 也没用。

\(\texttt{0x01}\) 珂朵莉树珂以解决什么问题

对一个序列，进行一个区间推平操作。就是把一个范围内，比如 \([l,r]\) 范围内的数字变成同一个。可能除了推平以外，还夹杂其他操作。如果数据是随机的，就可以用珂朵莉树啦。

\(\texttt{0x02}\) 基本结构

由于区间推平操作，所以序列中的数是一段一段的，而且每一段是同一个数。

所以我们将每个这样的区间打包成一个三元组 \([l,r,val]\)，分别代表：左端点、右端点和值。然后将所有这样整合后的三元组插到一个 \(\texttt{set}\) 里去维护。

这样的话，只需要一个结构体就行了。

struct node{
	int l, r;
	mutable ll val; //mutable 方便以后修改
	node(int l_ = 0, int r_ = -1, ll val_ = 0) :l(l_), r(r_), val(val_) {}
	bool operator <(const node &other) const{ //重载成小于
		return l < other.l;
	}
};
typedef set<node>::iterator IT;
set <node> s;

借大佬的图一用 \(\sim\)

\(\texttt{0x03}\) 基本操作

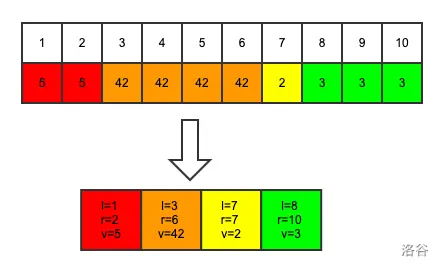
核心操作： \(\texttt{split}\)

在推平操作的进行中，一些区间可能要被合并成一个区间，也可能被分成几个新区间。

这时候就需要用到 \(\operatorname{split}\) 函数，它的作用是给定一个位置 \(pos\)，然后找到包含 \(pos\) 的区间，将其分成 \([l,pos - 1]\) 和 \([pos,r]\) 两个区间，最后返回指向 \([pos,r]\) 的迭代器。当然，如果 \(pos\) 本身就是一个区间的开头，就不用切割了，直接返回这个区间的迭代器。

IT split(int pos) {
	IT it = s.lower_bound(node(pos)); //按 l 找包含 pos 的 node
	if(it != s.end() && it -> l == pos) return it; //若 pos 是一个区间的开头，就直接返回该区间迭代器
   --it; //由于找到的是 pos 后面的区间，所以要先--才是包含它的区间
	int l = it -> l, r = it -> r;
	ll val = it -> val;
	s.erase(it); //先把此区间删除
	s.insert(node(l, pos - 1, val)); //插入切割后的第一个区间
	return s.insert(node(pos, r, val)).first; //插入切割后的第二个区间并返回值
	//insert函数返回pair，其中的first是新插入结点的迭代器
}

那么我们按照 \(pos\) 创建一个 \(node\) ，然后去查询，就找到了 \(it\) 这个位置。这个时候有三种情况，一种是我们正好找到了一个区间，它是以 \(pos\) 开头的，所以就对应了代码中的第一个 \(\operatorname{if}\) 判断，这时候直接返回这个区间的迭代器 \(it\)。

还有两种情况是，我们找到的这个区间是正好比包含 \(pos\) 的区间大一点点的，或者 \(pos\) 太大了，超过了最后一个区间的右端点。不管怎样先把 \(it\) 往前挪一个格，然后这时候看看 \(it\) 的右端点，如果比 \(pos\) 小，说明是 \(pos\) 太大了，就直接返回 \(\operatorname{s.end()}\)。否则的话，现在 \(it\) 就是应该包含了 \(pos\) 的那个区间。这时候，我们要把它一分为二，把原来的那个区间删掉，然后插入两个新区间，分别是 \([l,pos-1]\) 和 \([pos,r]\)。

\(\texttt{assign}\)

对应区间推平操作。因为区间 \([l,r]\) 可能与其他节点代表的区间有交集，所以我们要先把 \(l\) 和 \(r\) \(\operatorname{split}\) 出来，将其中的节点全删掉，最后再插入\(\{l,r,val\}\)。

void assign(int l, int r, ll val) {
	IT itr = split(r + 1), itl = split(l);
	s.erase(itl, itr);
	s.insert(node(l, r, val));
}

注意： 必须要先 \(\operatorname {split(r+1)}\)，再 \(\operatorname {split(l)}\)。

比如现在要从 \([3,5]\) 中分离出 \([3,4]\)，则要执行 \(\operatorname {split(3)}\) 和 \(\operatorname {split(5)}\)。若先执行后者，再执行前者，则 \(itl\) 指向代表 \([3,5]\) 的 \(node\)，\(itr\) 指向代表 \([5,5]\) 的 \(node\)，但是这时代表 \([3,5]\) 的 \(node\) 已经被删除了，调用 \(\operatorname {erase}\) 时就会出问题，导致 RE。

其他操作

void change(int l, int r, ll val) { //暴力套就完事了
	IT itr = split(r + 1), itl = split(l);
	for(IT it = itl; it != itr; it++) {
		//to do
	}
}

\(\texttt{0x04}\) 时间复杂度

珂朵莉树只有当数据随机时才有比较好的表现，这是因为她的时间复杂度是期望复杂度。比如一共有 \(4\) 种操作，在随机数据下，进行区间推平的概率为 \(\frac{1}{4}\)，对于每次区间推平操作，都相当在一整条线段上选取一段，期望长度为整个线段长度的 \(\frac{1}{3}\)，而每次平推操作都会删除掉此区间内的其他区间节点，所以每次操作后 set 的长度都会变成原来的 \(\frac{2}{3}\)。所以一波操作下来，\(\texttt{set}\) 的长度就变为了 \(O(\log n)\)，所以时间复杂度约为 \(O(q\log n)\)。

以上只是我方便自己理解的粗略证明，严谨、正确性方面不保证。

好好好，正确又严谨的证明如下：（再次借大佬的图）