高级数据结构(一)树状数组
引入
根据任意正整数关于
其中,
不妨设
- 长度为
- 长度为
- 长度为
m. 长度为
这些小区间的共同特点是:若区间结尾为
给定一个整数
while(x > 0) {
printf("[%d, %d]\n", x - (x & -x) + 1, x);
x -= x & -x;
}
1.树状数组简介
树状数组(
树状数组支持的操作:
1. 区间和、区间异或和、区间乘积和 RMQ(显然,支持的操作都具有交换律,这也算是树状数组的一大特性吧)
2. 单点修改(朴素的树状数组结构不支持区间修改,当然也可以普及成区间修改结构)
功能听起来和前缀和数组有点像,但它的优势在哪呢?
以求区间和为例,我们知道,前缀和数组求区间和的时间复杂度为
树状数组平均了一下,两种操作的时间复杂度都是
2.树状数组的存储特点:
对于给定的序列
为什么它叫做树状数组呢?事实上,数组
- 每个内部节点
- 每个内部节点
- 除树根外,每个内部节点
- 树的深度为
如果
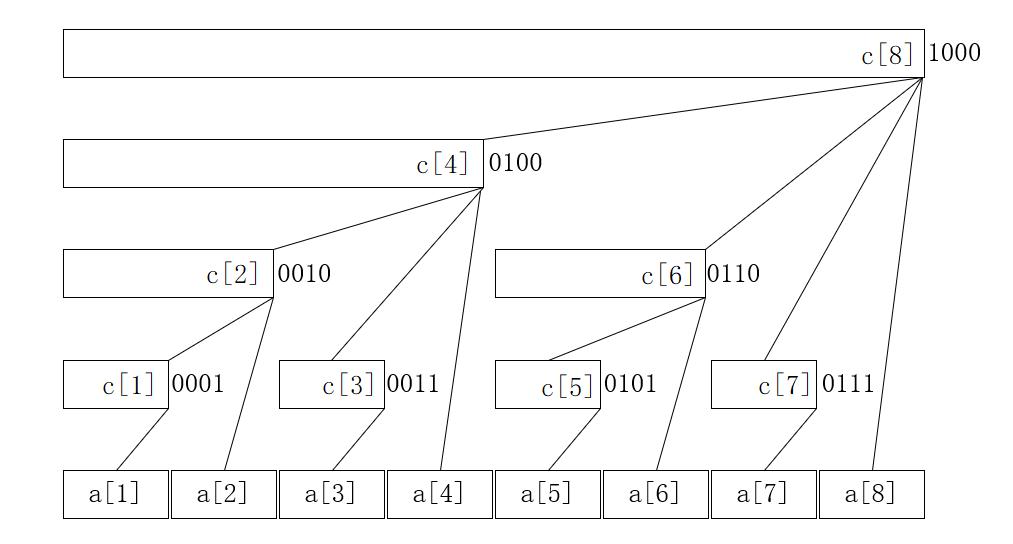
由图可知:
3.树状数组的实现
在执行所有操作之前,我们需要对树状数组进行初始化——针对原始序列
为了简便起见,比较一般的初始化方法是:直接建立一个全为
更高效的初始化方法是:从小到大依次考虑每个节点
快速初始化:
void init() {
for (int i = 1; i <= n; i++) {
pre[i] = pre[i - 1] + a[i];
c[i] = pre[i] - pre[i - lowbit(i)];
}
}
查询前缀和:
int ask(int x) {
int res = 0;
for(; x; x -= lowbit(x)) res += c[x];
return res;
}
单点修改:
void add(int x, int y) {
for(; x <= n; x += lowbit(x)) c[x] += y;
}
P3374 【模板】树状数组 1
单点询问 + 区间修改:
利用了差分的思想,维护一个差分数组
P3368 【模板】树状数组 2
区间询问 + 区间修改:
(话说这不就是线段树吗)
说实话,树状数组不仅跑得比线段树快,码量要比线段树小得多,就是比较难想。
P3372 【模板】线段树 1
P2357 守墓人
#include <iostream>
using namespace std;
const int N = 5000010;
typedef long long ll;
int n, m;
ll c[2][N];
int lowbit(int x) {
return x & -x;
}
ll ask(int id, int x) {
ll res = 0;
for(; x; x -= lowbit(x)) res += c[id][x];
return res;
}
void add(int id, int x, ll y) {
for(; x <= n; x += lowbit(x)) c[id][x] += y;
}
int main() {
scanf("%d%d", &n, &m);
ll a, las = 0;
for(int i = 1; i <= n; i++) {
scanf("%lld", &a);
add(0, i, a - las);
add(1, i, (i - 1) * (a - las));
las = a;
}
int op, x, y;
ll k;
while(m--) {
scanf("%d%d%d", &op, &x, &y);
if(op == 1) {
scanf("%lld", &k);
add(0, x, k);
add(0, y + 1, -k);
add(1, x, (x - 1) * k);
add(1, y + 1, -y * k);
}
else {
printf("%lld\n", y * ask(0, y) - ask(1, y) - (x - 1) * ask(0, x - 1) + ask(1, x - 1));
}
}
return 0;
}



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】