动态规划(二)(线性DP、区间DP)
一.线性DP
所谓线性DP,就是说它的动态转移方程是线性的。
线性DP有三个经典的例题,如下:
1. LIS (Longest Increasing Subsequence,最长上升子序列)问题
问题描述:给定一个长度为
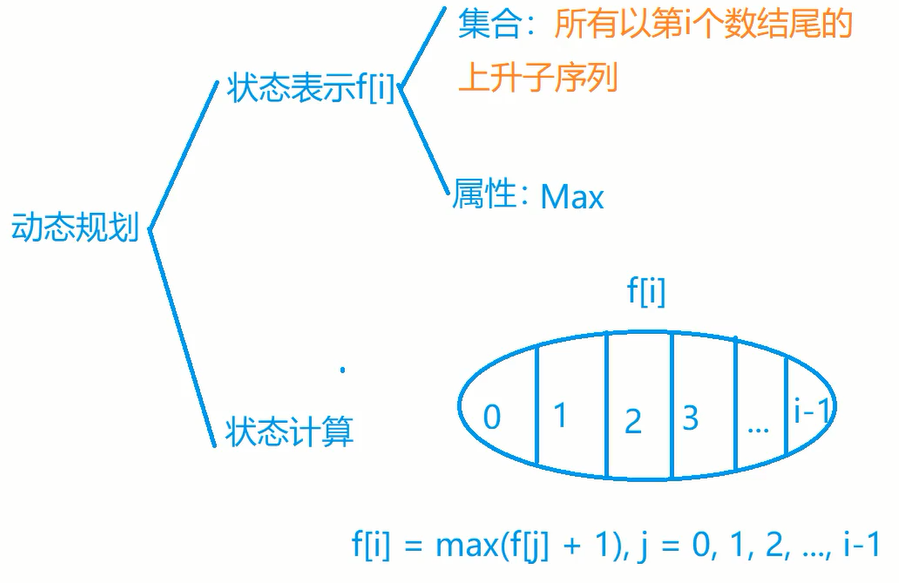
朴素做法:
状态表示:
状态计算(集合划分):
有一个边界,若前面没有比i小的,
最后再找
时间复杂度
代码如下:
#include <iostream>
using namespace std;
const int N = 1010;
int n;
int a[N], dp[N];
int main() {
scanf("%d", &n);
for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
for(int i = 1; i <= n; i++) {
dp[i] = 1;
for(int j = 1; j < i; j++) {
if(a[i] > a[j]) dp[i] = max(dp[i], dp[j] + 1);
}
}
int ans = 0;
for(int i = 1; i <= n; i++) {
ans = max(ans, dp[i]);
}
printf("%d\n", ans);
return 0;
}
优化版:
我们其实不难看出,对于
将原来的dp数组的存储由数值换成该序列中,上升子序列长度为i的上升子序列,的最小末尾数值。
这其实就是一种几近贪心的思想:我们当前的上升子序列长度如果已经确定,那么如果这种长度的子序列的结尾元素越小,后面的元素就可以更方便地加入到这条我们臆测的、可作为结果、的上升子序列中。
代码如下:
#include <iostream>
using namespace std;
const int N = 100010;
int n;
int a[N];
int dp[N]; //dp[i]表示长度为i的子序列的结尾的最小值为多少
int main() {
scanf("%d", &n);
for(int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
dp[i] = 0x3f3f3f3f;
}
dp[1] = a[1];
int len = 1;
for(int i = 2; i <= n; i++) {
int l = 1, r = len;
if(a[i] > dp[len]) dp[++len] = a[i]; //若当前处理的这一项大于末尾,则向后填充
else { //否则就向前寻找第一个比它小的数(因为dp数组必然单调,所以可以二分)
while(l < r) { //其实就是lower_bound(),手写要快一些
int mid = l + r >> 1;
if(dp[mid] >= a[i]) r = mid;
else l = mid + 1;
}
dp[l] = a[i];
}
}
printf("%d\n", len);
return 0;
}
B3637
2. LCS (Longest Common Subsequence,最长公共子序列)问题
问题描述:给定两个长度分别为
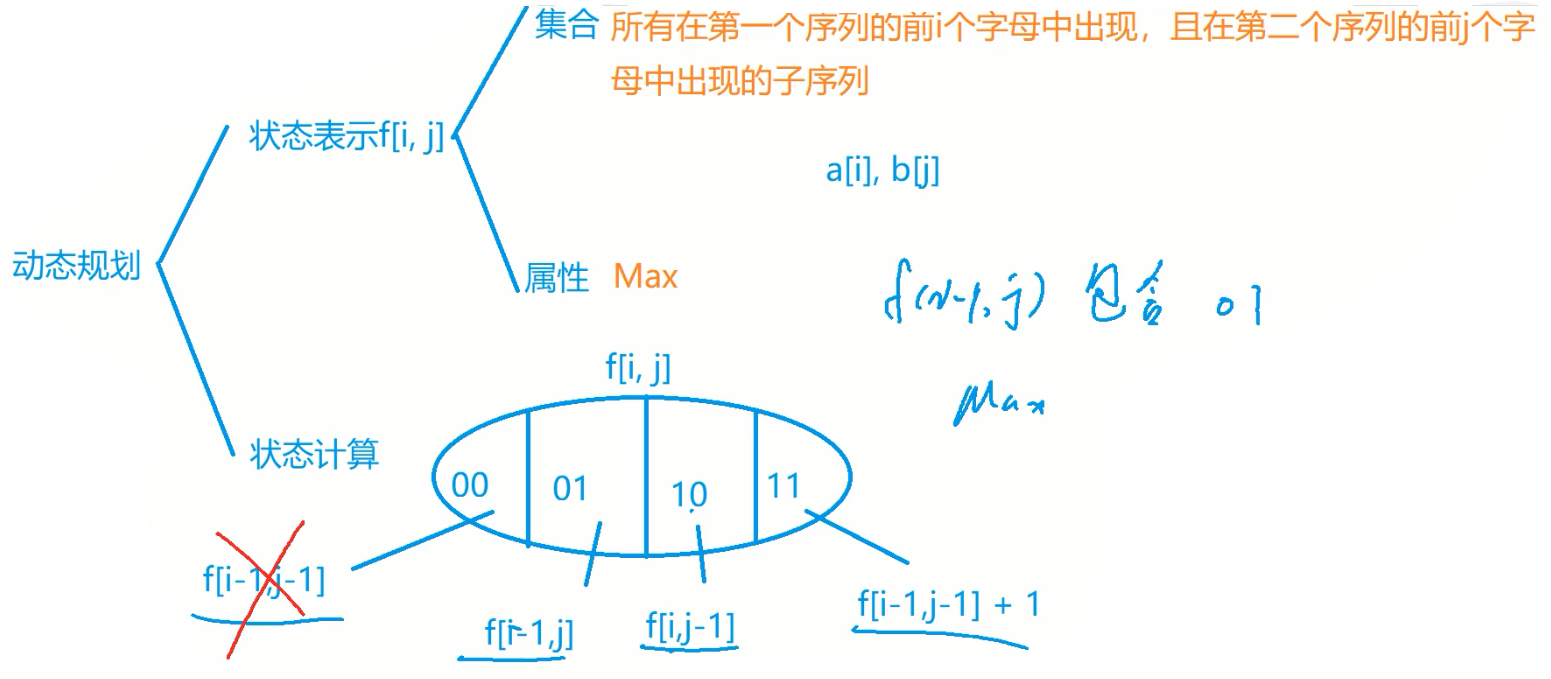
集合表示:
集合划分:以
①
②
看似是
例如:要求
③
④
实际上,在计算时,①包含在②和③的情况中,所以①不用考虑
代码如下:
#include <iostream>
using namespace std;
const int N = 1010;
int n, m, f[N][N];
char a[N], b[N];
int main() {
cin >> n >> m >> a + 1 >> b + 1;
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= m; j++) {
f[i][j] = max(f[i - 1][j], f[i][j - 1]);
if(a[i] == b[j]) f[i][j] = max(f[i][j], f[i - 1][j - 1] + 1);
}
}
printf("%d", f[n][m]);
return 0;
}
二.区间DP
它以“区间长度”作为DP的“阶段”,使用两个坐标(区间的左右端点)描述每个维度,本质上它也属于线性DP的一种。
P1775 石子合并(弱化版)
思维导图:
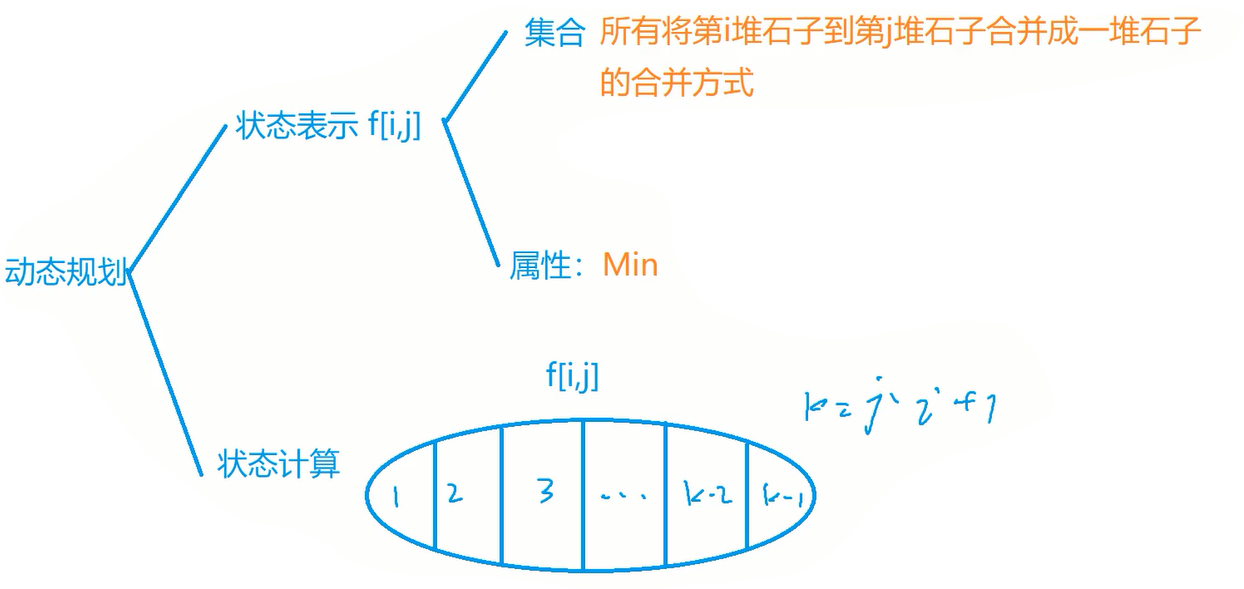
由于只能合并相邻的两堆石子,所以最后一次合并时一定是左边连续的一部分和右边连续的一部分合并。
集合划分: 以最后一次合并时的分界限进行分类。
状态表示:
状态计算:
(1)
(2)
问题答案:
所有的区间
区间
for (int len = 1; len <= n; len++) { // 区间长度
for (int i = 1; i + len - 1 <= n; i++) { // 枚举起点
int j = i + len - 1; // 区间终点
if (len == 1) {
dp[i][j] = 初始值
continue;
}
for (int k = i; k < j; k++) { // 枚举分割点,构造状态转移方程
dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j] + w[i][j]);
}
}
}
本题代码如下:
#include <iostream>
using namespace std;
const int N = 310;
int n;
int s[N];
int dp[N][N];
int main() {
scanf("%d", &n);
for(int i = 1; i <= n; i++) scanf("%d", &s[i]);
for(int i = 2; i <= n; i++) s[i] += s[i - 1];
for(int len = 2; len <= n; len++) {
for(int i = 1; i + len - 1 <= n; i++) {
int l = i, r = i + len - 1;
dp[l][r] = 0x3f3f3f3f;
for(int k = l; k < r; k++) {
dp[l][r] = min(dp[l][r], dp[l][k] + dp[k + 1][r] + s[r] - s[l - 1]);
}
}
}
printf("%d\n", dp[1][n]);
return 0;
}



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· 单线程的Redis速度为什么快?
· SQL Server 2025 AI相关能力初探
· AI编程工具终极对决:字节Trae VS Cursor,谁才是开发者新宠?
· 展开说说关于C#中ORM框架的用法!