洛谷P9573 「TAOI-2」核心共振题解

题目传送门

题意：

构造一个 \(1\sim n\) 的排列，使得其中两个相邻的数之和为 \(p\) 的倍数，且这种情况在序列中尽量多的存在。

分析：

我采用了由特殊到一般的方法。以 \(p = 2\) 为例，要想使两个数之和为 \(2\) 的倍数，那么肯定是两个偶数或两个奇数进行两两组合。

想到这里不妨放开思路：奇数和偶数在这里究竟是什么样的存在呢？很容易发现，奇数除以 \(2\) 余数是 \(1\) ，偶数则为 \(0\) ，所以我们完全可以把 \(1\sim n\) 中的所有数分成两类：除以 \(2\) 余数为 \(0\) 的和除以 \(2\) 余数为 \(1\) 的。

这很像 hash 的处理思路，将 \(1\sim n\) 中的所有数都对 \(p\) 取模后得到在 \(0\sim p - 1\) 之间的数。也就是说：\(1\sim n\) 上的所有数都可以映射到 \(0\sim p - 1\) 上！

那么接下来就好办了。首先考虑特殊情况，所有的数都是 \(1\) 的倍数，所以当 \(p = 1\) 时，直接按 \(1\sim n\) 输出即可。同时如果 \(p\) 太大了，连最大的两个数 \(n - 1\) 和 \(n\) 相加都没它大，那此时不可能产生共振，也是直接按 \(1\sim n\) 输出即可。

一般情况下，将模为 \(0\) 的数先输出出来，因为它们本就是 \(p\) 的倍数了，相加后还是 \(p\) 的倍数。然后设这两个数分别为 \(a\) , \(b\) ，要使 \(a + b\) 为 \(p\) 的倍数，则需要满足 \(a \bmod p + b \bmod p = p\) ，即将余数为 \(i\) 和余数为 \(p - i\) 的两组数交替输出即可。

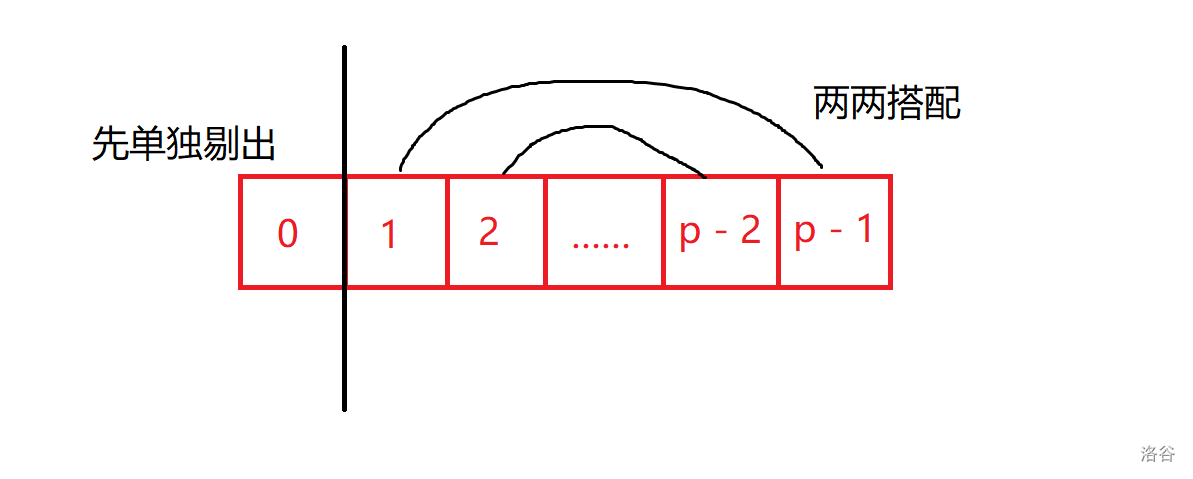
若 \(p\) 是奇数，那在除去 \(0\) 这一组后刚好形成两两搭配；若 \(p\) 是偶数，那还有一组是落单的，发现其实落单的那组中的成员数两两相加也是 \(p\) 的倍数，所以直接输出这一组就行了。

代码：

#include <iostream>
#include <cstring>

using namespace std;
const int N = 200010; 
int t, n, p;

inline int read() {	
    char ch = getchar();
	int x = 0, f = 1;
    while(ch < '0' || ch > '9') {
        if(ch == '-') f = -1;
        ch = getchar();
    } 
	while(ch >= '0' && ch <= '9'){
        x = x * 10 + ch - '0';
        ch = getchar();
    } 
    return x * f;
}

int main() {
	t = read();
	while(t--) {
		n = read();
		p = read();
		if(p == 1 || p > 2 * n - 1) { //特判 
			for(int i = 1; i <= n; i++) printf("%d ", i);
			continue;
		}
		for(int i = p; i <= n; i += p) { //0
			printf("%d ", i);
		}
		for(int i = 1; i < p; i++) { //1 ~ p - 1
			if(i >= p - i) break; //若前面的组比后面的组编号还大说明输出完了 
			for(int j = 0; j <= n; j += p) {
				if(i + j <= n) printf("%d ", i + j); 
				if(p - i + j <= n) printf("%d ", p - i + j); //在n的范围内才输出 
			}
		}
		if(p % 2 == 0) { //p为偶数则输出中间那组 
			for(int i = p / 2; i <= n; i += p) {
				printf("%d ", i);
			}
		}
	}
	return 0; //完结撒花！ 
}