数据结构复习2

合集 - 数据结构(19)

1.树状数组套权值线段树（带修主席树）2024-07-23 2.可持久化数据结构2024-07-23 3.高贵的伸展树——Splay2024-07-23 4.入门平衡树——Treap2024-02-01 5.二叉搜索树（BST）2024-02-01 6.暴力数据结构——ODT 珂朵莉树2024-02-01 7.STL之——set2024-02-01 8.最实用之数据结构思想——分块2024-01-23 9.高级数据结构（一）树状数组2024-01-23 10.从零开始掌握线段树大法2024-01-23

11.数据结构复习22023-09-26

12.离线分治算法：cdq 分治2024-07-23 13.笛卡尔树2024-07-23 14.【进阶】树状数组的高阶应用2024-08-04 15.SP30906 解题报告2024-09-04 16.SP17123 解题报告2024-09-15 17.P11208 解题报告2024-10-22 18.NOIP 冲刺之——数据结构01-19 19.浅谈扫描线2024-02-01

5.并查集

它有两个功能：将两个集合合并和询问两个元素是否在同一个集合内。

不妨设想一下，假如不使用并查集，用暴力的做法，那么第一个操作的时间复杂度约为 $O (n)$ ，第二个操作的时间复杂度为 $O (1)$ ，第一个操作的时间复杂度较高。

但如果使用了并查集，则可以将近 $O (1)$ 的时间来完成这两个操作。

基本原理：用树的形式来维护每个集合，集合的编号就是根节点的编号。对于树的每一个节点都记录它的父节点， $p [x]$ 表示 $x$ 的父节点。

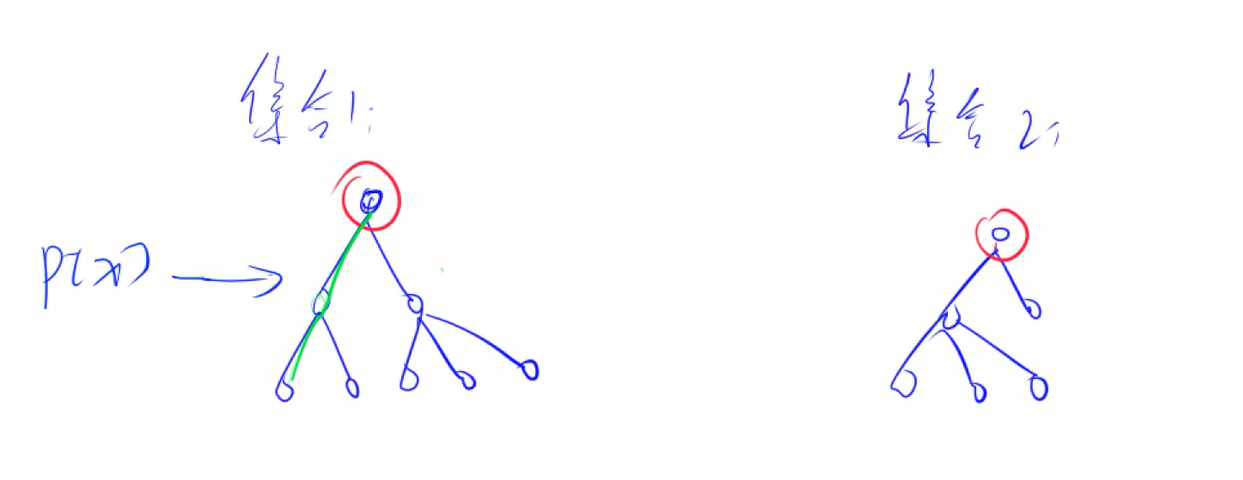
Q1：如何判断树根？

A1：对于每个非树根点，它的父节点都不是它本身，树根的父节点是它本身。

if(p[x] == x)

Q2：如何求x的集合编号？

A2：

while(p[x] != x) x = p[x];

Q3：如何合并两个集合？

A3：假设 $x$ 是 $A$ 的集合编号， $y$ 是 $B$ 的集合编号。则令 $p [x] = y$ 即可。

但是求集合编号的时间复杂度还是挺高的，优化：路径压缩。就是说当搜到根节点后，将搜索时经过的点的父节点直接指向根节点。

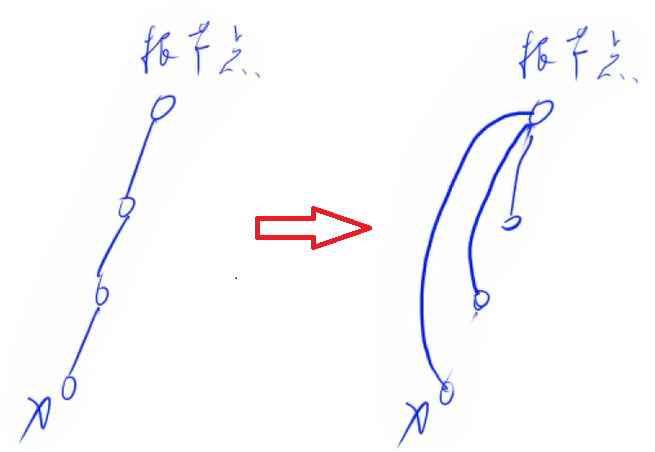
上模板题！

6.堆

堆是一棵完全二叉树，同时它的每棵子树也是堆。

总结得太全面啦！

（这里复习手写堆）

手写堆支持 $5$ 种操作：

1.插入一个数
2.求集合当中的的最小值
3.删除最小值
4.删除任意一个元素
5.修改任意一个元素

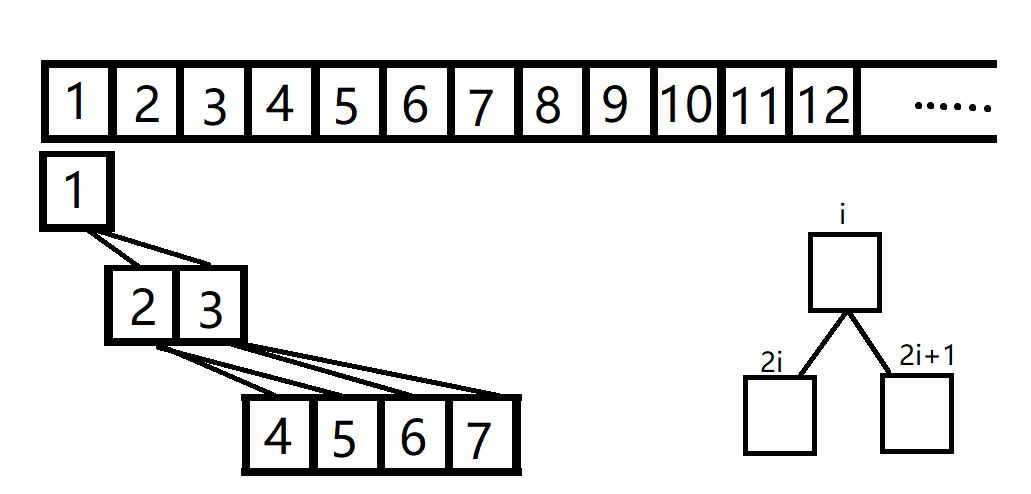
堆的储存：用一维数组来储存堆，其中,根节点储存在下标 $1$ 的位置中，对于任意下标为 $i$ 的节点，其左节点下标为 $2 i$ ，其右节点下标为 $2 i + 1$ 。

如图所示：

基本操作：(以小根堆为例）

$up(x)$ ：假如堆中有个元素变小了，那么我们需要将它向上移，使所有的子节点比父节点大。
$down(x)$ ：假如堆中有个元素变大了，那么我们需要将它向下移，使所有的父节点比子节点小。

比如：

//插入一个数
heap[++size] = x, up(size);
//求集合当中的的最小值
cout << heap[1] << endl;
//删除最小值
heap[1] = heap[size], size--, down(1);
//删除任意一个元素
heap[x] = heap[size], size--, down(x), up(x);
//修改任意一个元素
heap[x] = k, down(x), up(x);

//上移
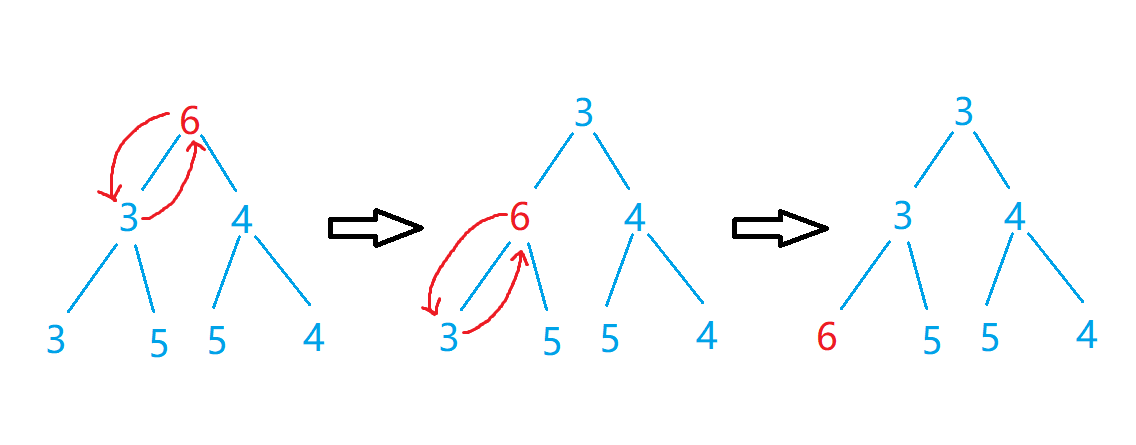
void up(int x) { //O(log n) （大根堆反过来）
	while(x / 2 && heap[x] < heap[x / 2]) { //若父节点大于子节点
		swap(heap[x], heap[x / 2]); //交换
		x /= 2; //向上走
	}
}

//下移
void down(int x) { //O(log n)（大根堆反过来）
	int t = x;
	if(x * 2 <= size && heap[t] > heap[x * 2]) t = 2 * x; //若左儿子存在且小于父节点，记录
	if(x * 2 + 1 <= size && heap[t] > heap[x * 2 + 1]) t = 2 * x + 1; //若右儿子存在且小于父节点，记录
	if(t != x) { //若子节点满足条件
		swap(heap[t], heap[x]); //交换
		down(t); //向下走
	} 
}

7.Hash表

哈希表也叫散列表，是一种数据结构，它提供了快速的插入操作和查找操作，无论哈希表总中有多少条数据，插入和查找的时间复杂度都近似为 $O (1)$ ，因为哈希表的查找速度非常快，所以在很多程序中都有使用哈希表，例如拼音检查器。

哈希表也有自己的缺点，哈希表是基于数组的，我们知道数组创建后扩容成本比较高，所以当哈希表被填满时，性能下降的比较严重。

哈希表采用的是一种转换思想，其中一个重要的概念是如何将「键」或者「关键字」转换成数组下标。就比如普通数组的下标是 int 类型的，但哈希表可以把 string 类型的转换成下标。

用于转换的函数就是哈希函数，比如一个哈希函数 $h (x) (- 10^{9} \leq x \leq 10^{9}) \in [0, 10^{5}]$ 这个区间内就可以把 $- 10^{9} \sim 10^{9}$ 的所有数映射到 $[0, 10^{5}]$ 这个区间内。

哈希函数通常形式： $h (x) = x \mod N$ （ $N$ 一般是一个质数，且远离 $2$ 的幂，因为这样做可以使哈希冲突尽量小）

但是这样会有一个问题，在映射时可能会出现两个不同的数映射成同一个下标，这种情况被称为哈希冲突。哈希冲突是不可避免的，解决方法有两种：

1.拉链法
2.开放寻址法

下面就分别讲一下两种方法。

拉链法顾名思义，就是把冲突的数在此下标处拉一条链表来记录。

比如 $h (11) = h (23) = 3$ 时，如图所示：

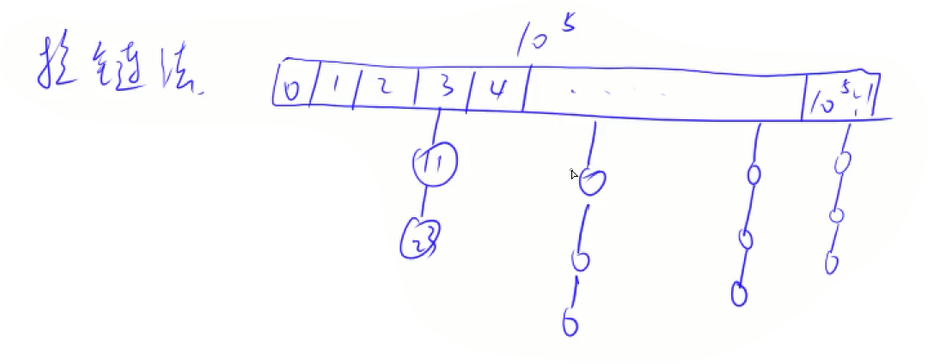
代码：

int h[N], e[N], ne[N], idx;

void insert(int x) {
	int k = (x % N + N) % N; //防止当x为负数时模出来为负
	e[idx] = x, ne[idx] = h[k], h[k] = idx++; //链表的插入操作
}

bool find(int x) {
	int k = (x % N + N) % N;
	for(int i = h[k]; i != -1; i = ne[i]) { //遍历链表1
		if(e[i] == x) return true; //找到
	}
	return false;  //未找到
}

开放寻址法

只开一个一维数组，但长度要开到 $2 \sim 3$ 倍。

插入：若 $h (x) = k$ ，那么接下来就和找位置一样，从第 $k$ 个位置开始找，如果已经被占用就往后找直到找到一个空位，再把 $x$ 放入。

查找：从下标 $k$ 开始查找，看该位置是否被占用，若被占用且为 $x$ ，则找到；如被占用但不是 $x$ ，就再看下一个位置；若未被占用，则 $x$ 不存在。

删除：按照查找的方式找到 $x$ ，再在数组里打一个标记，表示 $x$ 被删除。

代码：

int find(int x) {
	int k = (x % N + N) % N;
	
	while(h[k] != null && h[k] != x) {
		k++;
		if(k == n) k = 0; //循环看第一个位置
	}
	return k; //若未被占用则表示x应该放的位置，若找到则表示x的位置
}

字符串哈希方式：字符串前缀哈希法。

举个例子：字符串 $ABCD$ ，则它对应的哈希表:

h[0] = 0;
h[1] = "A"的hash值
h[2] = "AB"的hash值
h[3] = "ABC"的hash值
h[4] = "ABCD"的hash值

它们的 hash 值该怎么求?其实把每一个字符串看成是一个 $p$ 进制数，比如 $ABCD$ 就相当于 $p$ 进制数 $1234$ ，值为 $1 \times p^{3} + 2 \times p^{2} + 3 \times p^{1} + 4 \times p^{0}$ ，这样就把一个字符串转化成了一个数字，然后再模一个 $Q$ ，就可以把它映射在 $0 \sim Q - 1$ 之间的数了。

注：

1.不能将字母映射成 $0$ ！否则 $A$ 和 $AA$ 都是 $0$ 了！

2.~~我们人品足够好，不会发生冲突~~当 $P = 131$ 或 $13331$ ， $Q = 2^{64}$ 时，发生冲突的概率最小。

当我们知道 $h [R]$ 和 $h [L]$ 时， $L \sim R$ 段的 hash 值又为多少呢？

不妨先画个图：

由图可知，想要求出 $L \sim R$ 段的 hash 值，要将 $h [R]$ 与 $h [L]$ 对位相减，所以得出： $L \sim R$ 段的 hash 值为 $h [R] - h [L - 1] \times p^{R - L + 1}$

所以在对一个字符串的 hash 值进行预处理时可以：

h[0] = 0; //千万不要忘记！
for(int i = 1; i < len; i++) {
	h[i] = h[i - 1] * p + str[i];
}

模板题：P3370 【模板】字符串哈希

7.STL 容器的使用

1.vector

变长数组，使用了倍增的思想。

头文件：#include <vector>

2.string

字符串，substr(), c_str()

3.queue,priority_queue

队列，push(), front(), pop()

4.stack

栈，push(), top(), pop()

5.deque

双端队列

6.set, map, multiset, multimap

基于平衡二叉树（红黑树），动态维护有序序列。

7.unordered_map, unordered_set, unordered_multimap, unordered_multimap

哈希表

8.bitset

压位

posted @ 2023-09-26 15:41 Brilliant11001 阅读(8) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· 数据结构复习

· NOIP 冲刺之——数据结构

· 第二章数据结构三

· 数据结构进阶

· 【数据结构】并查集（1）萌新的并查集学习之路

阅读排行：
· 地球OL攻略 —— 某应届生求职总结
· 周边上新：园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源！
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】

Brilliant11001

一只会咬人的氯化氢~

数据结构复习2

5.并查集

P3367 【模板】并查集

6.堆

总结得太全面啦！

7.Hash表

字符串哈希方式：字符串前缀哈希法。

注：

由图可知，想要求出 $L \sim R$ 段的 hash 值，要将 $h [R]$ 与 $h [L]$ 对位相减，所以得出： $L \sim R$ 段的 hash 值为 $h [R] - h [L - 1] \times p^{R - L + 1}$

模板题：P3370 【模板】字符串哈希

7.STL 容器的使用

1.vector

2.string

3.queue,priority_queue

4.stack

5.deque

6.set, map, multiset, multimap

7.unordered_map, unordered_set, unordered_multimap, unordered_multimap

8.bitset

公告

我的标签

合集

随笔分类

Brilliant11001

一只会咬人的氯化氢~

数据结构复习2

5.并查集

P3367 【模板】并查集

6.堆

总结得太全面啦！

7.Hash表

字符串哈希方式：字符串前缀哈希法。

注：

由图可知，想要求出 L∼R 段的 hash 值，要将 h[R] 与 h[L] 对位相减，所以得出：L∼R 段的 hash 值为 h[R]−h[L−1]×pR−L+1

模板题：P3370 【模板】字符串哈希

7.STL 容器的使用

1.vector

2.string

3.queue,priority_queue

4.stack

5.deque

6.set, map, multiset, multimap

7.unordered_map, unordered_set, unordered_multimap, unordered_multimap

8.bitset

公告

我的标签

合集

随笔分类

由图可知，想要求出 $L \sim R$ 段的 hash 值，要将 $h [R]$ 与 $h [L]$ 对位相减，所以得出： $L \sim R$ 段的 hash 值为 $h [R] - h [L - 1] \times p^{R - L + 1}$