数据结构复习

大纲：

1.链表

• 单向链表

它是一种由节点构成的数据结构，每个节点都有对应的值和一个指向下一个点的指针，就像用链子串联起来一样。

如图所示：

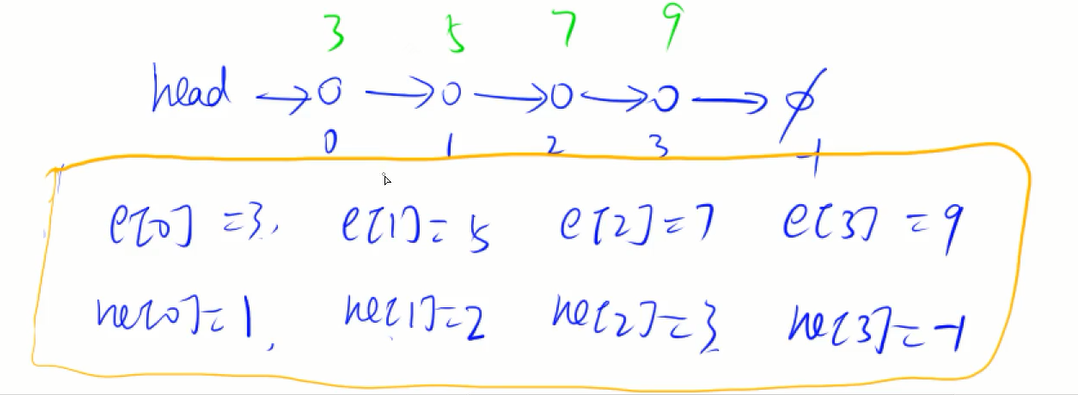
用数组模拟单向链表需要如下定义：

int head, e[N], ne[N], idx;
//head是头指针，初始指向空，e[i]表示第i个插入的点的值，ne[i]表示第i个插入
的点的下一个点的下标，idx记录现在插入了几个点

以下是各种简单操作：

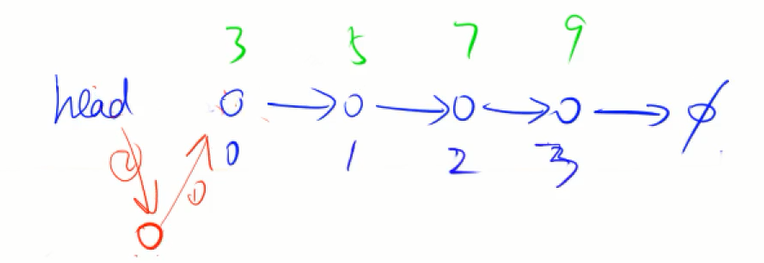
//在第a个节点插入b
void add(int a, int b) {
	e[idx] = b, ne[idx] = ne[a], ne[a] = idx++;
}

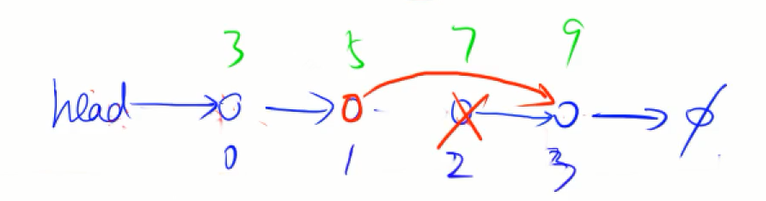
//删除第k个节点的后面的节点
void remove(int k) {
	ne[k] = ne[ne[k]];
}

//查询第k个节点后的节点
void find(int k) {
	cout << e[ne[k]] << endl;
}

B3631 单向链表

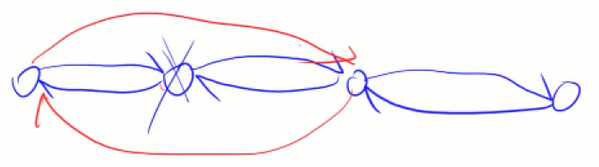
• 双向链表

单向链表的升级版，每个节点有两个指针，一个指向前节点，一个指向后节点；

如图所示：

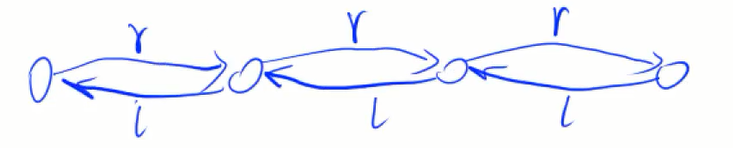
以下是各种简单操作：

//初始化
void init() {
	r[0] = 1, l[1] = 0;
	idx = 2;
}

//在第k个节点的后面插入x
void add(int k, int x) {
    e[idx] = x;
    l[idx] = k;
    r[idx] = r[k];
    l[r[k]] = idx; //必须先这一步再修改r[k]
    r[k] = idx;
}

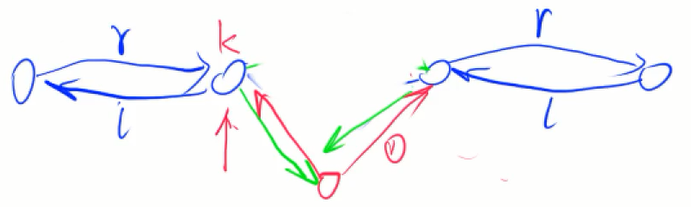
//删掉第k个节点
void remove() {
    r[l[k]] = r[k];
    l[r[k]] = l[k];
}

2.栈、队列

栈：先进先出。

队列：后进后出。

（由于对这两个数据结构的基础再熟悉不过了，其实每天都在复习，所以就不妨放在这里了，直接讲进阶知识）

单调栈

P5788 【模板】单调栈

本蒟蒻认为它和单调队列都比较抽象

对于这个问题如果采用暴力做法，写两层循环，则在最坏情况的时间复杂度为 \(O(n^2)\)，效率较低，我们来考虑优化。会发现，在这个序列中，如果一个数右边的数小于等于它，那么它就无论如何都不能被当作答案输出了，所以这时它已经没有任何作用了，就把它删掉。（也可以理解为一个长得高的人向右看不容易看到比他矮的人，而会先看到比他高的人）我们把每一个逆序数都删掉后，这个序列就变成了一个单调序列，在此是单调递增的。

如图所示：

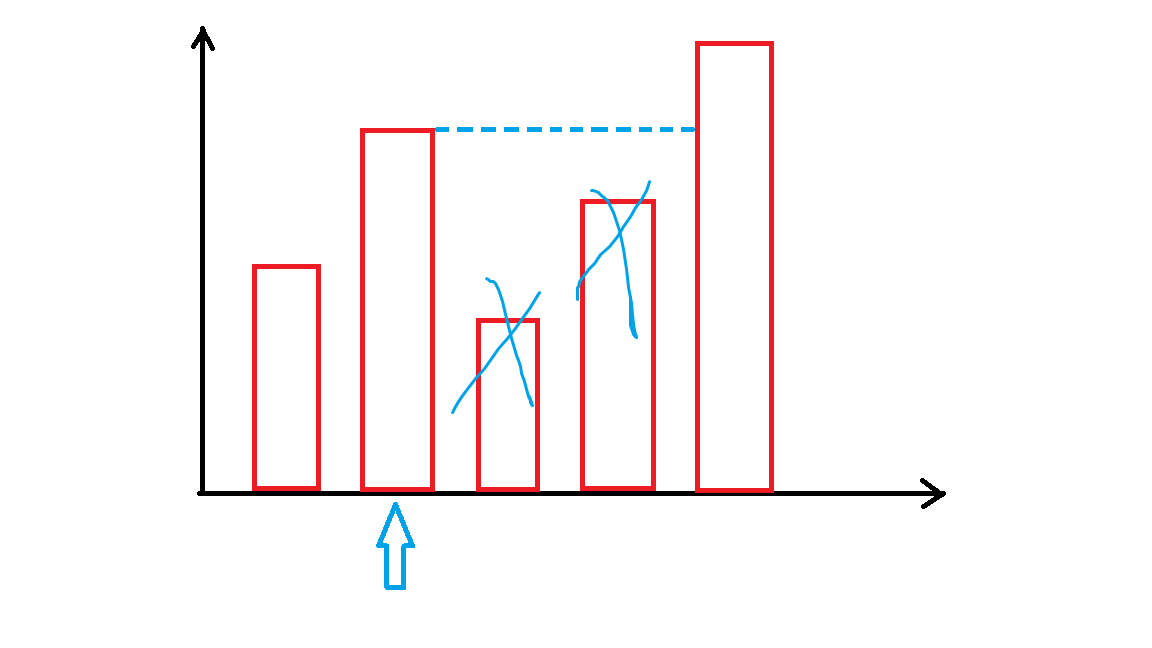
然后又因为删除时是从前面弹出，这和栈结构十分相似，所以称之为单调栈。

如图所示：

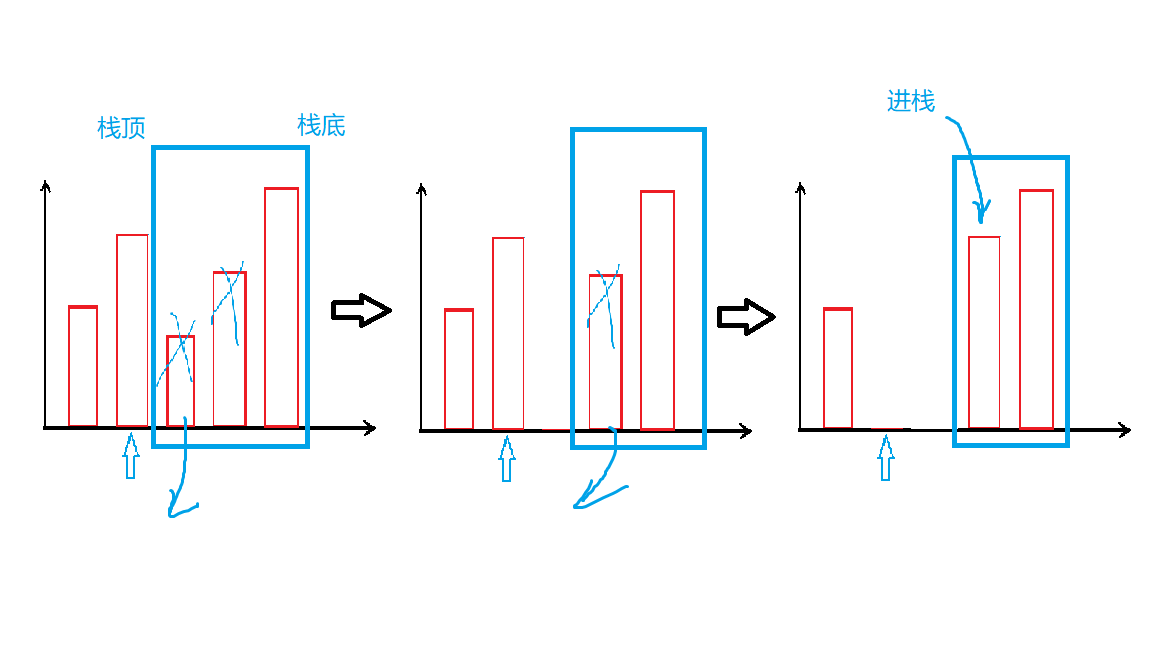
代码：

#include <iostream>
using namespace std;
const int N = 3000010;
long long n, tt, a[N], stk[N], ans[N];
int main() {
	cin >> n;
	for(int i = 1; i <= n; i++) cin >> a[i];
	for(int i = n; i >= 1; i--) {
		while(tt > 0 && a[stk[tt]] <= a[i]) tt--;//如果栈不空且
        栈顶下标对应的数比当前的数小，就没用了，弹出
		ans[i] = stk[tt];//由于这道题要求输出下标并倒序输出，所以将下标作为栈中元素并记录在数组中
		stk[++tt] = i;//将当前下标进栈
	}
	for(int i = 1; i <= n; i++) cout << ans[i] << " ";
	return 0;
}

单调队列

和单调栈原理差不多，一般用来解决滑动窗口中的最大最小值问题，可用来优化多重背包。

P1886 滑动窗口 /【模板】单调队列

如果采用暴力做法，对窗口里的数进行遍历，遍历n次，那么时间复杂度为 \(O(nk)\)，对于 \(1\le k\le n\le 10^6\)的数据范围，会直接 TLE。

我们来考虑优化。先考虑最小值，以样例为例，当窗口滑动到如下位置时，\(-3\) 进入窗口，因为 \(-3\) 比它们都小且排在他们后面，只要-3在窗口中，那么 \(3\) 和 \(-1\) 永远都不可能被当作答案输出，此时 \(3\) 和 \(-1\) 都没用了，将它们删掉。会发现先进入窗口的先被删掉，和队列结构十分相似。

按照这样的方法，把序列中所有的逆序数删完后，整个序列变成了一个单调序列，这里是单调递增。那么求最小值就简单了，其实就是队首的值。求最大值反过来就行了。

代码：

#include <iostream>

using namespace std;
const int N = 1000010; 
int hh, tt = -1, q[N], n, k;
int a[N];

int main() {
	cin.tie(0);
	cin >> n >> k;
	for(int i = 1; i <= n; i++) cin >> a[i];
	for(int i = 1; i <= n; i++) {
		//判断队头是否滑出窗口，队中存下标 
		if(hh <= tt && i - k + 1 > q[hh]) hh++;
		while(hh <= tt && a[q[tt]] >= a[i]) tt--; //若队尾大于当
        					前的数，则队尾没用，删去 
		
		q[++tt] = i; //先将当前的数的下标放入队列再输出，否则可
        		能a[i]太小将队列清空，输出的就是不明所以的东西了 
		if(i >= k) cout << a[q[hh]] << " "; //因为窗口的左端点是
        		从第一个数开始的，所以要特判从第k位开始输出 
	}
	return 0;
}

3.KMP字符串匹配大法

这位更是重量级，第一次学时根本听不懂，太抽象了

P3375 【模板】KMP 字符串匹配

朴素算法的话就是写两层循环，将母串一位一位往后推，一次一次地从字串头开始匹配，若不匹配就 break 掉。但是这样时间复杂度为 \(O(n^2)\)，效率较低。

怎么优化呢？其实我们发现，按照朴素做法，在某一次匹配失败后字串将向后移一位，但是其实已经匹配了很多位了，不需要再从头开始。

如图所示：

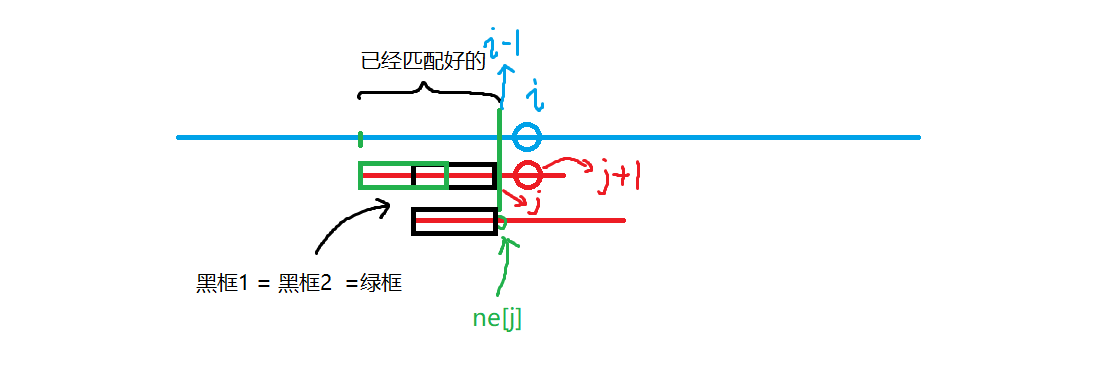
假设母串匹配到第 \(i\) 位时发现与子串的第 \(j + 1\) 位不匹配了，那么我们将子串向后平移，直到又可以继续匹配，这时就需要满足黑框 \(1 =\) 黑框 \(2 =\) 绿框，也就是在子串的某一段中存在前缀等于后缀，且相等的部分最长，这样就可以得到子串向后平移的最小长度。如果我们一开始就对这个子串进行一次这样的预处理，将开头到子串中各个位置都求出前缀等于后缀时的最长长度，那么在匹配失败时就可以精准地跳到下一个可以匹配的地方。

怎么实现呢？定义一个数组 \(next[N]\)，\(next[i] = j\) 表示母串 \(p\) 中 \(p[1\sim j]\) 前缀等于后缀时的最长长度，即此时 \(p[1\sim j] = p[i - j + 1\sim i]\)。

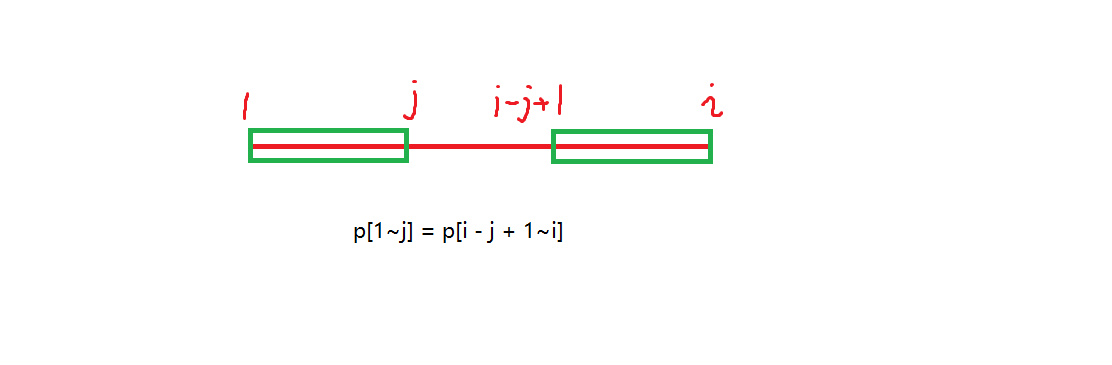
现在的问题就是怎么求出这个数组。其实这是个递推的过程，假设我们求到了 \(next[i]\)，这时 \(p[i] != p[j + 1]\)，由于黑框部分也存在前后缀相等（若不存在则 \(next[j] = 0\)，直接跳到开头），就是这里的绿框相等，由于所有的黑框都是相等的，所以所有的绿框都是相等的，这里 \(next[j]\) 代表的就是绿框的长度。这时只需要比较 \(next[j]\) 后面一位与 \(p[i]\) 是否相等就行了，若相等则 \(next[i] = ne[j] + 1\)，\(i++\), 若不相等则再取 \(next\) 值，也就是 \(next[next[j]]\)。简单来说就是若匹配成功了就前进一步，若失败就退而求其次，退到 \(next[j]\)。

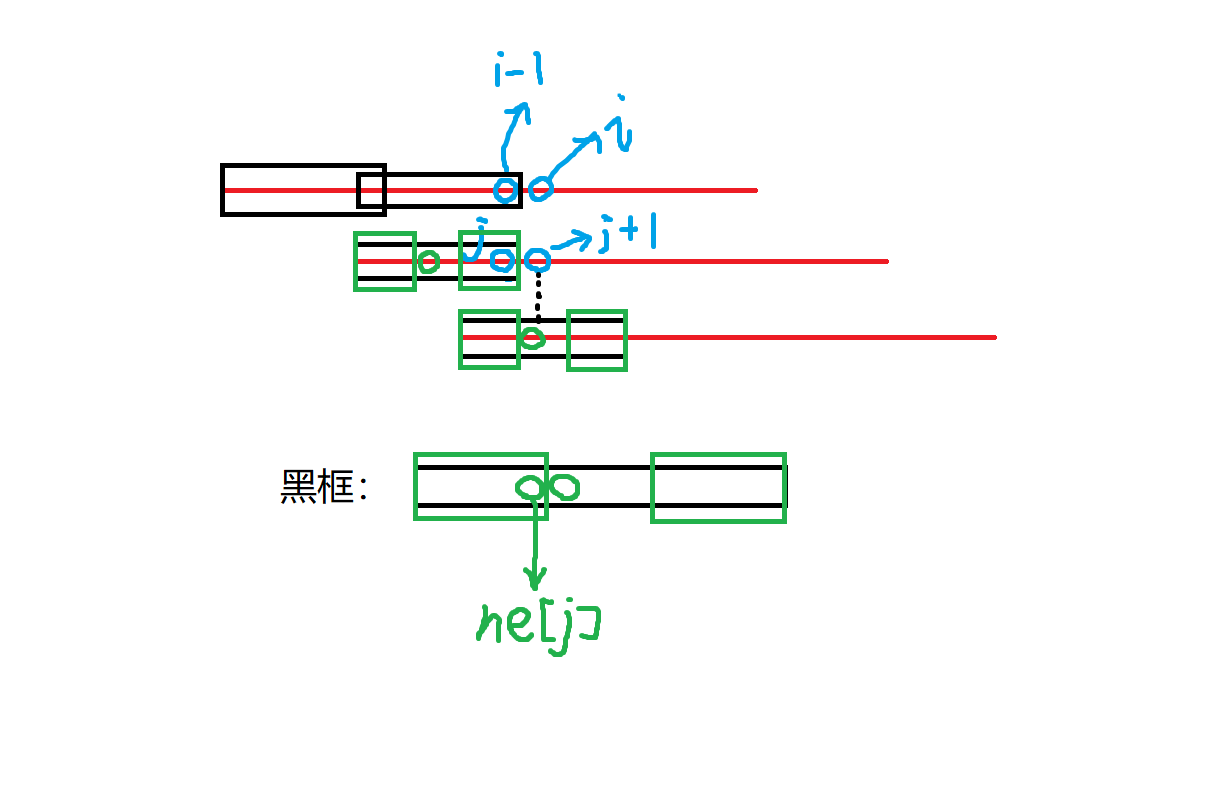
代码：

#include <iostream>
#include <cstring> 
using namespace std;
const int N = 1000010;
int lens, lenp, ne[N];
char s[N], p[N];
int main() {
	cin.tie(0);
	cin >> s + 1 >> p + 1; //下标从1开始
	lens = strlen(s + 1), lenp = strlen(p + 1);
	
	//求next数组
	for(int i = 2, j = 0; i <= lenp; i++) {
		while(j && p[i] != p[j + 1]) j = ne[j]; //若还能退且失配
        						，则退而求其次 
		if(p[i] == p[j + 1]) j++; //若匹配了，则前进一步 
		ne[i] = j; //记录 
	} 
	
	//KMP匹配过程
	for(int i = 1, j = 0; i <= lens; i++) {
		while(j && s[i] != p[j + 1]) j = ne[j]; //若还能退且失配，则退而求其次 
		if(s[i] == p[j + 1]) j++; //若匹配了，则前进一步 
		if(j == lenp) { //匹配成功
			cout << i - lenp + 1 << endl;
			j = ne[j]; //继续退，寻找其他匹配成功的情况 
		}
	} 
	for(int i = 1; i <= lenp; i++) {
		cout << ne[i] << " ";
	}
	return 0;
}

4.\(\texttt{trie}\) 树（字典树）

\(\texttt{trie}\) 是一个高效的地储存和查找字符串集合的数据结构。顾名思义，它是一个树形结构，那么它是如何做到高效的地储存和查找字符串集合的呢？

如图所示：

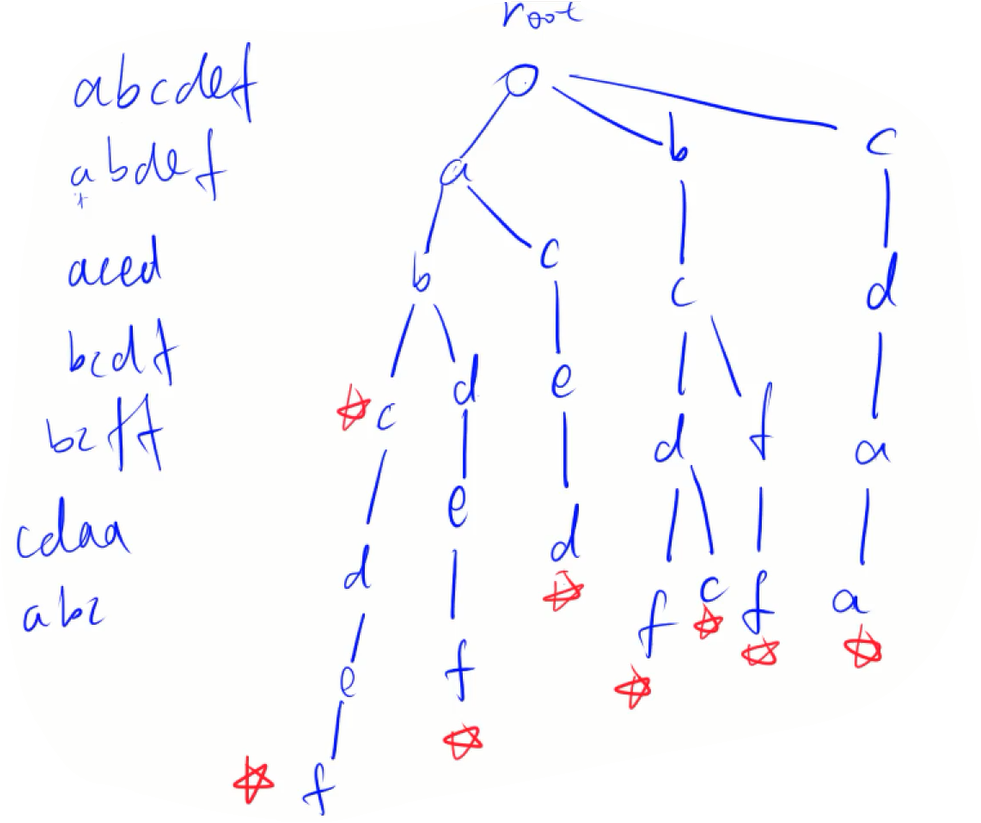
比如插入第一个字符串 \(\texttt{abcdef}\)，先从根节点出发，发现它没有字符 \(a\) 这个子节点，于是就创建一个子节点 \(a\)，然后走到 \(a\) 节点，发现它没有字符 \(b\) 这个子节点，于是就创建一个子节点 \(b \dots\dots\) 以此类推，直到整个字符串都储存好，在最后的一个节点上打上一个标记（原因等会儿就讲），表示存在一个字符串由此字符结尾。

再看第二个字符串 \(\texttt{abdef}\)，同样从根节点出发，发现有字符 \(a\) 这个子节点， 于是直接走过去，又发现有字符 \(b\) 这个子节点，再走过去，发现没有字符 \(d\) 这个子节点，于是就创建一个子节点 \(d \dots\dots\) 按照这样的顺序将所有的字符串都储存好，就形成了一棵由字符构成的树。

再比如我要查找是否存在字符串 \(\texttt{bcdf}\)，从根节点开始，发现存在节点 \(b\)，走过去，发现节点 \(c\) 也存在，最后发现所有的字符都存在，且节点 \(f\) 处有结束标记，所以该字符串存在。

假如我要查找字符串 \(\texttt{acef}\) 是否存在，按照刚刚的操作会发现 \(e\) 节点无 \(f\) 子节点，所以该字符串不存在。

再假如我要查找字符串 \(\texttt{ace}\) 是否存在，操作后虽然所有字符都有记录，但 \(e\) 节点处没有结束标记，所以该字符串不存在。这就是为什么要打结束标记。

问题来了，该怎么实现？

首先我们得先把所有的字符映射成数字，代码如下：

//映射字符
int mapping(char c) { //0~25是小写字母，26~51是大写字母，52~61是数字0~9
	if(c >= 'A' && c <= 'Z') {
		return c - 'A';
	}
	else if(c >= 'a' && c <= 'z') {
		return c - 'a' + 26;
	}
	else return c - '0' + 52; 
}

然后定义数组 \(trie[N][65]\) 来储存这个树，\(cnt[N]\) 来储存以每个节点结尾的字符串的个数，同时也就起到了打标记的作用，还有 \(idx\) 来表示用到了哪个下标。

int trie[N][65], cnt[N], idx;

各种简单操作：

//插入一个字符串
void insert(char str[]) {
	int p = 0; //从根节点开始
	for(int i = 0; str[i]; i++) {
		int u = mapping(str[i]); //映射字符
		if(!trie[p][u]) trie[p][u] = ++idx; //若无此子节点，添加
		p = trie[p][u]; //走过去
	}
   cnt[p]++; //以该末尾字符结尾的字符串又多了一个
}

//查询某个字符串的出现次数
int query(char str[]) {
	int p = 0;
	for(int i = 0; str[i]; i++) {
		int u = mapping(str[i]);
		if(!trie[p][u]) return 0; //如果有一个字符不同就不存在
		p = trie[p][u];
	}
	return cnt[p]; //返回出现次数
}

废话不多说，直接上模板题。

P8306 【模板】字典树

这道题还有点不同，是看作为前缀的出现次数，但其实比较简单，只需要将插入函数改成这样：

void insert(char str[]) {
	int p = 0;
	for(int i = 0; str[i]; i++) {
		int u = mapping(str[i]);
		if(!trie[p][u]) trie[p][u] = ++idx;
		p = trie[p][u];
		cnt[p]++; //移到循环内部，表示有多少个字符串经过它
	}
}