搜索与图论（3）最小生成树 && 二分图
知识大纲
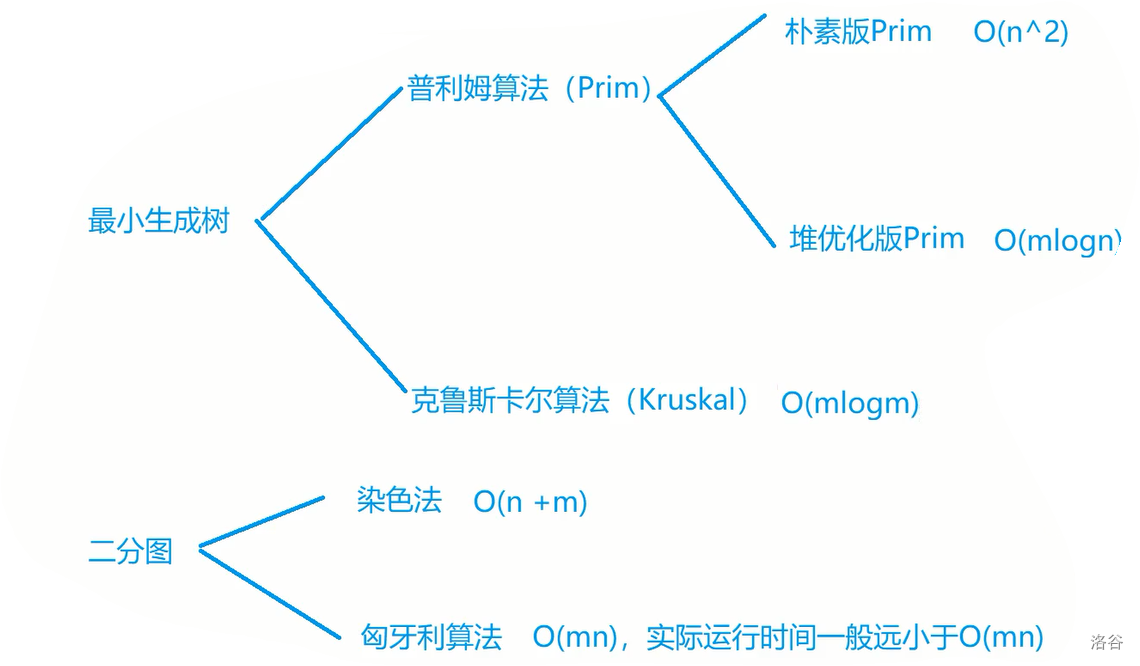
对于最小生成树，若是稠密图则用朴素版 Prim 算法，若是稀疏图则用 Kruskal 算法，因为思路很简单，代码也比较简洁。
对于二分图，判断二分图用染色法，求二分图的最大匹配用匈牙利算法。
最小生成树
定义：一个有 \(n\) 个结点的连通图的生成树是原图的极小连通子图，且包含原图中的所有 \(n\) 个结点，并且有保持图连通的最少的边。
简单来说，就是保留了一个图的所有结点，且连接每个节点的边权之和最小。
如下图：
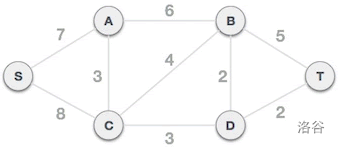
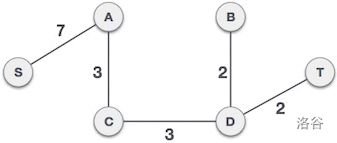
1. Prim 算法
和 Dijkstra 算法有异曲同工之妙
朴素版
总体思路：
这里的集合 \(s\) 是指已经被放入连通图的所有节点。需要提到一点，到集合的距离定义为所有与集合中节点相连的边的中的最小值，具体来说如下图：
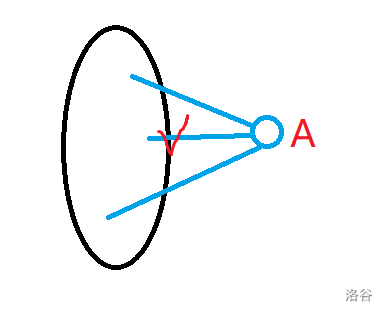
中间那条边就是节点到集合的距离。
代码：
int prim() {
memset(dist, 0x3f, sizeof dist);
int res = 0; //最小生成树的边权值和
for(int i = 0; i < n; i++) {
int t = -1;
for(int j = 1; j <= n; j++) {
if(!st[j] && (t == -1 || dist[j] < dist[t])) t = j; // 找最小值
}
if(i && dist[t] == INF) return INF; //若不是第一个点且到
集合的距离为正无穷，说明所有的点不连通，无最小生成树
if(i) res += dist[t]; //累加权值（必须先累加，再更新，否
则假如有自环，t会把自己更新）
for(int j = 1; j <= n; j++) dist[j] = min(dist[j], g[t][j]);
//dist[j]表示的是j到集合的距离（未确定），g[t][j]是集合中某点到
j的距离
st[t] = true; //放入集合
}
return res;
}
堆优化版
不常用，和 Dijkstra 算法的堆优化版优化的地方相同，都是找最小值的地方。
代码：
typedef pair<int, int> PII;
……
int Prim()
{
memset(vis, false, sizeof vis);
memset(dist, 0x3f, sizeof dist);
int sum = 0, cnt = 0; //sum记录总权值，cnt记录集合中点的个数
priority_queue<PII, vector<PII>, greater<PII>> q;
q.push({0, 1});
while (!q.empty()) {
PII t = q.top();
q.pop();
int ver = t.second, dst = t.first;
if (vis[ver]) continue; //已加入，跳过
vis[ver] = true, sum += dst, ++cnt; //加入集合
for (int i = h[ver]; i != -1; i = ne[i]) {
int j = e[i];
if (!vis[j] && w[i] < d[j]) { 加入堆中的起码要比之前更新的到
生成树的距离要小，这样就可以减少很多条边入堆
d[j] = w[i];
q.push({w[i], j});
}
}
}
if (cnt != n) return INF; //若集合中节点不为n，则说明不连通，无最小生成树
return sum;
}
2.Kruskal 算法
一个优雅的算法 \(\sim\)
总体思路：
代码：
void kruskal() {
for(int i = 1; i <= n; i++) p[i] = i; //初始化并查集
int res = 0, cnt = 0; //res存权重和，cnt存加了多少条边
for(int i = 1; i <= m; i++) { //从小到大遍历所有边
int a = edge[i].a, b = edge[i].b, w = edge[i].w;
a = find(a), b = find(b); //找祖先
if(a != b) { //如果不连通，则连边
p[a] = b; //将两个集合合并
res += w;
cnt++;
}
}
if(cnt < n - 1) puts("impossible"); //若加的边小于n - 1条，则不连通
else printf("%d\n", res);
}
二分图
二分图又称作二部图，是图论中的一种特殊模型。
定义： 设 \(G = (V ,E)\) 是一个无向图，如果顶点 \(V\) 可分割为两个互不相交的子集 \((A,B)\) ，并且图中的每条边 \((i，j)\) 所关联的两个顶点 \(i\) 和 \(j\) 分别属于这两个不同的顶点集 \((i, j)\) ，则称图 \(G\) 为一个二分图。
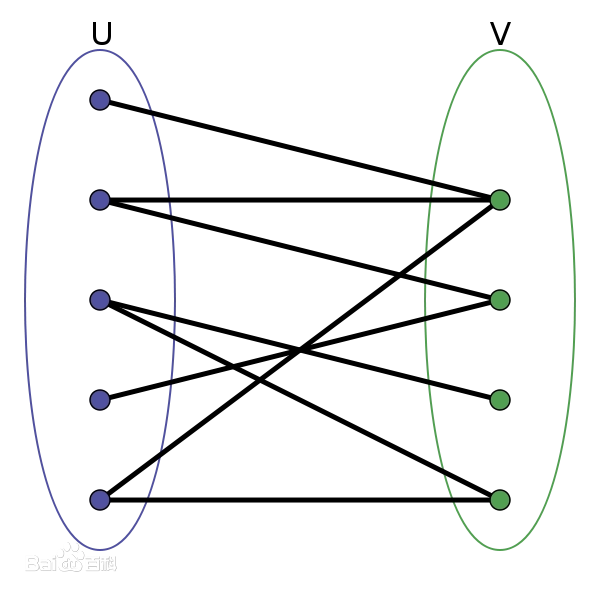
百度百科上的，太抽象了本蒟蒻根本看不懂
按照我自己的理解就是有一个图，假如它的节点能被划分成两个集合，且这两个集合中没有边，所有的边都在两个集合之间，那么这个图就是二分图。
那我们怎么判断一个图是不是二分图呢？百度百科又来了：
无向图 \(G\) 为二分图的充分必要条件是， \(G\) 至少有两个顶点，且其所有回路的点数均为偶数（不含奇数环）。
怎么证明呢？我们要证明充分必要条件，那就分别证明充分性和必要性。
充分性：
要证明充分性，即证明当图中不含奇数环时，染色是没有矛盾的。
反证法：假设染色过程中有矛盾，那么矛盾一定是在染色时发现两个被染过的相邻节点颜色相同，如下图：
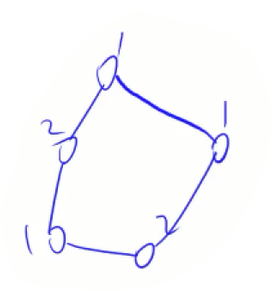
容易看出，此时构成了奇数环，所以当图中不含奇数环时，染色是没有矛盾的。
必要性：
假如一个回路的点数为奇数，如图所示：
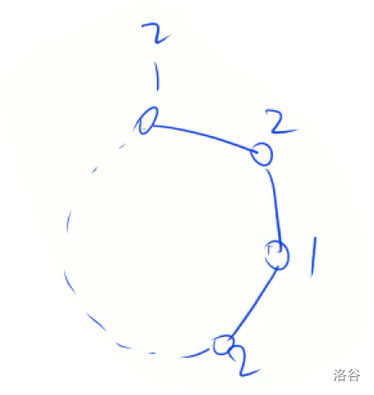
反证法：假设这是个二分图，令最上面那个点属于集合 \(1\) ，所以它的相邻点（右边的点）就应该属于集合 \(2\) ，所以第 \(3\) 个点就应该属于集合 \(1\) ，以此类推 \(\dots\dots\) 因为点数为奇数，所以当我们绕一圈推回来就会发现第一个点应该属于集合 \(2\) 这就与之前相矛盾了，所以假设不成立，它不是二分图。
染色法代码实现：
深搜：
bool dfs(int u, int c) { //颜色为1或2
color[u] = c; //给节点u染上颜色c
for(int i = h[u]; i != -1; i = ne[i]) { //遍历每一个与其相邻的点
int j = e[i];
if(!color[j]) { //若没染过色，就染色
if(!dfs(j, 3 - c)) return false; //若接下来的染色过程中有矛盾，则失败
}
else if(color[j] == c) return false; //若相邻节点颜色相同，则矛盾，失败
}
return true; //若无事发生，则成功
}
广搜：
bool bfs() {
queue <int> q;
int color[N] = {0};
for(int i = 1; i <= n; i++) {
if(!color[i]) {
q.push(i);
color[i] = 1;
while(!q.empty()) {
int t = q.front();
q.pop();
for(int j = h[t]; j != -1; j = ne[j]) {
int k = e[j];
if(!color[k]) {
q.push(k);
color[k] = 3 - color[t];
}
else if(color[k] == color[t]) return false;
}
}
}
}
return true;
}
P1330 封锁阳光大学
P1525 [NOIP2010 提高组] 关押罪犯
二分图最大匹配（匈牙利算法）
二分图的匹配：给定一个二分图 \(G\)，在 \(G\) 的一个子图 \(M\) 中，\(M\) 的边集 \({E}\) 中的任意两条边都不依附于同一个顶点，则称 \(M\) 是一个匹配。
简单来说，就是若一个节点最多只连一条边，就叫一个匹配。
二分图的最大匹配：所有匹配中包含边数最多的一组匹配被称为二分图的最大匹配，其边数即为最大匹配数。
通俗一点讲就是：一张桌左右两旁分别有 \(n1\) , \(n2\) 个男生，妹子。然后看看最多能有多少对在一起了。
基本思路：
如果你想找的妹子已经有了男朋友，
你就去问问她男朋友，
你有没有备胎，
把这个让给我好吧
多么真实而实用的算法
代码如下：
#include <iostream>
#include <cstring>
using namespace std;
const int N = 510, M = 100010;
int n1, n2, m;
int h[N], ne[M], e[M], idx;
bool st[N];
int match[N];
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
int find(int x) {
//遍历自己喜欢的女孩
for(int i = h[x] ; i != -1 ;i = ne[i]) {
int j = e[i];
if(!st[j]) {//如果在这一轮模拟匹配中,这个女孩尚未被预定
st[j] = true;//那x就预定这个女孩了
//如果女孩j没有男朋友，或者她原来的男朋友能够预定其它喜欢的女孩。配对成功
if(!match[j]||find(match[j])) {
match[j] = x;
return true;
}
}
}
//自己中意的全部都被预定了。配对失败。
return false;
}
int main() {
memset(h, -1, sizeof h);
cin >> n1 >> n2 >> m;
while(m--) {
int a,b;
cin >> a >> b;
add(a, b);
}
int res = 0;
for(int i = 1; i <= n1 ;i++) {
//因为每次模拟匹配的预定情况都是不一样的所以每轮模拟都要初始化
memset(st, false, sizeof st);
if(find(i)) res++;
}
cout << res << endl;
return 0;
}
