搜索与图论（1)
目录
1.深度优先搜索（DFS）
2.宽度优先遍历（BFS)
3.树与图的储存
4.树与图的深度优先遍历
5.树与图的宽度优先遍历
6.拓扑排序
1.深度优先搜索（DFS）
深搜，顾名思义，就是优先考虑搜索的深度，尽量往深了搜，就像一个执着的人，一条道走到黑。如果没有路可走了就往回退一步，继续寻找可以走的路，同时还要恢复搜索之前的一切（恢复现场），这就是回溯。
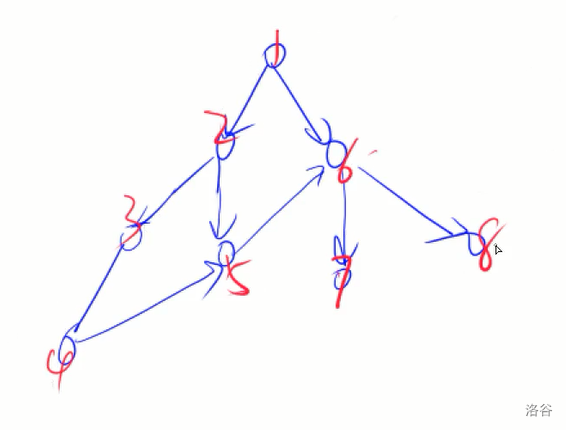
如图所示：
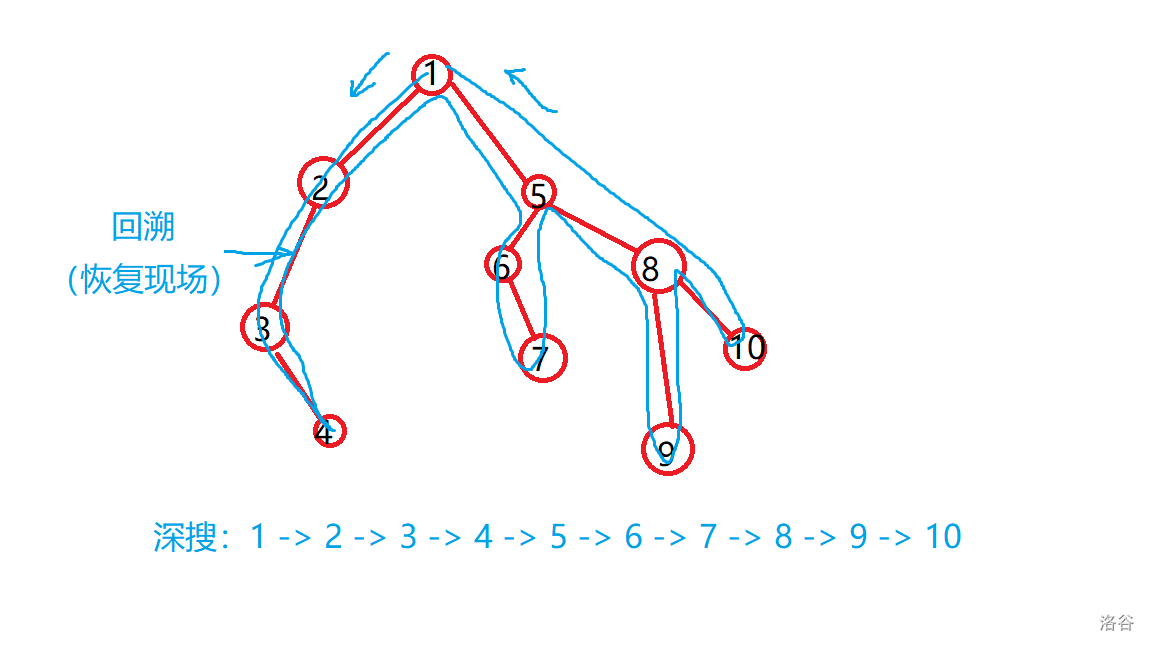
搜索轨迹看起来就像一棵树，虽然图有点丑，但确实有一点像吧。
代码实现：
void dfs(int u) {
if(u == n) { //如果搜到终点
//输出答案
return ;
}
for(int i = 1; i <= n; i++) {
if(!vis[i]) { //如果没有访问过
//记录
vis[i] = true; //标记已经走过
dfs(u + 1); //往深的一层继续搜索
//如果没路了
//撤销记录
vis[i] = 0; //恢复现场
}
}
}
------------
2.宽度优先搜索（BFS）
也叫广度优先搜索，即广搜。它的搜索顺序与深搜不同，它优先考虑的是搜索的宽度，就像一个稳重的人，先搜索下一步所有的可能，再在每种可能的基础上进行扩展，直到搜到答案。
如图所示：
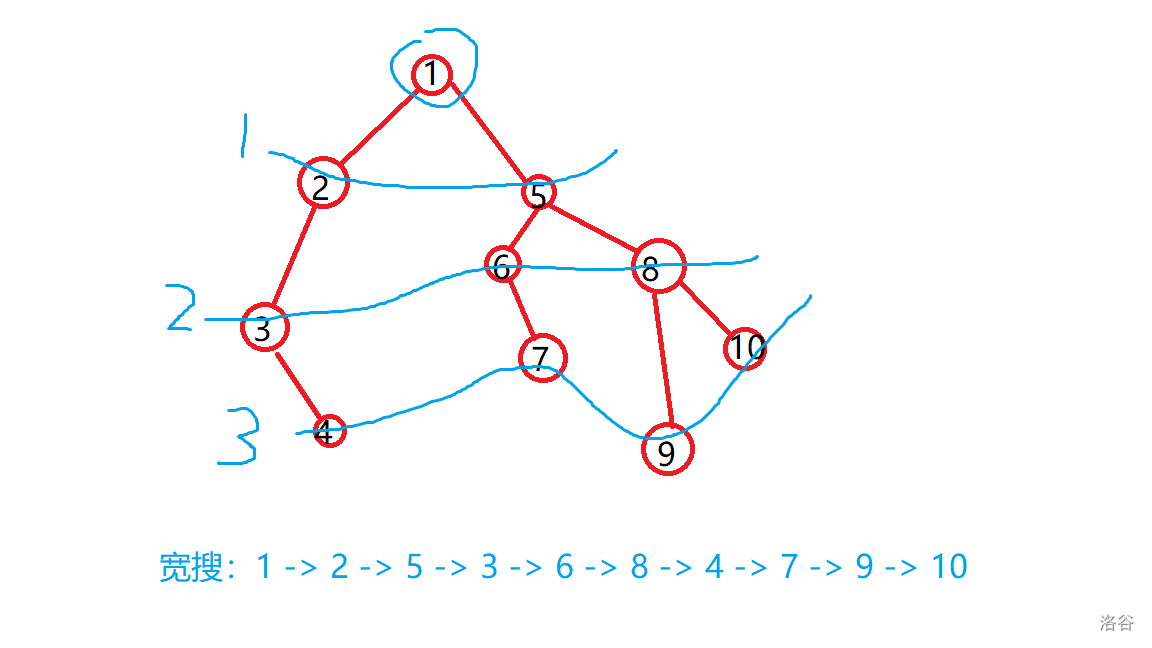
搜索轨迹看起来像水波，逐渐向远处扩散。
代码实现：
void bfs() { //宽搜
//宽搜要用队列哦
q.push(1); //压入起点
while(!q.empty()) { //若队列不空
int t = q.front(); //取出队头
q.pop(); //弹掉
if(……) { //若搜到答案
//输出答案
return ;
}
//扩展队列
}
}
还能再具体一点吗？
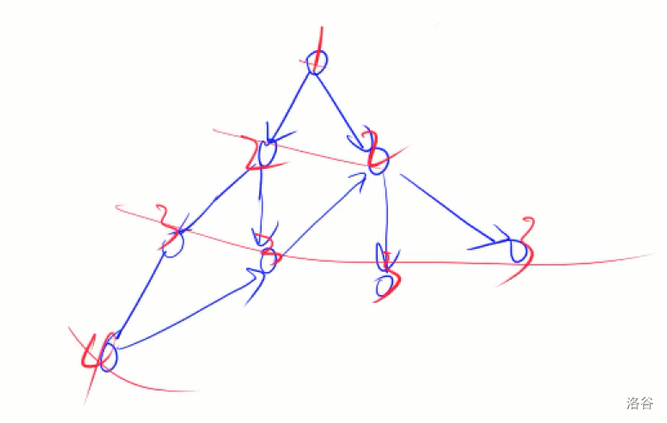
宽搜实现过程如图：
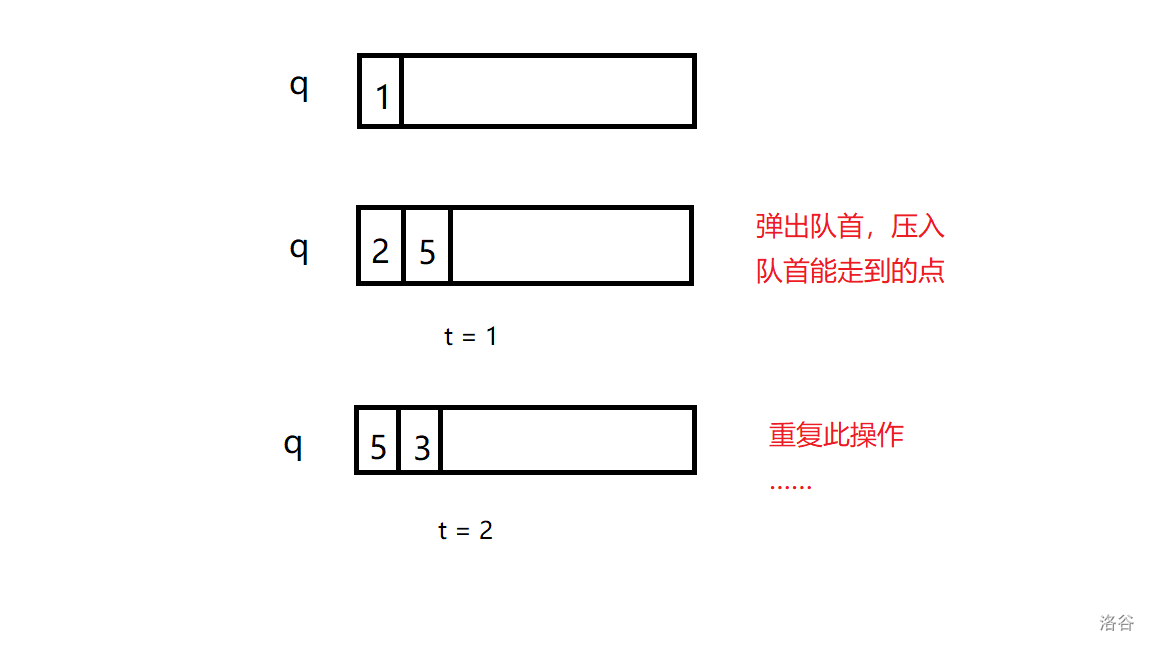
在此总结一下深搜和宽搜的区别：
深搜对应的数据结构是 stack（栈），空间复杂度 \(O(h)\) (\(h\) 为深度），时间复杂度 \(O(2^h)\) , 它不具有最短性。
宽搜对应的数据结构是 queue（队列），空间复杂度 \(O(2^h)\)，时间复杂度 \(O(h)\)，可用于求最短路（只有当边权值固定为 \(1\) 时才可用），因为在第一次搜到时必定是最短路。
3.树与图的储存
因为树是一种特殊的图（无环连通图），图分为两种，有向图和无向图，无向图又是一种特殊的有向图，所以这里我们只用考虑有向图的储存方式即可触类旁通。
有向图的存储通常有两种方式，分别为邻接矩阵、邻接表。
邻接矩阵
这是一种使用较少的方法，它的实质是定义一个二维数组用于储存这张图的信息。比如定义 \(mapp[a][b]\) 储存的是节点a到节点b的边的信息，若有权重，则储存权重；若无权重，则为一个布尔值，\(0\) 表示无边，\(1\) 表示有边。
邻接表
它的实质是对于每个节点，都定义了一个单链表，用于存储这个点可以走到哪个点。
如图所示：
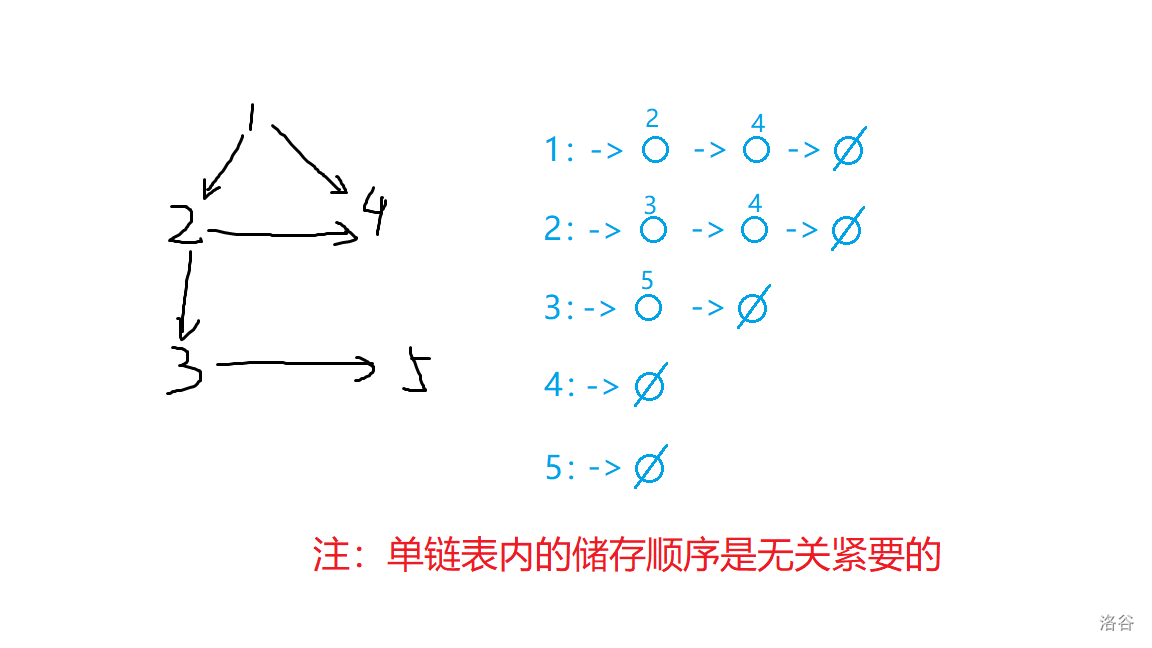
以上两种存储方式的空间复杂度都为 \(O(n^2)\) 且运行速度较慢，那有没有一个相对较快、内存占用低的方式呢？
我们将邻接表进行优化，便得到了一个新方式：链式前向星。
与普通邻接表不同，链式前向星是一个链式结构，而普通邻接表是线性结构，无论是时间上还是空间上，链式前向星都完胜普通邻接表。
那我们怎么来实现它呢？代码如下：
const int N = 10010;
int h[N], e[N], ne[N], idx; //h[N]记录每个节点的最后一条出边，e[N]记录每
条边要到达的点，ne[N]记录了从相同节点出发的下一条边在e[N]数组中的储存位置，
idx表示读到了第几条边
void add(int a, int b) { //插入一条由a指向b的边
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
这里有更加详细的介绍
4.树与图的深度优先遍历
同上，我们只考虑如何遍历有向图。实现方式和深搜类似。
时间复杂度：\(O(n + e)\)
代码实现：
void dfs(int u) { //从节点u开始
vis[u] = true; //标记已被访问过
for(int i = h[u]; i != -1; i = ne[i]) { //遍历此节点的每一条边
int j = e[i];
if(!vis[j]) dfs(j); //若未被访问，则继续深搜
}
}
5.树与图的宽度优先遍历
实现方式和宽搜类似。
时间复杂度：\(O(n + e)\)
代码实现：
int d[N]; //储存第一个节点到其他节点的距离（最小距离）
void bfs() {
q.push(1);
memset(d, -1, sizeof(d));
d[1] = 0; //第一个点到自己的距离当然为0
while(!q.empty()) {
int t = q.front();
for(int i = h[t]; i != -1; i = ne[i]) {
int j = e[i];
if(d[j] == -1) { //若第一次搜到
d[j] = d[t] + 1; //记录距离
q.push(j); //扩展队列
}
}
}
printf("%d", d[n]); //输出
}
6.拓扑排序
拓扑序列是针对有向图说的，无向图是没有拓扑序列的。它的定义是：如果一个由点组成的序列 \(A\) 满足，对于图中的每条边 \((x, y)\) ，\(x\) 在 \(A\) 中都出现在 \(y\) 之前，则 \(A\) 是该图的一个拓扑序列。
为什么说“一个拓扑序列”呢？我们不难发现，对于某些有向无环图，不只有一个拓扑排序，比如：
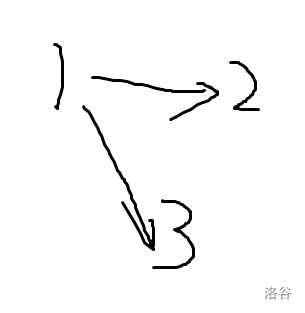
这个图就有两个拓扑序列，分别为 \(1 2 3\) 和 \(1 3 2\) 。
我们如何求一个有向无环图的拓扑序列呢？
其实需要用到上面讲的宽度优先遍历。首先我们思考，什么样的节点可以放在序列的前面呢？显然，所有入度为 \(0\) 的点都是可以作为起点的，因为没有任何一条边指向它，即没有任何一个点能在它的前面,所以我们先让所有入度为 \(0\) 的点入队，此时剩下的节点一定就为入度不为 \(0\) 的节点了，接下来又该怎么办呢？
你看，所有入度为 \(0\) 的点都已经放在前面了，假设其中有个节点 \(A\) ，有条边由 \(A\) 指向 \(B\) ，那意思是不是说， \(B\) 一定在 \(A\) 的后面？答案是肯定的，这样我们就保证了节点 \(A\) 的所有出边所连的节点都是一定满足以上规律的，既然这样，这些边对于 \(A\) 便没有任何作用了，我们将这些边删掉。删掉后，如果 \(B\) 也变成了入度为 \(0\) 的点，那又可以将 \(B\) 放入队列，以此类推。
代码实现如下：
int h[N], e[N], ne[N], idx;
int n, m, d[N];
int q[N];
void topsort() {
int hh = 0, tt = -1; //手写队列
for(int i = 1; i <= n; i++) { //所有入度为0的点入队
if(!d[i]) q[++tt] = i;
}
while(hh <= tt) {
int t = q[hh++];
for(int i = h[t]; i != -1; i = ne[i]) { //遍历队头节点的
所有出边
int j = e[i];
d[j]--; //删除此边
if(!d[j]) q[++tt] = j; //若B也变成入度为0的点，
则将B放入队列
}
}
for(int i = 0; i < n; i++) {
printf("%d ", q[i]); //输出（这里体现出了手写队列的好处，弹出操作只是将队头指针往后移动，但排好序的序列刚好是从下标0开始的，没有被“弹掉”
}
return ;
}
这时候就有有一个疑问了，这样做真的可以使这个有向无环图的所有节点入队吗？答案是可以的。我们可以浅浅地证明一下。
这里采用反证法来证明（主要是蒟蒻不知道怎么从正面证明）首先，只有入度为 \(0\) 的点才能被压入队列，假设存在一个有向无环图，我们用以上方法不能求出它的拓扑排序，则当程序进行到一定程度时找不到入度为 \(0\) 的点，且仍有点未入队。所以此时所有的节点至少有一个入边，不妨设每个节点有且仅有一条入边，我们从节点 \(A\) 开始找起，则必定有一个节点 \(B\) 指向它，那么也必定有一个节点 \(C\) 指向节点 \(B\) \(\dots\dots\) 以此类推，假设此图有 \(n\) 个节点，但我们会找出 \(n + 1\) 个点。根据抽屉原理，则必定有两个节点重合，即这两个节点为同一节点，则必然存在一个环，不合题意，故假设错误，所以对于所有的有向无环图，我们用以上方法都能求出它的拓扑排序，证明完毕。
这样一来，我们不仅证明了这个方法的可行性，还得到了一条重要性质：对于所有的有向无环图，至少存在一个入度为 \(0\) 的节点。
