Solution 题解 UVA1389 Hard Life: 最小割,有向图,分数规划,和牛顿迭代
题解 UVA1389 Hard Life: 最小割,有向图,分数规划,和牛顿迭代
Preface
黑题好耶
看到了题解里面大多数是二分,我就来讲一讲简单又快速的 Dinkelbach Algorithm 吧!
0-1 分数规划与线性规划
首先把人员看作点集\(V\),把矛盾看作边集\(E\)。
令\(V'\subseteq V\)表示被裁人员的集合,然后\(E'=\{(u,v)\in E:u,v\in V'\}\)则为被裁人员之间的矛盾。
那么我们的问题就是最大化 \(|E'|/|V'|,\) 一个及其类似 0-1 分数规划 的问题。
0-1 分数规划的最常用方法(也是很优秀的方法)是用二分答案将该问题转化为 0-1 线性规划。
在这道题中,因为我们想要最大化 \(|E'|/|V'|\),我们就给出一个目标值 \(\lambda\),并试图找到让 \(|E'|/|V'|\geqslant \lambda\) 的解。这等同于找到让 \(|E'|-\lambda|V'|\geqslant 0\) 的解,也就是最大化 \(|E'|-\lambda|V'|\) 然后与 \(0\) 比较。
而 最大化 \(|E'|-\lambda|V'|\) 就是一道 0-1 线性规划 问题,一定比 0-1 分数规划要简单。对于特定的目标值 \(\lambda\),我们用 \(z(\lambda)\) 表示 \(|E'|-\lambda|V'|\) 能够达到的最大值。
令 \(\lambda_*\) 表示 \(|E'|/|V'|\) 能够达到的最大值,也就是我们的答案。此时我们有
\(z(\lambda)>0\iff \lambda<\lambda_*\)
\(z(\lambda)=0\iff \lambda=\lambda_*\)
\(z(\lambda)<0\iff \lambda>\lambda_*\)
请读者尝试自行证明这组不等式。实际上,这组不等式就是二分答案的可行性证明。
但是很明显我不是来聊二分答案的。
DinkelBach Algorithm
DinkelBach Algorithm 是一种解决分数规划的方法。类似于二分答案,它使用一个目标值 \(\lambda\);不同于二分答案,它不用二分。
Analogy: Newton's Method 牛顿迭代法
问题:不使用 sqrt(),如何找到 \(\sqrt 2\) 的近似值?
一种方法是二分,将二分值的平方与 \(2\) 比较,然后把可能值范围折半。
另一种远比二分法优秀的方法是 牛顿迭代法。首先,求 \(\sqrt 2\) 等同于找到多项式 \(P(x)=x^2-2\) 的正根。而牛顿迭代的具体做法是:
- 任取一个正数 \(x_0\)
- 找到点 \((x_0,P(x_0)=x_0^2-2)\) 并在此做 \(P(x)\) 的切线,其斜率为 \(P'(x_0)=2x_0\)
- 找到这条切线交于 \(x\) 轴的点 \((x_1,0)。\)
- 把 \(x_1\) 作为新的 \(x_0\),回到步骤 1 重新开始。用同样的方式得到 \(x_2,x_3,\cdots\)
这样你会获得一个序列 \((x_0,x_1,x_2,\cdots)\),其中 \(x_{n+1}=x_{n}-\frac{P(x_{n})}{P'(x_{n})}\)。 (中间的代数运算请读者自行尝试完成)
在图上看就是这个样子(设 \(x_0=2\)):红线表示 \(P(x)=x^2-2\),橙色虚线表示切线。
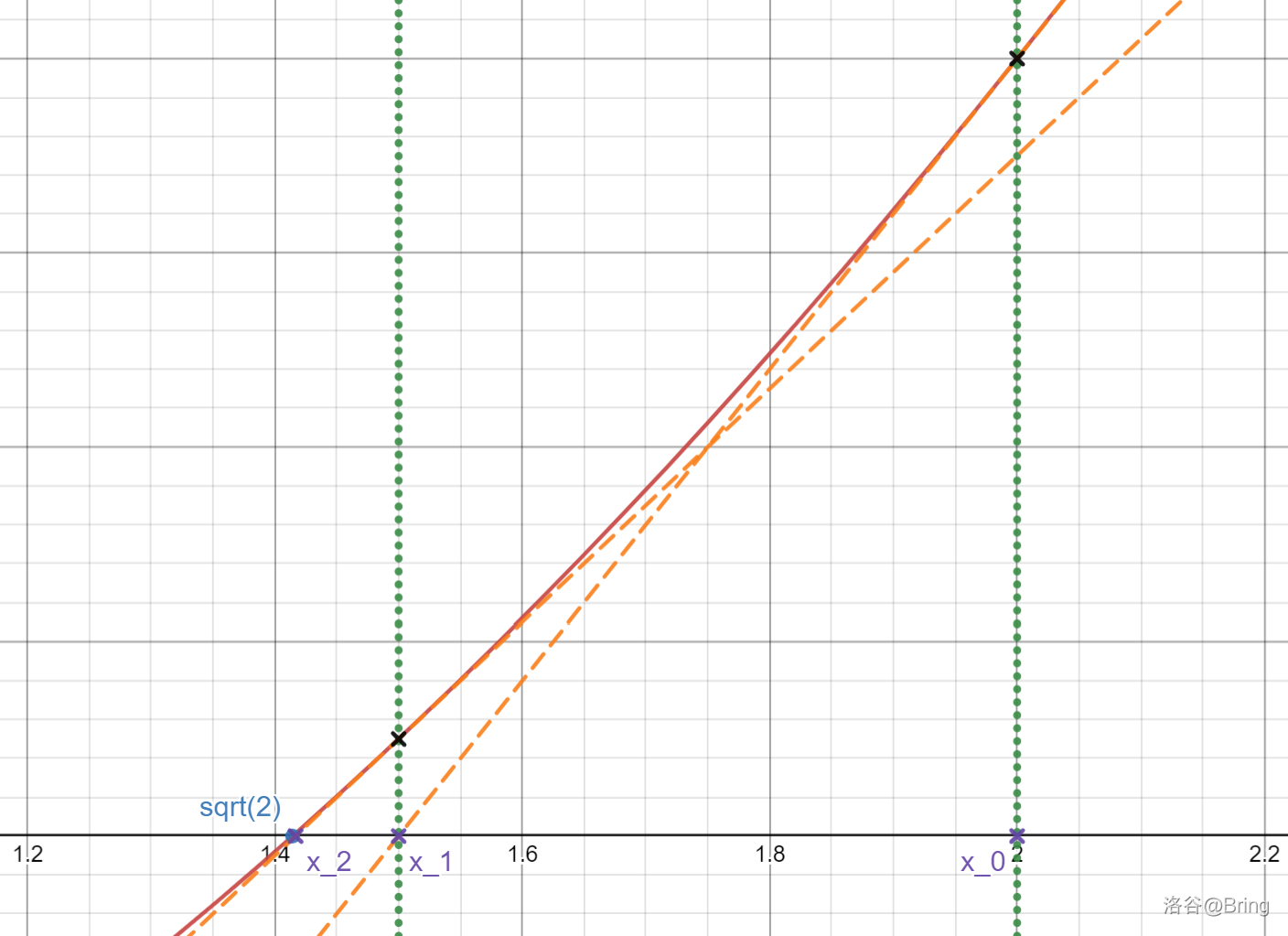
可以发现牛顿迭代法的收敛速度极快,远远超过了二分法。
Dinkelbach Algorithm 使用了类似的思想。
回到 Dinkelbach Algorithm
对于一个目标值 \(\lambda\),我们会进行最大化 \(|E'|-\lambda|V'|\) 的线性规划然后找到最大值 \(z(\lambda)\)。
但这次线性规划会给我们一个方案 \((V',E')\),而且它会有自己的值 \(\lambda'=|E'|/|V'|\)。Dinkelbach Algorithm 就是把 \(\lambda'\) 作为新的目标值 \(\lambda\),重复进行线性规划,直到某一时刻 \(z(\lambda)=0\),此时的 \(\lambda\) 就是要求的最大可能 \(|E'|/|V'|\)。
这个算法的正确性同样来自于前面的三个不等式。
我们先暂时停在这里,算法的具体实现和时间复杂度将会放在后面。现在我们来着手解决 0-1 线性规划问题:最大化 \(|E'|-\lambda|V'|\)。
找到 \(z(\lambda)\):最小割与有向图
重点在于如何表示 \(|E'|\)。相比于直接计算 \(V'\) 的矛盾对数,用 \(V'\) 内所有点的度数之和减去 \(V'\) 与 \(V\backslash V'\) 之间连的边数或许更加有用,因为从 \(V\) 里面选出子集 \(V'\) 时,\(V'\) 与 \(V\backslash V'\) 之间的边就会被去掉,这就像是割。
如果你也看过其它的题解,那么你应该是得到了一个类似于 \(|E'|=\frac{1}{2}(\sum_{u\in V'}d(u)-C[V',V\backslash V'])\) 的公式,其中 \(d(u)\) 表示点 \(u\) 的度数,而 \(C[V',V\backslash V']\) 表示从 \(V'\) 内和 \(V'\) 外的连接边数。然后就可以用最小割的方式来解决问题。
几乎所有的题解都将矛盾边 \((u,v)\) 当作 无向边 处理,具体操作就是在网络流建图时将正向边和反向边的容量都设为 \(1\)。这确实符合题意,因为题目中就是双向的矛盾。
但是其实我们也可以把 \((u,v)\) 当作 有向边 处理,也就是 \(u\) 单向地讨厌 \(v\)。
为什么?因为不管矛盾是单向还是双向的,都只有在双方均在场时才有矛盾。(不要去讨厌别人,否则别人也会讨厌你)
所以我们可以重新表示 \(|E'|\)。令 \(d(u)=|\{v\in V:(u\to v)\in E\}|\) 表示点 \(u\) 在 \(E\) 中的总 出度,并令 \(C[V',V\backslash V']=|\{(u\to v)\in E:u\in V',v\notin V'\}|\) 表示从 \(V'\) 里的点 向外连接 到 \(V'\) 外的点的边数,那么 \(|E'|=\sum_{u\in V'} d(u)-C[V',V\backslash V']\)。(省去一个 \(\frac{1}{2}\) 及其舒适)
于是 \(|E'|-\lambda|V'|=\sum_{u\in V'} (d(u)-\lambda)-C[V',V\backslash V']\)。既然都说了用最小割,那我们就式子反过来,变成 最小化 \(\lambda|V'|-|E'|=C[V',V\backslash V']+\sum_{u\in V'} (\lambda-d(u))\)。
这就是一道非常“最小割”的题目了。建立源点 \(s\) 和汇点 \(t\),我们把单向矛盾边 \(u\to v\) 的容量设为 \(1\),表示割掉它会使答案多 \(1\)。
对于每个点 \(u\),选定它会使答案多 \(\lambda-d(u)\)。因为这个值可能是负的,我们从 \(s\) 向 \(u\) 连容量为 \(m\) 的边,从 \(u\) 向 \(t\) 连 \(m+\lambda-d(u)\) 的边。这样做的目的是让边容量都为非负,所以 \(m\) 可以替换为任何一个靠谱的大数。这样做的正确性可以这么理解:在最小割中,这两条边会且只会切掉其中一个。这会让答案增加 \(nm\),是个常数,所以不影响。
于是,进行最大流最小割后,得到的流值就是 \(nm+\lambda|V'|-|E'|\) 的最小可能值,而在最小割中,属于 \(S\)(即仍然可以由 \(s\) 到达)的点就是被选出来的 \(V'\)。
可以这么理解:对于一个点 \(u\),如果 \((s\to u)\) 被割,那么 \(u\) 就属于 \(T(=\{t\}\cup V\backslash V')\),否则 \((u\to t)\) 必然被割且 \(u\) 属于 \(S\)。对于 \(u\in S,v\in T\),如果有矛盾边 \((u\to v)\in E\),则该边必然被割,否则存在增广路。
所以,最小割可以成功找到最优方案。
Implementation and Details
找到最小割的点集 \(S\)
一般的方法是从 \(s\) 开始搜索,走没有流完的边(不论正向还是反向),能够走到的点归于 \(S\),走不到的归于 \(T\)。这样的 \((S,T)\) 就是一个最小割。
如果你非常幸运地使用了 Dinic 算法,那么在算法结束返回最大流之前,就已经完成了一个对最终网络的 BFS。所以可以直接用 depth 数组来分划最小割:有 depth 的归于 \(S\),没有的归于 \(T\)。
Dinkelbach Algorithm 实现细节
现在,我们要把最小割嵌入 Dinkelbach Algorithm 来解决这一个 0-1 分数规划问题。步骤如下:
- 设置一个初始的目标值 \(\lambda\) (可以直接设 \(\lambda=0\))
- 用最小割找到 \(z(\lambda)\),即最大的 \(|E'|-\lambda|V'|\)(等同于找到最小的 \(\lambda|V'|-|E'|\))
- 将 \(|E'|/|V'|\) 设置为新的 \(\lambda\),从步骤 1 开始重复,直到\(z(\lambda)=0\)
但这不是最终的步骤。有一些细节需要处理:
- 在步骤 2 中,我们令 \(\mu=-z(\lambda)=\lambda|V'|-|E'|\),这个值等于最小割的流值减去 \(nm\)。经过代数变换,我们可以发现 \(|E'|/|V'|=\lambda-\mu/|V'|\)。所以我们只需要计算 \(|V'|\)(利用最小割)就可以直接知道 \(|E'|/|V'|\),也就是新一轮的目标值。(是不是感觉超级像牛顿迭代法的公式)
- 别忘了一点:我们要输出方案。当然,方案就是最小割里面的 \(S\) 部分。但是当我们在进行目标值为 \(\lambda_*\)(最大可能的 \(|E'|/|V'|\))的最小割时,流值为 \(nm\)。所以从 \(s\) 连向 \(V\) 中的点的所有边都会被割掉,也就是说我们拿到的最小割方案会是 \(V'=\empty\)。
这就像 \(0/0\) 可以是任何数。
为了防止出现这样的问题,在每个步骤 2 完成时,我们直接保存最小割方案。此时因为 \(\lambda\) 还未达到最大,流值 \(<nm\),所以一定存在没被割掉的 \(s\to u\)。这样我们就可以得到一个合法的方案。
而在某一时刻 \(\lambda=\lambda_*\) 达到最大时(判定方法为 \(z(\lambda)=0\),或流值 \(=nm\)),我们直接退出迭代并且把上一次的方案输出即可。
这是因为上一次的方案
- 是合法的;
- 它的\(|E'|/|V'|=\lambda=\lambda_*\) 是最大的。
所以这样我们就输出了最大化 \(|E'|/|V'|\) 的合法方案。
如果你读了二分答案的题解,你会发现他们在二分结束后用左边界值作为 \(\lambda\) 重新跑了一遍线性规划。这也是一样的想法,因为左边界只有在 \(\lambda<\lambda_*\) 时才更新,把自己的值改为 \(\lambda\),所以最后的左边界值一定不是最大 \(|E'|/|V'|\),但以它为目标值的线性规划会给出最大化 \(|E'|/|V'|\) 的方案。
Complexity Analysis
这里并不给出 Dinkelbach Algorithm 的时间复杂度证明,具体的证明可见
- Fractional Programming. II, on Dinkelbach's Algorithm
- An Analysis of Dinkelbach's Algorithm for 0-1 Fractional Programming Problems
论文证明了 Dinkelbach Algorithm 的答案收敛速度优于二分,在最坏情况下与二分相当。而且其实 Dinkelbach Algorithm 收敛速度也非常类似于 Newton's Method,因为两者都是求一个目标函数(前者为 \(z(\lambda)\),后者为 \(P(x)\))的零点,而两者都利用了函数的单调性和凸性。
所以,该算法的最坏时间复杂度是 \(O(n^2m\log nm)=O(n^2m\log n)\)(因为 \(m=O(n^2)\))。
空间复杂度为 \(O(n+m)=O(m)\)。
Code
以下为使用 Dinic 的代码实现。arr 表示最小割方案数组,ans 为文中的目标值 \(\lambda\),tmp 为流值,用 g[u] 表示从 \(u\) 出发的有向边数组。
注意特判 \(m=0\) 的情况 (非常良心的样例)。
//This program is written by Brian Peng.
#include<bits/stdc++.h>
using namespace std;
#define Rd(a) (a=rd())
#define Gc(a) (a=getchar())
#define Pc(a) putchar(a)
int rd(){
int x;char c(getchar());bool k;
while(!isdigit(c)&&c^'-')if(Gc(c)==EOF)exit(0);
c^'-'?(k=1,x=c&15):k=x=0;
while(isdigit(Gc(c)))x=x*10+(c&15);
return k?x:-x;
}
void wr(int a){
if(a<0)Pc('-'),a=-a;
if(a<=9)Pc(a|'0');
else wr(a/10),Pc((a%10)|'0');
}
signed const INF(0x3f3f3f3f),NINF(0xc3c3c3c3);
long long const LINF(0x3f3f3f3f3f3f3f3fLL),LNINF(0xc3c3c3c3c3c3c3c3LL);
#define Ps Pc(' ')
#define Pe Pc('\n')
#define Frn0(i,a,b) for(int i(a);i<(b);++i)
#define Frn1(i,a,b) for(int i(a);i<=(b);++i)
#define Frn_(i,a,b) for(int i(a);i>=(b);--i)
#define Mst(a,b) memset(a,b,sizeof(a))
#define File(a) freopen(a".in","r",stdin),freopen(a".out","w",stdout)
#define N (110)
#define Eps (1e-7)
int n,m,s,t,cr[N],d[N],u,v;
double ans,tmp;
struct E{int v;double w;int r;};
vector<E>e[N];
vector<int>g[N],arr;
void adde(int u,int v,double w);
bool bfs();
double dfs(int u,double a);
double mf();
signed main(){
while(1){
Rd(n),Rd(m);
if(!m){Pc('1'),Pe,Pc('1'),Pe;continue;}
t=n+1,ans=0;//源点标号 0,汇点 n+1
Frn1(i,1,n)g[i].clear();
Frn1(i,1,m)Rd(u),Rd(v),g[u].push_back(v);
while(1){
Frn1(i,0,t)e[i].clear();
Frn1(i,1,n)adde(s,i,m),adde(i,t,m+ans-g[i].size());
Frn1(i,1,n)for(int j:g[i])adde(i,j,1);
tmp=mf();
if(m*n-tmp<Eps)break;//找到答案时直接退出
arr.clear();//否则更新方案
Frn1(i,1,n)if(d[i])arr.push_back(i);
ans+=(m*n-tmp)/arr.size();
}
wr(arr.size()),Pe;//输出上一次的方案
for(int i:arr)wr(i),Pe;
Pe;
}
}
void adde(int u,int v,double w){
e[u].push_back({v,w,(int)(e[v].size())});
e[v].push_back({u,0,(int)(e[u].size())-1});
}
bool bfs(){
Mst(d,0);
queue<int>q({s});
d[s]=1;
while(!q.empty()){
int u(q.front());
q.pop();
for(E i:e[u])if(!d[i.v]&&i.w>Eps)d[i.v]=d[u]+1,q.push(i.v);
}
return d[t];
}
double dfs(int u,double a){
#define V e[u][i].v
#define W e[u][i].w
if(u==t||a<Eps)return a;
double tot(0),tmp;
for(int&i(cr[u]);i<e[u].size();++i)if(d[u]+1==d[V]){
tmp=dfs(V,min(a,W));
if(tmp>Eps){
W-=tmp,e[V][e[u][i].r].w+=tmp;
tot+=tmp,a-=tmp;
if(a<Eps)break;
}
}
return tot;
}
double mf(){
double f(0);
while(bfs())Mst(cr,0),f+=dfs(s,m*n);
return f;
}
Postscript
到此就是本篇题解的全部内容
感谢大家的阅读
新年快乐!あけましておめでとう!


