Solution: 题解 洛谷 P3380 【模板】二逼平衡树(树套树)的一种二逼写法(带修莫队+权值树状数组)
二逼平衡树的一种二逼写法
看到\(n,m\leqslant 5\times 10^4\)的数据范围,本蒟蒻不禁心生邪念
大家好,我非常喜欢暴力算法,所以用带修莫队过了这道题
前置芝士
1. 带修莫队
2. 树状数组
(本蒟蒻的博客还不够完善 sorry,之后会补上这些知识点)
正题
假设现在有这样一个神器可以高效满足以下操作:
-
加入一个数
-
删除一个数
-
求一个数的排名
-
求某排名的数
-
求一个数的前驱
-
求一个数的后继
诶,等等,这不就是普通平衡树吗???
别急,有更好的方法
现在假设我们有这个神器数据结构了,接下来就是带修莫队的事情了
带修莫队比普通莫队多了一个时间维,所以以\(b=n^{\frac{2}{3}}\)为长度对所有询问的\(l,r\)分块,具体来说就是对所有询问按照\(\lfloor l/b\rfloor,\lfloor r/b\rfloor\)和时间作三关键字排序
于是询问就变成了:
初始化指针\(l=1,r=0,t=0\),分别表示目前区间左端点,右端点和时间,并且初始化数据结构为空
设本次询问的指针为\(l_q,r_q,t_q\)
于是就要把\(l,r,t\)移动到\(l_q,r_q,t_q\),然后从数据结构中直接得到答案
具体移动方式如下:
设序列为\(a_{1..n}\),\(mt\)时间的操作位置为\(p_{t}\),改为数字\(k_{t}\)
如果\(l>l_q\),那么就将\(l-1\)加入数据结构,\(l=l-1\)
如果\(l<l_q\),那么就将\(l\)从数据结构中删除,\(l=l+1\)
\(r\)同理
如果\(t<t_q\),那么\(a_{p_{t+1}}\)就要改成\(k_{t+1}\),此时将\(a_{p_{t+1}}\)与\(k_{t+1}\)交换,如果\(a_{p_{t+1}}\)在\(l,r\)之间就要修改数据结构,最后\(t=t+1\)
如果\(t>t_q\),那么将\(a_{p_{t}}\)与\(k_t\)换回来,维护数据结构,\(t=t-1\)
在这种情况下,算法的时间复杂度已经有了\(O(n^\frac{5}{3})\)的因子
所以接下来就要看神器的表现了
解决这类问题,平衡树与线段树都具有\(O(\log n)\)的优秀复杂度,但是常数在这里吃不消
莫队已经是一种离线算法了
那我们就把离线的方法用到底吧!
Step 1: 离散化
将数据从\(10^8\)范围缩小到\(10^5\)范围,优化区间处理数据结构的复杂度
Step 2: 权值树状数组
线段树的常数还是太大,我们将树状数组扩展为权值树状数组
首先树状数组的两个基本方法:
-
\({\rm modify}\)\((x,v)\)表示将序列第\(x\)位值增加\(v\)
-
\({\rm query}\)\((x)\)表示求序列第\(x\)位前缀和
在此引入第三个方法\({\rm kth}(k)\)表示求最小的\(x\)使得\({\rm query}(x)\geqslant k\),也就是求第\(k\)名
从定义上看可以二分\(x\)完成,但是时间复杂度\(O(\log^2 n)\)
在此给出一个\(O(\log n)\)的方法:
设树状数组\(t_{1..m}\),我们需要进行一些扩展
定义\(rt\)为最大的一个\(\leqslant m\)的\(2\)的幂,为树状数组的根节点
于是\({\rm lowbit}(rt)\)是最大的
把树状数组想象成一棵二叉树,如图\(m=10,rt=8\),是不是很眼熟

如果\(u\)是奇数,那么它是叶子
定义\(u\)节点的左儿子\(ls\)为表示自己左半部分的节点,右儿子\(rs\)为\(ls\)加上\(u\)节点长度的的节点
好混乱,还是上图吧(红线表示左儿子,蓝线表示右儿子)
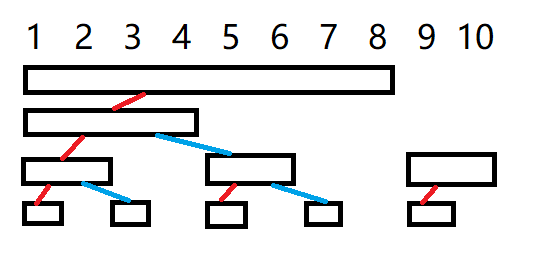
给出计算公式\(ls=u-{\rm lowbit}(u)/2,rs=u+{\rm lowbit}(u)/2\)
如果\(rs>m\),比如\(u=8\)的情况,就让它不断跳\(ls\)直到\(\leqslant m\)
现在开始实现\({\rm kth}(k)\)
初始化当前节点\(u=rt\),答案\(r=m\)
如果\(t_u\geqslant k\),说明\(u\)是一个可能答案,于是\(r=u,u=ls\)继续查找
如果\(t_u<k\),说明答案在\(u\)的右边,于是:
-
\(k=k-t_u\),因为\(t_{rs}\)不包含\(u\)及之前的内容,所以减去
-
\(u=rs\),并如果\(u>m\),重复执行\(u=ls\)直到\(u\leqslant m\)
最后,如果\(u\)是奇数,说明已经到达叶子,返回\(r\)为答案
P.s 在代码中为了方便直接设奇数\(u\)的\(ls=rs=0\)
于是这样就完成了\(O(\log n)\)的\({\rm kth}(k)\)方法
只要有了这些,就可以完成全部的查询
首先为了方便,在数据结构中直接加入一个\(2147483647\)和\(-2147483647\)
看一下需要的操作:
-
加入一个数\(x\):直接执行\({\rm modify}(x,1)\)
-
删除一个数\(x\):直接执行\({\rm modify}(x,-1)\)
-
求一个数\(x\)的排名:因为已经插入\(-2147483647\),所以\({\rm query}(x-1)\)就是答案
-
求排名为\(k\)的数:因为已经插入\(-2147483647\),所以答案是\({\rm kth}(k+1)\)
-
求一个数\(x\)的前驱:一个数的前驱是排名为\((x\)的排名\(-1)\)的数
-
求一个数的后继:一个数的后继是排名为\((\leqslant x\)的数的数量\(+1)\)的数
(没错,这个权值树状数组可以直接过掉可离线的普通平衡树模板,而且贼快)
最后是一些卡常技巧:
-
打开邪恶的Ofast:满数据开了\(10\)s,不开\(30\)s(哇塞)
-
事先将所有的\(a_i\)和\(k_i\)全部变成离散化之后的下标,这样才可以充分利用树状数组的优势:用了\(1\)s,不用\(10\)s(好可怕)
-
把脸洗干净
Time complexity: \(O(n^\frac{5}{3}\log n)\)(真惊险)
Memory complexity: \(O(n)\)
细节见代码(\(3.07\)s / \(3.19\)MB)(虽然时间可能有点长,但是空间绝对碾压树套树)
P.s 在这里离散化数组为\(d\),树状数组为\(t\),因为实在懒得开变量了就直接用\(*d\)(即\(d_0\))来储存长度,也就是文中的\(m\)
//This program is written by Brian Peng.
#pragma GCC optimize("Ofast","inline","no-stack-protector")
#include<bits/stdc++.h>
using namespace std;
#define Rd(a) (a=read())
#define Gc(a) (a=getchar())
#define Pc(a) putchar(a)
int read(){
int x;char c(getchar());bool k;
while(!isdigit(c)&&c^'-')if(Gc(c)==EOF)exit(0);
c^'-'?(k=1,x=c&15):k=x=0;
while(isdigit(Gc(c)))x=x*10+(c&15);
return k?x:-x;
}
void wr(int a){
if(a<0)Pc('-'),a=-a;
if(a<=9)Pc(a|'0');
else wr(a/10),Pc((a%10)|'0');
}
signed const INF(0x3f3f3f3f),NINF(0xc3c3c3c3);
long long const LINF(0x3f3f3f3f3f3f3f3fLL),LNINF(0xc3c3c3c3c3c3c3c3LL);
#define Ps Pc(' ')
#define Pe Pc('\n')
#define Frn0(i,a,b) for(int i(a);i<(b);++i)
#define Frn1(i,a,b) for(int i(a);i<=(b);++i)
#define Frn_(i,a,b) for(int i(a);i>=(b);--i)
#define Mst(a,b) memset(a,b,sizeof(a))
#define File(a) freopen(a".in","r",stdin),freopen(a".out","w",stdout)
#define N (50010)
#define D (100010)
#define Ls (u&1?0:u-((u&-u)>>1))
#define Rs (u&1?0:u|((u&-u)>>1))
int n,m,b,rt,t[D],d[D]{1,-2147483647},a[N],l(1),r,mt,ans[N];
struct Q{int o,l,r,k,t,i;}q[N];
struct{int p,k;}o3[N];
bool cmp(int a,int b,bool c){return a!=b?a<b:c;}
void mdf(int x,int v){while(x<=*d)t[x]+=v,x+=x&-x;}
int ps(int x){return lower_bound(d+1,d+*d+1,x)-d;}
int qry(int x){int r(0);while(x)r+=t[x],x^=x&-x;return r;}
int kth(int x);
signed main(){
Rd(n),Rd(m),b=pow(n,0.67)+1;
Frn1(i,1,n)d[++*d]=Rd(a[i]);
Frn1(i,1,m)if(Rd(q[i].o)==3)o3[++mt]={read(),Rd(d[++*d])},--i,--m;
else q[i]={q[i].o,read(),read(),read(),mt,i},q[i].o==2?0:(d[++*d]=q[i].k);
d[++*d]=2147483647,sort(d+2,d+*d),rt=*d=unique(d+1,d+*d+1)-d-1;
Frn1(i,1,n)a[i]=ps(a[i]);
Frn1(i,1,mt)o3[i].k=ps(o3[i].k);
while(rt^(rt&-rt))rt^=rt&-rt;
sort(q+1,q+m+1,[](Q x,Q y){return cmp(x.l/b,y.l/b,cmp(x.r/b,y.r/b,x.t<y.t));});
mdf(1,1),mdf(*d,1),mt=0;
Frn1(i,1,m){
while(r<q[i].r)mdf(a[++r],1);
while(l>q[i].l)mdf(a[--l],1);
while(r>q[i].r)mdf(a[r--],-1);
while(l<q[i].l)mdf(a[l++],-1);
while(mt<q[i].t){
++mt,swap(a[o3[mt].p],o3[mt].k);
if(l<=o3[mt].p&&o3[mt].p<=r)mdf(o3[mt].k,-1),mdf(a[o3[mt].p],1);
}
while(mt>q[i].t){
if(l<=o3[mt].p&&o3[mt].p<=r)mdf(a[o3[mt].p],-1),mdf(o3[mt].k,1);
swap(a[o3[mt].p],o3[mt].k),--mt;
}
switch(q[i].o){
case 1:ans[q[i].i]=qry(ps(q[i].k)-1);break;
case 2:ans[q[i].i]=d[kth(q[i].k+1)];break;
case 4:ans[q[i].i]=d[kth(qry(ps(q[i].k)-1))];break;
case 5:ans[q[i].i]=d[kth(qry(ps(q[i].k))+1)];
}
}
Frn1(i,1,m)wr(ans[i]),Pe;
exit(0);
}
int kth(int k){
int u(rt),r(*d);
while(u)if(k<=t[u])r=u,u=Ls;
else{k-=t[u],u=Rs;while(u>*d)u=Ls;}
return r;
}


