[POJ2286]The Rotation Game

Description

The rotation game uses a # shaped board, which can hold 24 pieces of square blocks (see Fig.1). The blocks are marked with symbols 1, 2 and 3, with exactly 8 pieces of each kind.

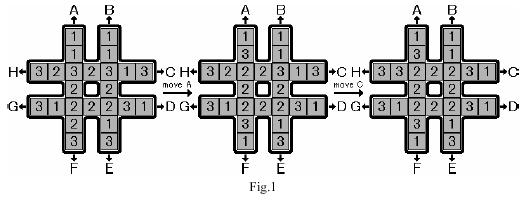
Initially, the blocks are placed on the board randomly. Your task is to move the blocks so that the eight blocks placed in the center square have the same symbol marked. There is only one type of valid move, which is to rotate one of the four lines, each consisting of seven blocks. That is, six blocks in the line are moved towards the head by one block and the head block is moved to the end of the line. The eight possible moves are marked with capital letters A to H. Figure 1 illustrates two consecutive moves, move A and move C from some initial configuration.

Input

The input consists of no more than 30 test cases. Each test case has only one line that contains 24 numbers, which are the symbols of the blocks in the initial configuration. The rows of blocks are listed from top to bottom. For each row the blocks are listed from left to right. The numbers are separated by spaces. For example, the first test case in the sample input corresponds to the initial configuration in Fig.1. There are no blank lines between cases. There is a line containing a single `0' after the last test case that ends the input.

Output

For each test case, you must output two lines. The first line contains all the moves needed to reach the final configuration. Each move is a letter, ranging from `A' to `H', and there should not be any spaces between the letters in the line. If no moves are needed, output `No moves needed' instead. In the second line, you must output the symbol of the blocks in the center square after these moves. If there are several possible solutions, you must output the one that uses the least number of moves. If there is still more than one possible solution, you must output the solution that is smallest in dictionary order for the letters of the moves. There is no need to output blank lines between cases.

Sample Input

1 1 1 1 3 2 3 2 3 1 3 2 2 3 1 2 2 2 3 1 2 1 3 3
1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3
0

Sample Output

AC
2
DDHH
2

---

日常吐槽：调了半天玄学错误，最后发现我递归的时候修改了全局变量的值...这个错误调了我大概一个小时...
哎还是太菜了，要加油啊。
然后过了样例提交，WA，改了改某些自己认为不太对的地方，WA，看了讨论，发现没有在不用移动的情况下输出第二行，改了，WA，重看，发现没删调试语句。
AC！！！！！547Ms感觉不错。
这题用了我大概两个小时。
算法：搜索。
搜索框架：dfs(显然)。
但是这样是显然不能过的。
剪枝思路：因为可能的步数不是很多，所以可以考虑迭代加深A*，下面的问题是我们如何确定估价函数。
观察到题目特点，每次操作最多只能增加中间的一个数字，如果中间的格子数字最多出现次数是cnt，那么至少移动8-cnt步才能到达，可以想象这个估价函数非常强(雾)。
然后献上自己丑陋的代码。
也纪念一下我的第一道IDA*的题目。

---

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
#define reg register
inline int read() {
    int res=0;char ch=getchar();bool fu=0;
    while(!isdigit(ch))fu|=(ch=='-'), ch=getchar();
    while(isdigit(ch))res=(res<<3)+(res<<1)+(ch^48),ch=getchar();
    return fu?-res:res;
}
int a[8][8];
int ans, road[105];
bool Flag;
int mark;

void IDAstar(int x[8][8], int dep) {
//    printf("%d::\n", dep);
//    for (int i=1;i<=7;i++,puts("")) for(int j=1;j<=7;j++) if(!a[i][j]) printf("  ");else printf("%d ",x[i][j]);puts("");
    int b[8][8];
    if (Flag) return;
    int mx = 1;
    int cnt[4] = {0};
    for (reg int i = 3 ; i <= 5 ; i ++) for (reg int j = 3 ; j <= 5 ; j ++) cnt[x[i][j]]++;
    for (reg int i = 2 ; i <= 3 ; i ++) if (cnt[i] > cnt[mx]) mx = i;
    if (dep == ans) {
        if (cnt[mx] == 8) {
            Flag = 1, mark = mx;
            for (reg int i = 0 ; i < dep ; i ++) printf("%c", road[i] + 'A' - 1);
            printf("\n%d\n", mx);
        }
//        for (int i=1;i<=3;i++) printf("%d ", cnt[i]);puts("");
        return ;
    }
    if (dep + 8 - cnt[mx] > ans) return;
    
    // A:
    memcpy(b, x, sizeof b);
    for (reg int i = 1 ; i < 7 ; i ++) b[i][3] = x[i + 1][3];
    b[7][3] = x[1][3];
    road[dep] = 1;
    IDAstar(b, dep + 1);
    // B:
    memcpy(b, x, sizeof b);
    for (reg int i = 1 ; i < 7 ; i ++) b[i][5] = x[i + 1][5];
    b[7][5] = x[1][5];
    road[dep] = 2;
    IDAstar(b, dep + 1);
    // C:
    memcpy(b, x, sizeof b);
    for (reg int i = 7 ; i > 1 ; i --) b[3][i] = x[3][i - 1];
    b[3][1] = x[3][7];
    road[dep] = 3;
    IDAstar(b, dep + 1);
    
    // D:
    memcpy(b, x, sizeof b);
    for (reg int i = 7 ; i > 1 ; i --) b[5][i] = x[5][i - 1];
    b[5][1] = x[5][7];
    road[dep] = 4;
    IDAstar(b, dep + 1);
    // E:
    memcpy(b, x, sizeof b);
    for (reg int i = 7 ; i > 1 ; i --) b[i][5] = x[i - 1][5];
    b[1][5] = x[7][5];
    road[dep] = 5;
    IDAstar(b, dep + 1);
    // F:
    memcpy(b, x, sizeof b);
    for (reg int i = 7 ; i > 1 ; i --) b[i][3] = x[i - 1][3];
    b[1][3] = x[7][3];
    road[dep] = 6;
    IDAstar(b, dep + 1);    
    // G:
    memcpy(b, x, sizeof b);
    for (reg int i = 1 ; i < 7 ; i ++) b[5][i] = x[5][i + 1];
    b[5][7] = x[5][1];
    road[dep] = 7;
    IDAstar(b, dep + 1);
    // H:
    memcpy(b, x, sizeof b);
    for (reg int i = 1 ; i < 7 ; i ++) b[3][i] = x[3][i + 1];
    b[3][7] = x[3][1];
    road[dep] = 8;
    IDAstar(b, dep + 1);
}

int main()
{
    while(1) 
    {
        a[1][3] = read();if (!a[1][3]) return 0;
        a[1][5] = read();
        a[2][3] = read(), a[2][5] = read();
        for (reg int i = 1 ; i <= 7 ; i ++) a[3][i] = read();
        a[4][3] = read(), a[4][5] = read();
        for (reg int i = 1 ; i <= 7 ; i ++) a[5][i] = read();
        a[6][3] = read(), a[6][5] = read();
        a[7][3] = read(), a[7][5] = read();
//        for (int i=1;i<=7;i++,puts("")) for(int j=1;j<=7;j++) if(!a[i][j]) printf("  ");else printf("%d ",a[i][j]);
        int mx = 1;
        int cnt[4] = {0};
        for (reg int i = 3 ; i <= 5 ; i ++) for (reg int j = 3 ; j <= 5 ; j ++) cnt[a[i][j]]++;
        for (reg int i = 2 ; i <= 3 ; i ++) if (cnt[i] > cnt[mx]) mx = i;
        if (cnt[mx] == 8) {printf("No moves needed\n");printf("%d\n", mx);continue;}
        
        ans = 1;
        Flag = 0;
        for ( ; !Flag ; IDAstar(a, 0), ans ++);
        
//        for (reg int i = 1 ; i <= ans ; i ++) printf("%d", road[i]);
//        puts("");printf("%d\n", mark);
    }
    return 0;
}