[Noip2017] 列队
题目描述
Sylvia 是一个热爱学习的女♂孩子。
前段时间,Sylvia 参加了学校的军训。众所周知,军训的时候需要站方阵。
Sylvia 所在的方阵中有n×mn \times mn×m名学生,方阵的行数为 nnn,列数为 mmm。
为了便于管理,教官在训练开始时,按照从前到后,从左到右的顺序给方阵中 的学生从 1 到 n×mn \times mn×m 编上了号码(参见后面的样例)。即:初始时,第 iii 行第 jjj 列 的学生的编号是(i−1)×m+j(i-1)\times m + j(i−1)×m+j。
然而在练习方阵的时候,经常会有学生因为各种各样的事情需要离队。在一天 中,一共发生了 qq q件这样的离队事件。每一次离队事件可以用数对(x,y)(1≤x≤n,1≤y≤m)(x,y) (1 \le x \le n, 1 \le y \le m)(x,y)(1≤x≤n,1≤y≤m)描述,表示第 xxx 行第 yyy 列的学生离队。
在有学生离队后,队伍中出现了一个空位。为了队伍的整齐,教官会依次下达 这样的两条指令:
-
向左看齐。这时第一列保持不动,所有学生向左填补空缺。不难发现在这条 指令之后,空位在第 xxx 行第 mmm 列。
-
向前看齐。这时第一行保持不动,所有学生向前填补空缺。不难发现在这条 指令之后,空位在第 nnn 行第 mmm 列。
教官规定不能有两个或更多学生同时离队。即在前一个离队的学生归队之后, 下一个学生才能离队。因此在每一个离队的学生要归队时,队伍中有且仅有第 nnn 行 第 mmm 列一个空位,这时这个学生会自然地填补到这个位置。
因为站方阵真的很无聊,所以 Sylvia 想要计算每一次离队事件中,离队的同学 的编号是多少。
注意:每一个同学的编号不会随着离队事件的发生而改变,在发生离队事件后 方阵中同学的编号可能是乱序的。
输入输出格式
输入格式:输入共 q+1q+1q+1 行。
第 1 行包含 3 个用空格分隔的正整数 n,m,qn, m, qn,m,q,表示方阵大小是 nnn 行 mmm 列,一共发 生了 qqq 次事件。
接下来 qqq 行按照事件发生顺序描述了 qqq 件事件。每一行是两个整数 x,yx, yx,y,用一个空 格分隔,表示这个离队事件中离队的学生当时排在第 xxx 行第 yyy 列。
输出格式:按照事件输入的顺序,每一个事件输出一行一个整数,表示这个离队事件中离队学 生的编号。
输入输出样例
说明
【输入输出样例 1 说明】
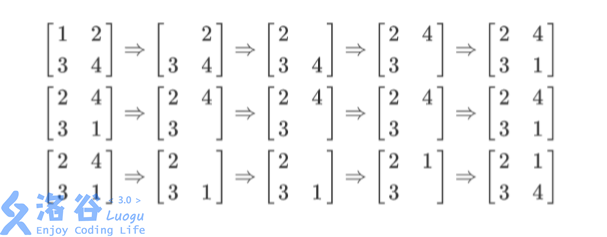
列队的过程如上图所示,每一行描述了一个事件。 在第一个事件中,编号为1 11 的同学离队,这时空位在第一行第一列。接着所有同学 向左标齐,这时编号为 22 2的同学向左移动一步,空位移动到第一行第二列。然后所有同 学向上标齐,这时编号为4 4 4的同学向上一步,这时空位移动到第二行第二列。最后编号 为1 11 的同学返回填补到空位中。
【数据规模与约定】
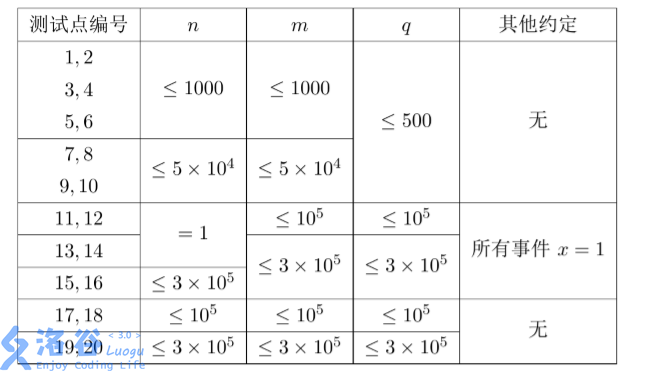
数据保证每一个事件满足 1≤x≤n,1≤y≤m1 \le x \le n,1 \le y \le m1≤x≤n,1≤y≤m
用fhq_treap维护。
维护每一行的前m-1个元素和第m列的元素。
没次询问$\large (x, y)$,如果y等于m,就在第m列的treap里把第x个位置的元素放到最后。
否则把第m列的第x个元素放在x行的最后一个, 将x行的第y个元素放在第m列的最后一个。
然后不能维护点,空间开不下,所以维护一个区间(第一次见)。
#include <iostream> #include <cstdio> #include <cstring> #include <ctime> #include <cstdlib> using namespace std; #define int long long inline int read() { int res=0;char ch=getchar(); while(!isdigit(ch))ch=getchar(); while(isdigit(ch))res=(res<<3)+(res<<1)+(ch^48), ch=getchar(); return res; } #define reg register #define N 300005 int n, m, q; int cnt; int root[N]; namespace fhq { int L[N*10], R[N*10], pri[N*10], ch[N*10][2], siz[N*10]; inline int newnode(int l, int r) { cnt++; L[cnt] = l, R[cnt] = r; pri[cnt] = rand(); siz[cnt] = r - l + 1; return cnt; } inline void update (int o) { siz[o] = siz[ch[o][0]] + siz[ch[o][1]] + R[o] - L[o] + 1; } inline int Merge(int x, int y) { if (x * y == 0) return x + y; if (pri[x] < pri[y]) { ch[x][1] = Merge(ch[x][1], y); update(x); return x; } else { ch[y][0] = Merge(x, ch[y][0]); update(y); return y; } } inline void make(int o, int k) { if (R[o] - L[o] + 1 <= k) return ; int rr = L[o] + k - 1; int newn = newnode(rr + 1, R[o]); R[o] = rr; ch[o][1] = Merge(newn, ch[o][1]); update(o); } inline void Split(int o, int k, int &x, int &y) //×ó×óê÷′óD??ak { if (!o) {x = 0, y = 0;return ;} if (siz[ch[o][0]] >= k) y = o, Split(ch[o][0], k, x, ch[o][0]); else { if (k - siz[ch[o][0]] < R[o] - L[o] + 1) make(o, k - siz[ch[o][0]]); x = o; Split(ch[o][1], k - siz[ch[o][0]] - (R[o] - L[o] + 1), ch[o][1], y); } update(o); } }using namespace fhq; signed main() { n = read(), m = read(), q = read(); srand((unsigned)(time(NULL))); for (reg int i = 1 ; i <= n ; i ++) root[i] = newnode((i - 1) * m + 1, (i - 1) * m + m - 1); for (reg int i = 1 ; i <= n ; i ++) root[n+1] = Merge(root[n+1], newnode(i * m, i * m)); while(q--) { int x = read(), y = read(); if (y == m) { int a, b, c, d, e; Split(root[n+1], x - 1, a, b); Split(b, 1, c, d); printf("%lld\n", L[c]); e = Merge(a, d); root[n+1] = Merge(e, c); } else { int a, b, c, d, e, f, g, h, i, j; Split(root[x], y - 1, a, b); Split(b, 1, c, d); printf("%lld\n", L[c]); e = Merge(a, d); Split(root[n+1], x - 1, f, g); Split(g, 1, h, i); j = Merge(f, i); root[x] = Merge(e, h); root[n+1] = Merge(j, c); } } return 0; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号