[Noip1997] 棋盘问题（2）

题目描述

在N×NN \times NN×N的棋盘上(1≤N≤10)(1≤N≤10)(1≤N≤10)，填入1,2,…,N21,2,…,N^21,2,…,N2共N2N^2N2个数，使得任意两个相邻的数之和为素数。

例如：当N=2N=2N=2时，有：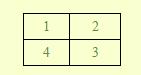

其相邻数的和为素数的有：

1+2,1+4,4+3,2+31+2,1+4,4+3,2+31+2,1+4,4+3,2+3

当N=4N=4N=4时，一种可以填写的方案如下：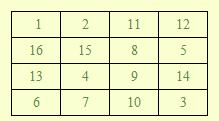

在这里我们约定：左上角的格子里必须填数字111。

输入输出格式

输入格式：

一个数NNN

输出格式：

如有多种解，则输出第一行、第一列之和为最小的排列方案；若无解，则输出“NO”。

输入输出样例

输入样例#1： 复制

1

输出样例#1： 复制

NO

输入样例#2： 复制

2

输出样例#2： 复制

1 2

---

一开始没看到第一行和第一列的和最小，一直以为只用第一列的和最小...
其实都差不多...
就是正常的搜索， 加上一维判断是不是第一列第一行搜完了。
我采取的策略是先搜第一行第一列，然后从(2, 2)点开始搜索。

---

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
using namespace std;
#define reg register
inline int read() {
    int res=0;char ch=getchar();
    while(!isdigit(ch)) ch=getchar();
    while(isdigit(ch))res=(res<<3)+(res<<1)+(ch^48),ch=getchar();
    return res;
}

int n;
bool is[105*2];
int use[105];
int a[15][15];

inline void dfs(int x, int y, int end, int beg)
{
    //printf("%d %d\n", x, y);
    if (end) {
        for (reg int i = 1 ; i <= n ; i ++, puts(""))
            for (reg int j = 1 ; j <= n ; j ++)
                printf("%d ", a[i][j]);
        exit(0);
    }
    bool flag = 0;
    for (reg int i = 2 ; i <= n * n ; i ++)
    {
        if (use[i]) continue;
        if ((x == 1 or is[i+a[x-1][y]]) and (y == 1 or is[i+a[x][y-1]]))
        {
            int x1 = x, y1 = y + 1;
            if (beg) {
                if (x == 1 and y >= 2) x1 = 1, y1 = y + 1;
                if (y == 1 and x >= 2) x1 = x + 1, y1 = 1;
                if (x == 1 and y == n) x1 = 2, y1 = 1;
            }
            flag = 1;
            int tmp = 0, tmp2 = beg;
            if (x == n and y == n) tmp = 1;
            if (x == n and y == 1) tmp2 = 0, x1 = 2, y1 = 2;
            if (!beg and y == n and x != n) x1 = x + 1, y1 = 2;
            a[x][y] = i;
            use[i] = 1;
            dfs(x1, y1, tmp, tmp2);
            use[i] = 0;
            a[x][y] = 0;
        }
    }
    if (!flag) return ;
}

int main()
{
    n = read();
    if (n == 1) return puts("NO"), 0;
    for (reg int i = 2 ; i <= n * n * 2 ; i ++)
    {
        for (reg int j = 2 ; j * j <= i ; j ++)
            if (i % j == 0) {is[i] = 0;goto End;}
        is[i] = 1;
        End:;
    }
    a[1][1] = 1;
    use[1] = 1;
    dfs(1, 2, 0, 1);
    puts("NO");
    return 0;
}