[Noip 2015] 斗地主
题目描述
牛牛最近迷上了一种叫斗地主的扑克游戏。斗地主是一种使用黑桃、红心、梅花、方片的AAA到KKK加上大小王的共545454张牌来进行的扑克牌游戏。在斗地主中,牌的大小关 系根据牌的数码表示如下:3<4<5<6<7<8<9<10<J<Q<K<A<2<小王<大王3<4<5<6<7<8<9<10<J<Q<K<A<2<\text{小王}<\text{大王}3<4<5<6<7<8<9<10<J<Q<K<A<2<小王<大王,而花色并不对牌的大小产生影响。每一局游戏中,一副手牌由 nnn 张牌组成。游戏者每次可以根据规定的牌型进行出牌,首先打光自己的手牌一方取得游戏的胜利。
现在,牛牛只想知道,对于自己的若干组手牌,分别最少需要多少次出牌可以将它们打光。请你帮他解决这个问题。
需要注意的是,本题中游戏者每次可以出手的牌型与一般的斗地主相似而略有不同。具体规则如下:
本题数据随机,不支持hack,要hack或强力数据请点击这里
输入输出格式
输入格式:第一行包含用空格隔开的2个正整数 T,nT,nT,n ,表示手牌的组数以及每组手牌的张数。
接下来 TTT 组数据,每组数据 nnn 行,每行一个非负整数对 ai,bia_i,b_iai,bi ,表示一张牌,其中 aia_iai 表示牌的数码, bib_ibi 表示牌的花色,中间用空格隔开。特别的,我们用 111 来表示数码 AAA, 111111 表示数码J JJ, 121212 表示数码Q QQ, 131313 表示数码 KKK;黑桃、红心、梅花、方片分别用 1−41-41−4 来表示;小王的表示方法为 010101 ,大王的表示方法为 020202 。
输出格式:共 TTT 行,每行一个整数,表示打光第 iii 组手牌的最少次数。
输入输出样例
1 17 12 3 4 3 2 3 5 4 10 2 3 3 12 2 0 1 1 3 10 1 6 2 12 1 11 3 5 2 12 4 2 2 7 2
6
说明
样例1说明
共有111组手牌,包含8张牌:方片777,方片888,黑桃999,方片101010,黑桃JJJ,黑桃555,方片AAA以及黑桃AAA。可以通过打单顺子(方片777,方片888,黑桃999,方片101010,黑桃JJJ),单张牌(黑桃555)以及对子牌(黑桃AAA以及方片AAA)在333次内打光。
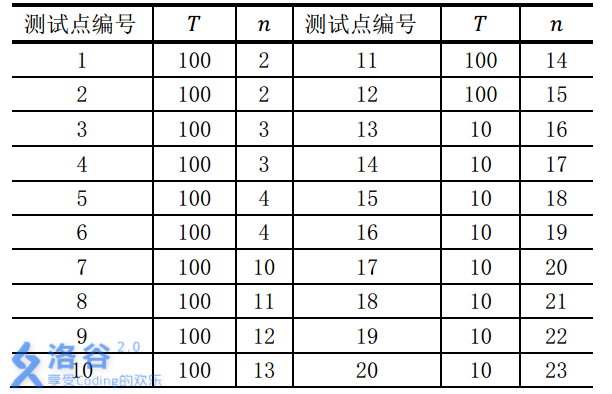
对于不同的测试点, 我们约定手牌组数TTT与张数nnn的规模如下:
数据保证:所有的手牌都是随机生成的。
这道题真的让我感觉我的能力距noip还差远了。
哒哒哒哒哒暴搜都不会写。
说实话这题我看了题解,要不贪心的策略都想不出来。
代码能力太差,写多了就调不出来。
先爆搜顺子,根据题解的意思, 三顺子其实没必要出, 因为不如让他三带1或2,那样更优。
然后贪心爆搜,四带二, 四带两对, 四张炸, 三带一,三带一对, 三个单出,每一个情况都搜索一遍。
剩下的一定就是单和对子了。
再加上最优化剪枝过了。
一开始回溯的时候用的栈存所有改变过的,然后再退栈。
不知为何萎了。
于是又参考了题解233.
#include <iostream> #include <cstdio> #include <cstdlib> #include <algorithm> #include <cstring> using namespace std; inline int read() { int res = 0;char ch=getchar(); while(!isdigit(ch)) ch=getchar(); while(isdigit(ch)) res=(res<<3)+(res<<1)+(ch^48), ch=getchar(); return res; } #define reg register int T, n; int hav[17];//how many cards at beginning, 14 means the king int ans; inline bool sanshun(int i) { if (hav[i] >= 3 and hav[i%13+1] >= 3) return 1; return 0; } inline bool shuangshun(int i) { if (hav[i] >= 2 and hav[i+1] >= 2 and hav[(i+1)%13+1] >= 2) return 1; return 0; } inline bool danshun(int i) { if (hav[i] >= 1 and hav[i+1] >= 1 and hav[i+2] >= 1 and hav[i+3] >= 1 and hav[(i+3)%13+1] >= 1) return 1; return 0; } inline int four() { for (reg int i = 1 ; i <= 14 ; i ++) if (hav[i] >= 4) return i; return -1; } inline int three() { for (reg int i = 1 ; i <= 14 ; i ++) if (hav[i] >= 3) return i; return -1; } void dfs(int dep, int lef) { if (dep >= ans) return; if (!lef) {ans = dep;return ;} for (reg int i = 3 ; i <= 12 ; i ++) { //双顺子 if (shuangshun(i)) { int k = i; while(hav[k] >= 2 and k != 2) { hav[k] -= 2; if (k - i + 1 >= 3) dfs(dep + 1, lef - (k - i + 1)); k++; if (k == 14) k = 1; } if (k == 1) k = 14; // 13 -> 1 else if (k == 2) k = 15; // 1 -> 2 dfs(dep + 1, lef - (k - i)); if (k == 15) k--, hav[1] += 2; for (reg int j = i ; j <= k - 1 ; j ++) hav[j] += 2; } } for (reg int i = 3 ; i <= 10 ; i ++) { //单顺子 if (danshun(i)) { int k = i; while(hav[k] >= 1 and k != 2) { hav[k]--; if (k - i + 1 >= 5) dfs(dep + 1, lef - (k - i + 1)); k++; if (k == 14) k = 1; } if (k == 1) k = 14; else if (k == 2) k = 15; dfs(dep + 1, lef - (k - i)); if (k == 15) k--, hav[1] ++; for (reg int j = i ; j <= k - 1 ; j ++) hav[j] ++; } } //四带~~~ int k = four(); if (k != -1) { hav[k] -= 4; for (reg int i = 1 ; i <= 14 ; i ++) { if (!hav[i]) continue; for (reg int j = 1 ; j <= 14 ; j ++) { if (i == j or !hav[j]) continue; if (hav[i] >= 2 and hav[j] >= 2) //四带两对 { hav[i] -= 2, hav[j] -= 2; dfs(dep + 1, lef - 8); hav[i] += 2, hav[j] += 2; } if (hav[i] and hav[j]) //四带两张 { hav[i]--, hav[j]--; dfs(dep + 1, lef - 6); hav[i]++, hav[j]++; } } } dfs(dep + 1, lef - 4);//comboon! hav[k] += 4; } //三带~~~ k = three(); if (k != -1) { hav[k] -= 3; for (reg int i = 1 ; i <= 14 ; i ++) { if (hav[i] >= 2) { hav[i] -= 2; dfs(dep + 1, lef - 5); hav[i] += 2; } if (hav[i]) { hav[i]--; dfs(dep + 1, lef - 4); hav[i]++; } } dfs(dep + 1, lef - 3);//单三 hav[k] += 3; } //现在只剩下对和单了 int sum = 0; for (reg int i = 1 ; i <= 14 ; i ++) if (hav[i]) sum ++; dfs(dep + sum, 0); } int main() { T = read(), n = read(); while(T--) { memset(hav, 0, sizeof hav); for (reg int i = 1 ; i <= n ; i ++) { int x = read(), y = read(); if (x != 0) hav[x]++; else hav[14]++; } ans = 14; dfs(0, n); printf("%d\n", ans); } return 0; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号