NOIP2015 运输计划
题目背景
公元 204420442044 年,人类进入了宇宙纪元。
题目描述
公元 204420442044 年,人类进入了宇宙纪元。
L 国有 $nnn$ 个星球,还有 $n−1n-1n−1$ 条双向航道,每条航道建立在两个星球之间,这 $n−1n-1n−1$ 条航道连通了 $LLL$ 国的所有星球。
小 P 掌管一家物流公司, 该公司有很多个运输计划,每个运输计划形如:有一艘物流飞船需要从 $uiu_iui$ 号星球沿最快的宇航路径飞行到 $viv_ivi$ 号星球去。显然,飞船驶过一条航道是需要时间的,对于航道 jjj ,任意飞船驶过它所花费的时间为 $tjt_jtj$ ,并且任意两艘飞船之间不会产生任何干扰。
为了鼓励科技创新,$ LLL$ 国国王同意小$ PPP$ 的物流公司参与$ LLL$ 国的航道建设,即允许小 $PPP$ 把某一条航道改造成虫洞,飞船驶过虫洞不消耗时间。
在虫洞的建设完成前小 P 的物流公司就预接了$ mmm$ 个运输计划。在虫洞建设完成后,这 $mmm$ 个运输计划会同时开始,所有飞船一起出发。当这 $mmm$ 个运输计划都完成时,小$ PPP$ 的物流公司的阶段性工作就完成了。
如果小 $PPP $可以自由选择将哪一条航道改造成虫洞, 试求出小 $PPP$ 的物流公司完成阶段性工作所需要的最短时间是多少?
输入输出格式
输入格式:第一行包括两个正整数 n,mn, mn,m ,表示 L 国中星球的数量及小 P 公司预接的运输计划的数量,星球从 111 到 nnn 编号。
接下来 n−1n-1n−1 行描述航道的建设情况,其中第 iii 行包含三个整数 ai,bia_i, b_iai,bi 和 tit_iti ,表示第 iii 条双向航道修建在 aia_iai 与 bib_ibi 两个星球之间,任意飞船驶过它所花费的时间为 tit_iti 。数据保证 1≤ai,bi≤n1 \leq a_i,b_i \leq n1≤ai,bi≤n 且 0≤ti≤10000 \leq t_i \leq 10000≤ti≤1000 。
接下来 mmm 行描述运输计划的情况,其中第 jjj 行包含两个正整数 uju_juj 和 vjv_jvj ,表示第 jjj 个运输计划是从 uju_juj 号星球飞往 vjv_jvj 号星球。数据保证 1≤ui,vi≤n1 \leq u_i,v_i \leq n1≤ui,vi≤n
输出格式:一个整数,表示小 PPP 的物流公司完成阶段性工作所需要的最短时间。
输入输出样例
6 3 1 2 3 1 6 4 3 1 7 4 3 6 3 5 5 3 6 2 5 4 5
11
说明
所有测试数据的范围和特点如下表所示
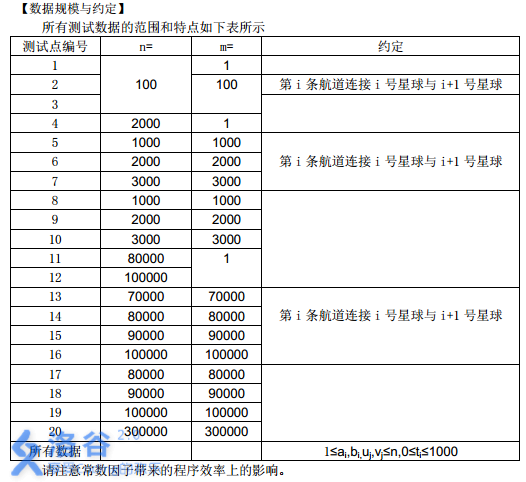
请注意常数因子带来的程序效率上的影响。
sb了这题做了一个半小时。
一个sb问题气死了。
二分答案,把大于mid的路径的所有边都加1,用树上差分来完成。
然后找有没有一条边被覆盖恰好大于mid的路径的条数次,然后判断是否减去后可以达到mid。
然后就完了,一点都不难,我就是个sb。
#include <iostream> #include <cstdio> #include <cstdlib> #include <cstring> #include <queue> using namespace std; inline int read(){ #define gc getchar() int res=0;char ch=gc; while(!isdigit(ch))ch=gc; while(isdigit(ch)){res=(res<<3)+(res<<1)+(ch^48);ch=gc;} return res; } int n, m, ans = 1e9; bool ffl = 0; struct edge{ int nxt, to, val; }ed[600005]; int head[300005], cnt; inline void add(int x, int y , int z) { ed[++cnt] = (edge){head[x], y, z}; head[x] = cnt; } int dep[300005], fa[300005][26], pre[300005]; inline void bfs() { queue <int> q; q.push(1); dep[0] = -1; dep[1] = 1; while(!q.empty()) { int x = q.front(); q.pop(); for (int i = head[x] ; i ; i = ed[i].nxt) { int to = ed[i].to; if (dep[to]) continue; pre[to] = i; dep[to] = dep[x] + 1; fa[to][0] = x; for (int j = 1 ; j <= 20 ; j ++) fa[to][j] = fa[fa[to][j-1]][j-1]; q.push(to); } } } inline int lca(int x, int y) { if (dep[x] < dep[y]) swap(x, y); for (int i = 20 ; i >= 0 ; i --) if (dep[fa[x][i]] >= dep[y]) x = fa[x][i]; if (x == y) return x; for (int i = 20 ; i >= 0 ; i --) if (fa[x][i] != fa[y][i]) x = fa[x][i], y = fa[y][i]; return fa[x][0]; } int qzh[300005]; void dfs(int x, int faa) { for (int i = head[x] ; i ; i = ed[i].nxt) { int to = ed[i].to; if (to == faa) continue; qzh[to] = qzh[x] + ed[i].val; dfs(to, x); } } struct path{ int u, v, dis, lca; }p[300005]; int top, maxdis; int cf[300005]; void efs(int x) { for (int i = head[x] ; i ; i = ed[i].nxt) { int to = ed[i].to; if (to == fa[x][0]) continue; efs(to); cf[x] += cf[to]; } if (cf[x] == top and ed[pre[x]].val >= maxdis) {ffl = 1;return ;} } inline bool check(int mid) { top = 0; maxdis = 0; ffl = 0; memset(cf, 0, sizeof cf); for (int i = 1 ; i <= m ; i ++) { if (p[i].dis > mid){ top++; cf[p[i].u]++, cf[p[i].v]++, cf[p[i].lca] -= 2; maxdis = max(maxdis, p[i].dis - mid); } } if (!top) return 1; efs(1); if(ffl) return 1; return 0; } int main() { n = read(), m = read(); for (int i = 1 ; i <= n - 1 ; i ++) { int x = read(), y = read(), z = read(); add(x, y, z), add(y, x, z); } bfs(); dfs(1, 0); int l = 0, r = 0; for (int i = 1 ; i <= m ; i ++) { p[i].u = read(), p[i].v = read(); p[i].lca = lca(p[i].u, p[i].v); p[i].dis = qzh[p[i].u] + qzh[p[i].v] - 2 * qzh[p[i].lca]; r = max(r, p[i].dis); } while(l <= r) { int mid = l + r >> 1; if (check(mid)) r = mid - 1, ans = mid; else l = mid + 1; } printf("%d\n", ans); return 0; }
$\sum_{age=16}^{18} hardworking = success$


 浙公网安备 33010602011771号
浙公网安备 33010602011771号