[CF453B] Little Pony and Harmony Chest
题意翻译
题目背景
暮暮正在公主两姐妹的城堡里研究和谐之元的宝箱。
题目描述
对于一个正整数序列bi，当且仅当它的任意两个元素都互质时，这个序列bi才是和谐的。据古书记载，宝箱的钥匙是能让以下表达式的值最小的和谐序列bi：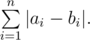
现在暮暮已经得到了序列ai，你能帮助暮暮找到开启宝箱的钥匙吗？
输入输出格式
输入格式：
第一行包含一个正整数 n (1 ≤ n ≤ 100) ——a、b序列的长度。
第二行包含一串长度为 n 的整数 a1, a2, ..., an (1 ≤ ai ≤ 30).
输出格式：
输出仅有一行——满足条件的bi序列。
题目描述
Princess Twilight went to Celestia and Luna's old castle to research the chest from the Elements of Harmony.
A sequence of positive integers bi b_{i} bi is harmony if and only if for every two elements of the sequence their greatest common divisor equals 1. According to an ancient book, the key of the chest is a harmony sequence bi b_{i} bi which minimizes the following expression:
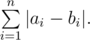You are given sequence ai a_{i} ai , help Princess Twilight to find the key.
输入输出格式
输入格式：
The first line contains an integer n n n ( 1<=n<=100 1<=n<=100 1<=n<=100 ) — the number of elements of the sequences a a a and b b b . The next line contains n n n integers a1,a2,...,an a_{1},a_{2},...,a_{n} a1,a2,...,an ( 1<=ai<=30 1<=a_{i}<=30 1<=ai<=30 ).
输出格式：
Output the key — sequence bi b_{i} bi that minimizes the sum described above. If there are multiple optimal sequences, you can output any of them.
输入输出样例
5 1 1 1 1 1
1 1 1 1 1
5 1 6 4 2 8
1 5 3 1 8
话说今天要求的4道题我做过3道...算了还是浪一吧...把昨天的题写一份题解。
我们首先可以确定，bi的范围一定是1~60。
然后我们数一数1~60的质数.
2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59才17个，而且59并不是必须的，因为选59不如选1更优。
所以我们可以状压一下，把质因子的使用情况状压一下。
设f[i][j]表示决策到了第i位，质因子使用情况是j的最小代价。
又因为还要输出方案，所以设lst[i][j]为f[i][j]最优时第i位选择的数字。
然后其他的就是普通到不能再普通的转移...
最后计算答案的时候特别巧妙(至少对于本蒟蒻来说)...
我们先找出来最优答案，记录下来最优答案的状态，然后倒着推
。每次的答案就是lst[i][j]，然后再把这个数字产生的影响从当前状态里去除，然后处理上一位...
简直666.学到了新的处理方式好开心...
有个小小的问题，为什么写着写着文字一块深一块浅...在线等
#include <iostream> #include <cstdio> #include <cstring> #include <bitset> using namespace std; inline int read(){ int res=0;char ch=getchar(); while(!isdigit(ch))ch=getchar(); while(isdigit(ch)){res=(res<<3)+(res<<1)+(ch^48);ch=getchar();} return res; } //2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59 inline int abss(int x){return x<0?-x:x;} int prime[]={0,2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53}; int f[105][1<<17], lst[105][1<<17]; int n, a[105]; int bin[20], sit[60]; int q[105]; int ans = 1e9; int main() { bin[0] = 1;for (int i = 1 ; i <= 19 ; i ++) bin[i] = bin[i-1] << 1; for (int i = 1 ; i <= 58 ; i ++) { for (int j = 1 ; j <= 16 ; j ++) if (i % prime[j] == 0) sit[i] += bin[j-1]; } n = read(); for (int i = 1 ; i <= n ; i ++) a[i] = read(); memset(f, 127, sizeof f); f[0][0] = 0; for (int i = 0 ; i < n ; i ++) { for (int j = 0 ; j <= (1<<16) - 1 ; j ++) { if (f[i][j] == 0x3f3f3f3f) continue; for (int k = 1 ; k <= 58 ; k ++) //枚举这一位填什么 { if ((j | sit[k]) != (j + sit[k])) continue;//这个数的质因子出现过，跳出 int t = f[i][j] + abss(k - a[i+1]); if (t < f[i+1][j+sit[k]]) { f[i+1][j+sit[k]] = t; lst[i+1][j+sit[k]] = k; } } } } int pos; for (int i = 0 ; i <= (1<<16) - 1 ; i ++) if (f[n][i] < ans) {ans = f[n][i], pos = i;} for (int i = n ; i >= 1 ; i --) { q[i] = lst[i][pos]; pos -= sit[q[i]]; } for (int i = 1 ; i <= n ; i ++) printf("%d ", q[i]); return 0; }
