过山车（二分图匹配裸题） HDU - 2063

RPG girls今天和大家一起去游乐场玩，终于可以坐上梦寐以求的过山车了。可是，过山车的每一排只有两个座位，而且还有条不成文的规矩，就是每个女生必须找个个男生做partner和她同坐。但是，每个女孩都有各自的想法，举个例子把，Rabbit只愿意和XHD或PQK做partner，Grass只愿意和linle或LL做partner，PrincessSnow愿意和水域浪子或伪酷儿做partner。考虑到经费问题，boss刘决定只让找到partner的人去坐过山车，其他的人，嘿嘿，就站在下面看着吧。聪明的Acmer，你可以帮忙算算最多有多少对组合可以坐上过山车吗？

Input输入数据的第一行是三个整数K , M , N，分别表示可能的组合数目，女生的人数，男生的人数。0<K<=1000
1<=N 和M<=500.接下来的K行，每行有两个数，分别表示女生Ai愿意和男生Bj做partner。最后一个0结束输入。Output对于每组数据，输出一个整数，表示可以坐上过山车的最多组合数。

Sample Input

6 3 3
1 1
1 2
1 3
2 1
2 3
3 1
0

Sample Output

3

 

分析：二分图匹配经典的匈牙利算法。

首先介绍一下二分图以及匈牙利算法。

二分图又称作二部图，是图论中的一种特殊模型。 设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边（i，j）所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B)，则称图G为一个二分图。

简单的说，一个图被分成了两部分，相同的部分没有边，那这个图就是二分图，二分图是特殊的图。

匈牙利算法几乎是二分图匹配的核心算法，除了二分图多重匹配外均可使用

注：以下转自 http://blog.csdn.net/dark_scope/article/details/8880547

匈牙利算法是由匈牙利数学家Edmonds于1965年提出，因而得名。匈牙利算法是基于Hall定理中充分性证明的思想，它是部图匹配最常见的算法，该算法的核心就是寻找增广路径，它是一种用增广路径求二分图最大匹配的算法。

-------等等，看得头大？那么请看下面的版本：

 

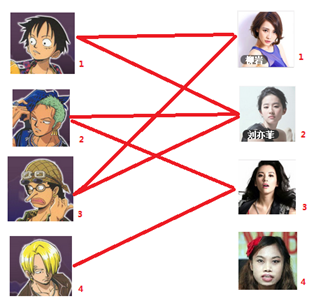
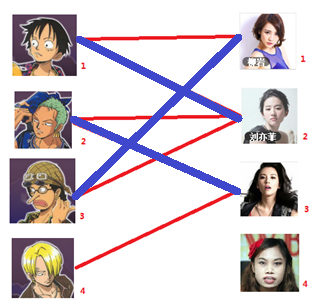
通过数代人的努力，你终于赶上了剩男剩女的大潮，假设你是一位光荣的新世纪媒人，在你的手上有N个剩男，M个剩女，每个人都可能对多名异性有好感（-_-||暂时不考虑特殊的性取向），如果一对男女互有好感，那么你就可以把这一对撮合在一起，现在让我们无视掉所有的单相思（好忧伤的感觉），你拥有的大概就是下面这样一张关系图，每一条连线都表示互有好感。

 

本着救人一命，胜造七级浮屠的原则，你想要尽可能地撮合更多的情侣，匈牙利算法的工作模式会教你这样做：

===============================================================================

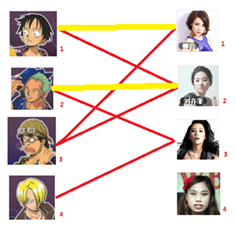
一： 先试着给1号男生找妹子，发现第一个和他相连的1号女生还名花无主，got it，连上一条蓝线

 

===============================================================================

二：接着给2号男生找妹子，发现第一个和他相连的2号女生名花无主，got it

 

===============================================================================

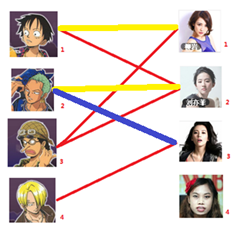
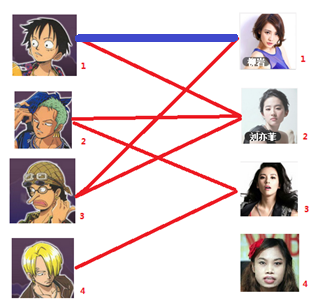
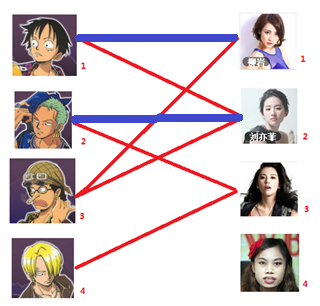
三：接下来是3号男生，很遗憾1号女生已经有主了，怎么办呢？

我们试着给之前1号女生匹配的男生（也就是1号男生）另外分配一个妹子。

 

(黄色表示这条边被临时拆掉)

 

与1号男生相连的第二个女生是2号女生，但是2号女生也有主了，怎么办呢？我们再试着给2号女生的原配()重新找个妹子(注意这个步骤和上面是一样的，这是一个递归的过程)

 

 

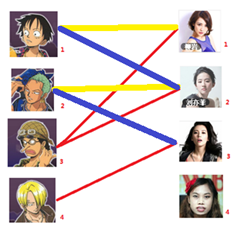
此时发现2号男生还能找到3号女生，那么之前的问题迎刃而解了，回溯回去

 

2号男生可以找3号妹子~~~                  1号男生可以找2号妹子了~~~                3号男生可以找1号妹子

所以第三步最后的结果就是：

 

===============================================================================

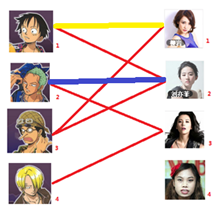
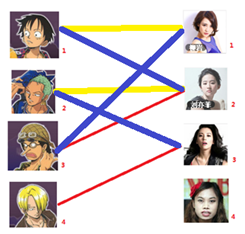
四： 接下来是4号男生，很遗憾，按照第三步的节奏我们没法给4号男生腾出来一个妹子，我们实在是无能为力了……香吉士同学走好。

 

===============================================================================

这就是匈牙利算法的流程，其中找妹子是个递归的过程，最最关键的字就是“腾”字

其原则大概是：有机会上，没机会创造机会也要上

因此从题意上就可以看出这是一道裸题，另外，像说明一下代码中girl数组的含义girl[i]代表了i这个男生选择的女生是谁。

AC代码：

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn = 505;
#define LL long long
#define iNF 0x3f3f3f3f
int k,n,m;
int line[maxn][maxn];
int girl[maxn],vis[maxn];

bool found(int x){
    for(int i=1;i<=n;i++){
        if(line[x][i]&&!vis[i]){
            vis[i]=1;
            if(girl[i]==0||found(girl[i])){
                girl[i]=x;
                return 1;
            }
        }
    }
    return 0;
}

int main(){
   int x,y;
    while(scanf("%d",&k)&&k){
        scanf("%d%d",&m,&n);
        memset(line,0,sizeof(line));
        memset(girl,0,sizeof(girl));
        for(int i=0;i<k;i++){
            scanf("%d%d",&x,&y);
            line[x][y]=1;
        }
        int sum=0;
        for(int i=1;i<=m;i++){
            memset(vis,0,sizeof(vis));
            if(found(i)) sum++;
        }
        printf("%d\n",sum);
    }



    return 0;
}