剪格子---（dfs回溯）

如图p1.jpg所示，3 x 3 的格子中填写了一些整数。

我们沿着图中的红色线剪开，得到两个部分，每个部分的数字和都是60。

本题的要求就是请你编程判定：对给定的m x n 的格子中的整数，是否可以分割为两个部分，使得这两个区域的数字和相等。

如果存在多种解答，请输出包含左上角格子的那个区域包含的格子的最小数目。 如果无法分割，则输出 0

程序输入输出格式要求：
程序先读入两个整数 m n 用空格分割 (m,n<10)
表示表格的宽度和高度
接下来是n行，每行m个正整数，用空格分开。每个整数不大于10000
程序输出：在所有解中，包含左上角的分割区可能包含的最小的格子数目。

例如：
用户输入：
3 3
10 1 52
20 30 1
1 2 3

则程序输出：
3

再例如：
用户输入：
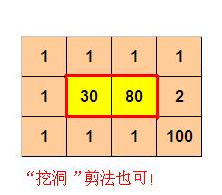
4 3
1 1 1 1
1 30 80 2
1 1 1 100

则程序输出：
10

(参见p2.jpg)

资源约定：
峰值内存消耗 < 64M
CPU消耗 < 5000ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入...” 的多余内容。

所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。

注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准，不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include ， 不能通过工程设置而省略常用头文件。

提交时，注意选择所期望的编译器类型。

分析：dfs回溯+搜索+是否选择当前格子

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
#define INF 0x3f3f3f3f

int dr[4][2]={{0,1},{0,-1},{1,0},{-1,0}};/*方向*/
int all=0;
int ans=INF;
int n,m;
int a[15][15];/*记录格子权值*/
int vst[15][15];/*记录这个格子是否被占据*/

bool in(int x,int y){/*判断此坐标是否在格子之中*/
    return x>=0&&x<n&&y>=0&&y<m;
}

void dfs(int sum,int cnt,int x,int y){
    if(sum*2>all) return ;
    else if(sum*2==all){
        if(ans>cnt){/*因为从左上角格子开始走的，所以左上角格子必选，只需要判断ans与cnt的大小就可以了*/
            ans=cnt;
        }
        return ;
    }
    vst[x][y]=1;/*标记占据这个格子*/
    for( int i=0; i<4; i++ ){
        int tx=x+dr[i][0];
        int ty=y+dr[i][1];
        if(in(tx,ty)&&!vst[tx][ty]){
            dfs(sum+a[x][y],cnt+1,tx,ty);
        }
    }
    vst[x][y]=0;/*回溯*/
}

int main(int argc, char const *argv[])
{
    cin>>m>>n;
    memset(vst,0,sizeof(vst));
    for(int i=0; i<n; i++ ){
        for( int j=0; j<m; j++ ){
            scanf("%d",&a[i][j]);
            all+=a[i][j];
        }
    }
    dfs(0,0,0,0);
    if(ans==INF) cout<<0<<endl;
    else cout<<ans<<endl;

    return 0;
}