数据结构图之三（最短路径--迪杰斯特拉算法）
【1】最短路径
最短路径？别乱想哈，其实就是字面意思，一个带边值的图中从某一个顶点到另外一个顶点的最短路径。
官方定义：对于内网图而言，最短路径是指两顶点之间经过的边上权值之和最小的路径。
并且我们称路径上的第一个顶点为源点，最后一个顶点为终点。
由于非内网图没有边上的权值，所谓的最短路径其实是指两顶点之间经过的边数最少的路径。
别废话了！整点实际的哈，你能很快计算出下图中由源点V0到终点V8的最短路径吗？
【2】迪杰斯特拉算法
迪杰斯特拉算法是按路径长度递增的次序产生最短路径的思路求解。
具体算法及其详细讲解如下：
阅读程序前，先要搞明白几个数组作用：
final[w]=1; 表示V0到Vw顶点已经有最短路径的结果
ShortPathTable[w]; 表示V0到Vw顶点的最短路径权值和
Pathmatirx[w]; 表示V0到Vw顶点的前驱顶点下标值
开始调用算法前，我们需要为案例图创建邻接矩阵图，如下所示：
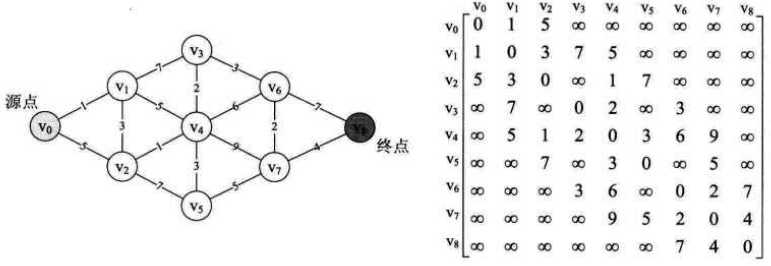
（1）程序开始运行，final数组是为了标记V0到某顶点是否已经求得最短路径。
如果V0到Vw已经有结果，那么final[w]=1;
（2）第5~10行，是对数据初始化工作。 此时final数组均赋值为0，表示所有点均未求得最短路径。
D数组为 {0,1,5,65515,65535,65535,65535,65535,65535}。因为V0与V1和V2的边权值为1和5。
P数组全为0，表示目前没有路径。
（3）第11行，表示V0至V0路径为0。
第12行，表示V0点到V0点已经求得最短路径，因此final[0]=1。
此时final数组为 {1,0,0,0,0,0,0,0,0}，此时整个初始化工作完成。
（4）第13~33行为主循环，每次循环求得V0与一个顶点的最短路径。除去V0，因此索引从1开始。
（5）第15~23行，先令min为65535的极大值，通过w控制循环，与D[w]比较找到最小值为min=1，同时确定k=1。
（6）第24行，由k=1可知与V0最近的顶点是V1，并且由D[1]=1知道此时V0到V1的最短路径是1。
因此再将对应的final[1]设置为1。此时final数组为 {1,1,0,0,0,0,0,0,0}
（7）第25~32行是一循环，此循环甚为关键。
它的目的是在刚才已经找到V0与V1的最短路径基础之上，对V1与其它顶点的边进行计算，得到V0与它们的当前最短距离，如图所示：
因为min=1,所以D[2]=5不再是V0到V2的最短路径，现在D[2]=V0->V1->V2=min+3=4, D[3]=V0->V1->V3=min+7=8,
D[4]=V0->V1->V4=min+5=6，于是D数组当前值为 {0,1,4,8,6,65535,65535,65535,65535}。
而P[2]=1，P[3]=1，P[4]=1，其表示V0到V2，V3，V4点的最短路径它们的前驱均是V1。
此时P数组为 {0,0,1,1,1,0,0,0,0}。
（8）新一轮循环，此时i=2。第15~23行，对w循环，注意因为final[0]=1和final[1]=1，由第18行的！final[w]可知：
V0与V1并不参与最小值的获取。通过循环比较，找到最小值min=4，k=2。
（9）第24行，由k=2，表示已经求出V0到V2的最短路径，并且由D[2]=4知道最短路径距离为4。
因此将V2对应的final[2]设置为1，此时final数组为 {1,1,1,0,0,0,0,0,0}。
（10）第25~32行，在刚才已经找到V0与V2的最短路径的基础上，对V2与其它顶点的边进行计算，得到V0与它们的最短距离。
如图所示：
因为min=4，所以D[4]=6不再是V0到V4的最短距离，现在D[4]=V0->V2->V4=min+1=5，D[5]=V0->V2->V5=min+7=11。
因此D数组当前值为 {0,1,4,8,5,11,65535,65535,65535,65535}。
而原本P[4]=1，此时P[4]=2，P[5]=2，它表示的意思是V0到V4和V5的最短路径前驱均为V2。
此时P数组为 {0,0,1,1,2,2,0,0,0}。
（11）重新再开始一轮循环，此时i=3。第15~23行，通过对w循环比较找到最小值min=5，k=4。
（12）第24行，由k=4表示已经求出V0到V4的最短路径，并且由D[4]=5知道最短路径距离为5。
因此将V4对应的final[4]设置为1。此时final数组为 {1,1,1,0,1,0,0,0,0}。
（13）第25~32行，对V4与其它顶点的边值进行计算，得到V0与它们的当前最短距离，如图所示：
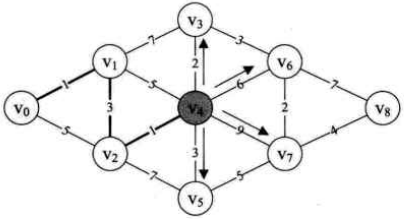
因为min=5，所以D[3]=8不再是V0到V3的最短路径，现在D[3]=V0->V4->V3=min+2=7，同理：
D[5]=V0->V4->V5=min+3=8，D[6]=V0->V4->V6=min+6=11，
D[7]=V0->V4->V7=min+9=14，因此，D数组当前值为 {0,1,4,7,5,8,11,14,65535}。
而原本P[3]=1，此时P[3]=4，原本P[5]=2，此时P[5]=4。
另外P[6]，P[7]=4，它表示V0到V3，V5，V6，V7点的最短路径它们的前驱是V4。
此时P数组值为 {0,0,1,4,2,4,4,4,0}。
（14）之后的循环完全类似。得到最终的结果，如图所示：
此时final数组为 {1,1,1,1,1,1,1,1,1}，它表示所有的顶点均完成了最短路径的查找工作。
此时D数组为 {0,1,4,7,5,8,10,12,16}，它表示V0到各个顶点的最短路径数，比如D[8]=1+3+1+2+3+2+4=16。
此时的P数组为 {0,0,1,4,2,4,3,6,7}：
这个P数组值可能难理解一些。比如P[8]=7，它表示要查看V0到V8的最短路径时，顶点V8的前驱是V7；
再由P[7]=6表示要查看V0到V7的最短路径时，顶点V7的前驱是V6，同理，P[6]=3表示V6的前驱是V3。
这样就可以得到：V0到V8最短路径为V8<-V7<-V6<-V3<-V4<-V2<-V1<-V0
即就是： V0->V1->V2->V4->V3->V6->V7->V8。
【3】算法实现
实现代码如下：
1 #include <iostream> 2 #include "SeqList.h" 3 #include "Stack.h" 4 #include <iomanip> 5 using namespace std; 6 7 #define INFINITY 65535 8 9 template<class NameType, class DistType> 10 class Graph 11 { 12 private: 13 SeqList<NameType> Vertices; 14 DistType **Edges; 15 int nVer, nEdges; 16 17 public: 18 Graph() 19 : Edges(NULL) 20 , nEdges(0) 21 , nVer(0) 22 {} 23 ~Graph() 24 {} 25 26 public: 27 int GetVer() const 28 { 29 return nVer; 30 } 31 32 istream & operator>>(istream &in) 33 { 34 int v, u, value; 35 int i, j; 36 NameType item; 37 cout << "请输入顶点的个数: " << endl; 38 in >> nVer; 39 cout << "请输入顶点的数据信息: " << endl; 40 for (i = 0; i < nVer; ++i) 41 { 42 in >> item; 43 Vertices.push_back(item); // 保存全部顶点 44 } 45 /////二维数组的创建并初始化 46 Edges = new DistType*[nVer]; // DistType *ar[10]; 47 for (i = 0; i < nVer; ++i) 48 { 49 Edges[i] = new DistType[nVer]; 50 for (j = 0; j < nVer; ++j) 51 { 52 Edges[i][j] = 0; 53 } 54 } 55 cout << "请输入边的个数: " << endl; 56 in >> nEdges; 57 cout << "请输入边的信息：" << endl; 58 for (i = 0; i < nEdges; ++i) 59 { 60 in >> v >> u >> value; 61 Edges[v][u] = value; 62 Edges[u][v] = value; 63 } 64 return in; 65 } 66 ostream & operator<<(ostream &out) const 67 { 68 int i, j; 69 out << "顶点信息 " << endl; 70 for (i = 1; i <= nVer; ++i) 71 { 72 out << Vertices[i] << setw(5); 73 } 74 out << endl; 75 out << "矩阵信息：" << endl; 76 out << setw(10); 77 for (i = 1; i <= nVer; ++i) 78 { 79 out << Vertices[i] << setw(5); 80 } 81 out << endl; 82 for (i = 0; i < nVer; ++i) 83 { 84 out << Vertices[i+1] << setw(5); 85 for (j = 0; j < nVer; ++j) 86 { 87 if (0 == Edges[i][j] && i != j) 88 Edges[i][j] = INFINITY; 89 cout << Edges[i][j] << setw(5); 90 } 91 out << endl; 92 } 93 out << endl; 94 95 return out; 96 } 97 // 迪杰斯特拉算法实现 98 void ShortestPath_Dijkstra(int v0, int* final, int*p, int *D) 99 { 100 int v, w, k, min; 101 // 初始化数据 102 for (v = 0; v < nVer; ++v) 103 { 104 final[v] = 0; // 全部顶点初始化为未知对短路径状态 105 D[v] = Edges[v0][v]; //将与V0点有连线的顶点加上权值 106 p[v] = 0; // 初始化路径数组p为0 107 } 108 D[v0] = 0; // V0至V0路径为0 109 final[v0] = 1; // final[W]=1表示V0至V0不需要求路径 110 // 开始主循环，每次求得V0到某个V顶点的最短路径 111 for (v = 1; v < nVer; ++v) 112 { 113 min = INFINITY; // 当前所知离V0顶点最近距离 114 for (w = 0; w < nVer; ++w) // 寻找离V0最近的顶点 115 { 116 if (!final[w] && D[w] < min) 117 { 118 min = D[w]; // w顶点离V0顶点更近 119 k = w; 120 } 121 } 122 123 final[k] = 1; // 将目前找到的最近的顶点置为1 124 for (w = 0; w < nVer; ++w) // 修正当前最短路径距离 125 { 126 // 如果经过V顶点的路径比现在这条路径的长度短的话 127 if (!final[w] && (min + Edges[k][w] < D[w])) 128 { 129 // 说明找到了最短的路径，修改D[w] 和 p[w] 130 D[w] = min + Edges[k][w]; // 修改当前路径长度 131 p[w] = k; 132 } 133 } 134 } 135 } 136 }; 137 138 template<class NameType, class DistType> 139 istream & operator>>(istream &in, Graph<NameType,DistType> &g) 140 { 141 g >> in; 142 return in; 143 } 144 145 template<class NameType, class DistType> 146 ostream & operator<<(ostream &out, const Graph<NameType,DistType> &g) 147 { 148 g << out; 149 return out; 150 } 151 152 void main() 153 { 154 Graph<char, int> myg; 155 cin >> myg; 156 cout << "打印所有输入信息：" << endl; 157 cout << myg << endl; 158 cout << "求最短路径....." << endl; 159 int numVer = myg.GetVer(); 160 int* pFinal = new int[numVer]; 161 int* pPathmatirx = new int[numVer]; 162 int* pShortPath = new int[numVer]; 163 myg.ShortestPath_Dijkstra(0, pFinal, pPathmatirx, pShortPath); 164 cout << "打印各顶点最短路径标记数组值：" << " "; 165 for (int i = 0; i < numVer; ++i) 166 { 167 cout << pFinal[i] << " "; 168 } 169 cout << endl; 170 cout << "打印最短路径数组值：" << " "; 171 for (int i = 0; i < numVer; ++i) 172 { 173 cout << pShortPath[i] << " "; 174 } 175 cout << endl; 176 cout << "打印最短路径前驱数组值：" << " "; 177 for (int i = 0; i < numVer; ++i) 178 { 179 cout << pPathmatirx[i] << " "; 180 } 181 cout << endl; 182 cout << "打印V0到各个顶点最短路径值以及路径信息：" << endl; 183 SeqStack<int> sQ; 184 for (int i = 1; i < numVer; ++i) 185 { 186 cout << "V0~V" << i << ": " << pShortPath[i] << endl; 187 188 sQ.Push(pPathmatirx[i]); 189 int n = 0; 190 while (sQ.GetTop(n) && n != 0) 191 { 192 sQ.Push(pPathmatirx[n]); 193 } 194 195 while (!sQ.IsEmpty()) 196 { 197 int m = 0; 198 sQ.Pop(m); 199 cout << "V" << m << "->"; 200 } 201 cout << "V" << i << endl; 202 } 203 delete []pFinal; 204 delete []pPathmatirx; 205 delete []pShortPath; 206 pFinal = NULL; 207 pPathmatirx = NULL; 208 pShortPath = NULL; 209 } 210 // 备注： 211 // 最短路径迪杰斯特拉算法实现 212 // 整理于2013-12-04 213 // 测试输入程序为： 214 /* 215 请输入顶点的个数: 216 9 217 请输入顶点的数据信息: 218 A B C D E F G H I 219 请输入边的个数: 220 16 221 请输入边的信息： 222 0 1 1 223 0 2 5 224 1 2 3 225 1 3 7 226 1 4 5 227 2 4 1 228 2 5 7 229 3 4 2 230 3 6 3 231 4 5 3 232 4 6 6 233 4 7 9 234 5 7 5 235 6 7 2 236 6 8 7 237 7 8 4 238 打印所有输入信息： 239 顶点信息 240 A B C D E F G H I 241 矩阵信息： 242 A B C D E F G H I 243 A 0 1 5655356553565535655356553565535 244 B 1 0 3 7 565535655356553565535 245 C 5 3 065535 1 7655356553565535 246 D65535 765535 0 265535 36553565535 247 E65535 5 1 2 0 3 6 965535 248 F6553565535 765535 3 065535 565535 249 G655356553565535 3 665535 0 2 7 250 H65535655356553565535 9 5 2 0 4 251 I655356553565535655356553565535 7 4 0 252 253 254 求最短路径..... 255 打印各顶点最短路径标记数组值： 1 1 1 1 1 1 1 1 1 256 打印最短路径数组值： 0 1 4 7 5 8 10 12 16 257 打印最短路径前驱数组值： 0 0 1 4 2 4 3 6 7 258 打印V0到各个顶点最短路径值以及路径信息： 259 V0~V1: 1 260 V0->V1 261 V0~V2: 4 262 V0->V1->V2 263 V0~V3: 7 264 V0->V1->V2->V4->V3 265 V0~V4: 5 266 V0->V1->V2->V4 267 V0~V5: 8 268 V0->V1->V2->V4->V5 269 V0~V6: 10 270 V0->V1->V2->V4->V3->V6 271 V0~V7: 12 272 V0->V1->V2->V4->V3->V6->V7 273 V0~V8: 16 274 V0->V1->V2->V4->V3->V6->V7->V8 275 */
关于实现代码中的SeqList.h文件和Stack.h文件从随笔《顺序表》和《栈》中查找拷贝一份即可。调试环境为VS2010。
Good Good Study, Day Day Up.
顺序 选择 循环 总结
