二叉树存储

特殊二叉树

满二叉树（Full Binary Tree）

除了叶子节点，每一个节点都有两个子节点。（深度为k。节点数量为2^k-1个）。

完全二叉树（Complete Binary Tree)

有n个结点的二叉树，对树中结点按 从上至下、从左到右顺序进行编号， 编号为i（1 ≤ i ≤ n）结点与满二叉树 中编号为 i 结点在二叉树中位置相同。

下面个这个是完全二叉树

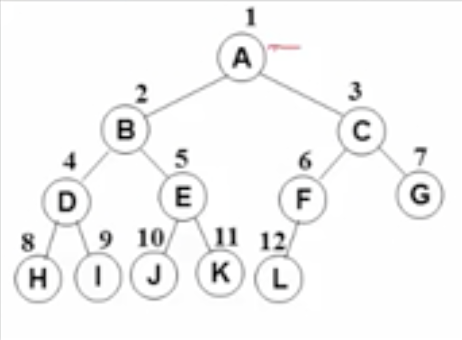
下面这个不是完全二叉树

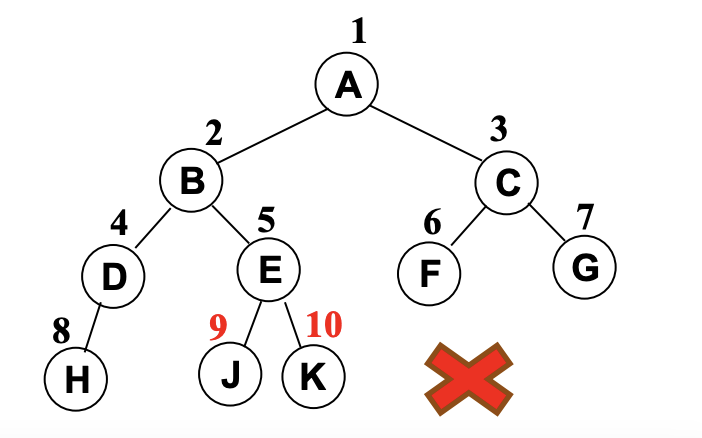
汇总例子

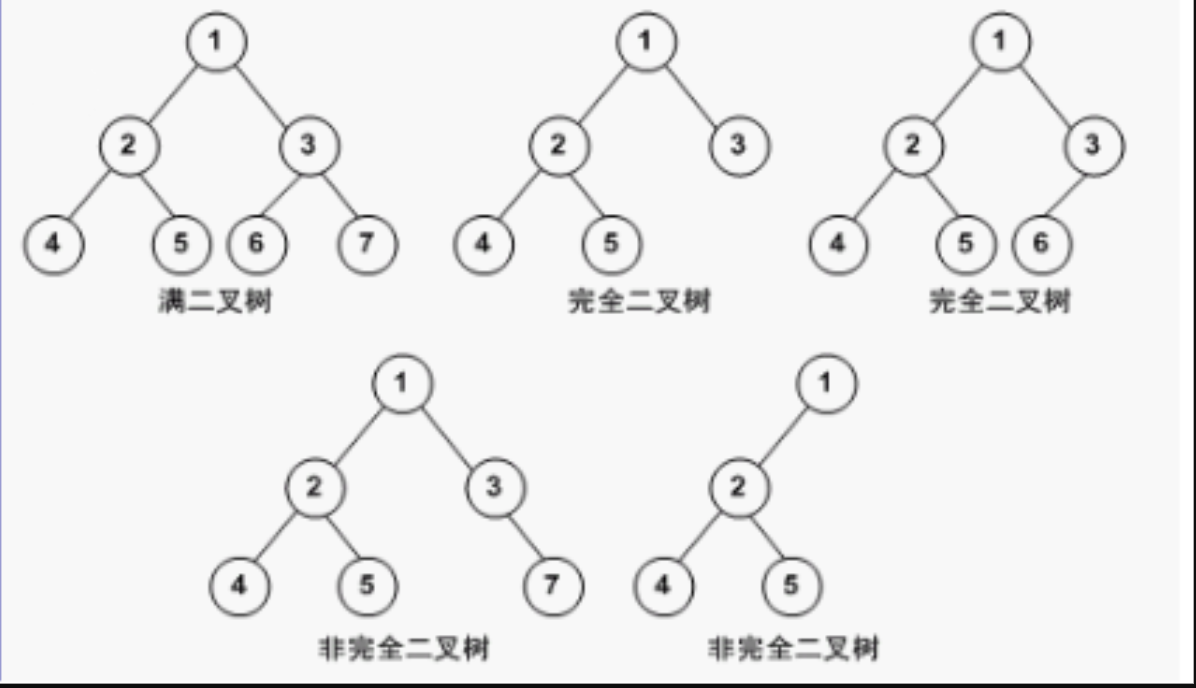
二叉树存储

数组存储

对于完全二叉树，从上至下，从左到右依次存储在数组中。

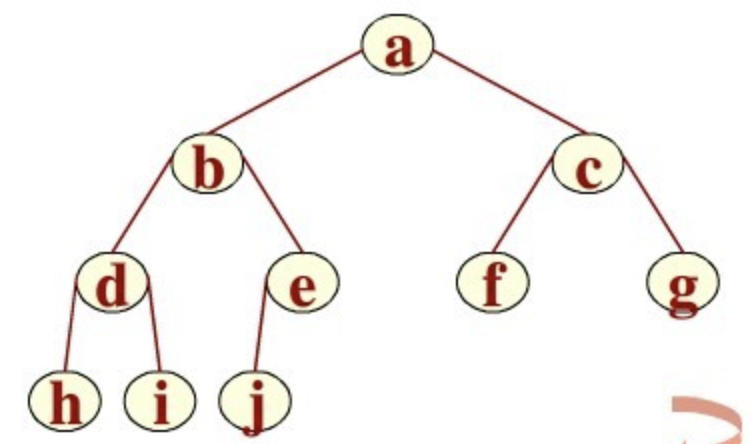
item	a	b	c	d	e	f	g	h	i	j
index	0	1	2	3	4	5	6	7	8	9

那么如何通过数组找出树之间的关系呢。

第n个元素的左子节点为 2 * n + 1
第n个元素的右子节点为 2 * n + 2
第n个元素的父节点为 (n-1) / 2

n表示数组的下标。

非完全二叉树其实也可以用以上的方式进行存储，只需要对缺失的节点补空，模拟一个完全二叉树。但是如果非完全二叉树平衡度极低，会浪费大量的存储空间。

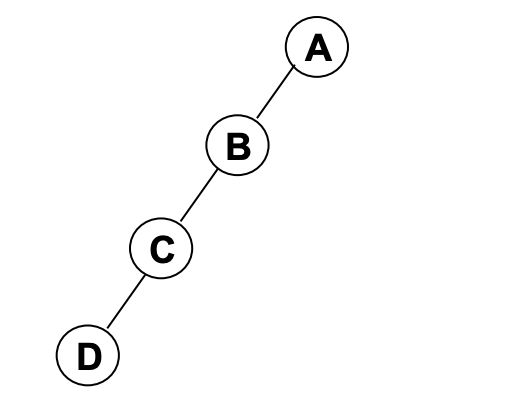
item	A	B	NULL	C	NULL	NULL	NULL	D
index	0	1	2	3	4	5	6	7

可以看到，这种情况下，浪费了一半的空间。

完全二叉树的引入，某种程度上就是为了解决空间浪费问题。

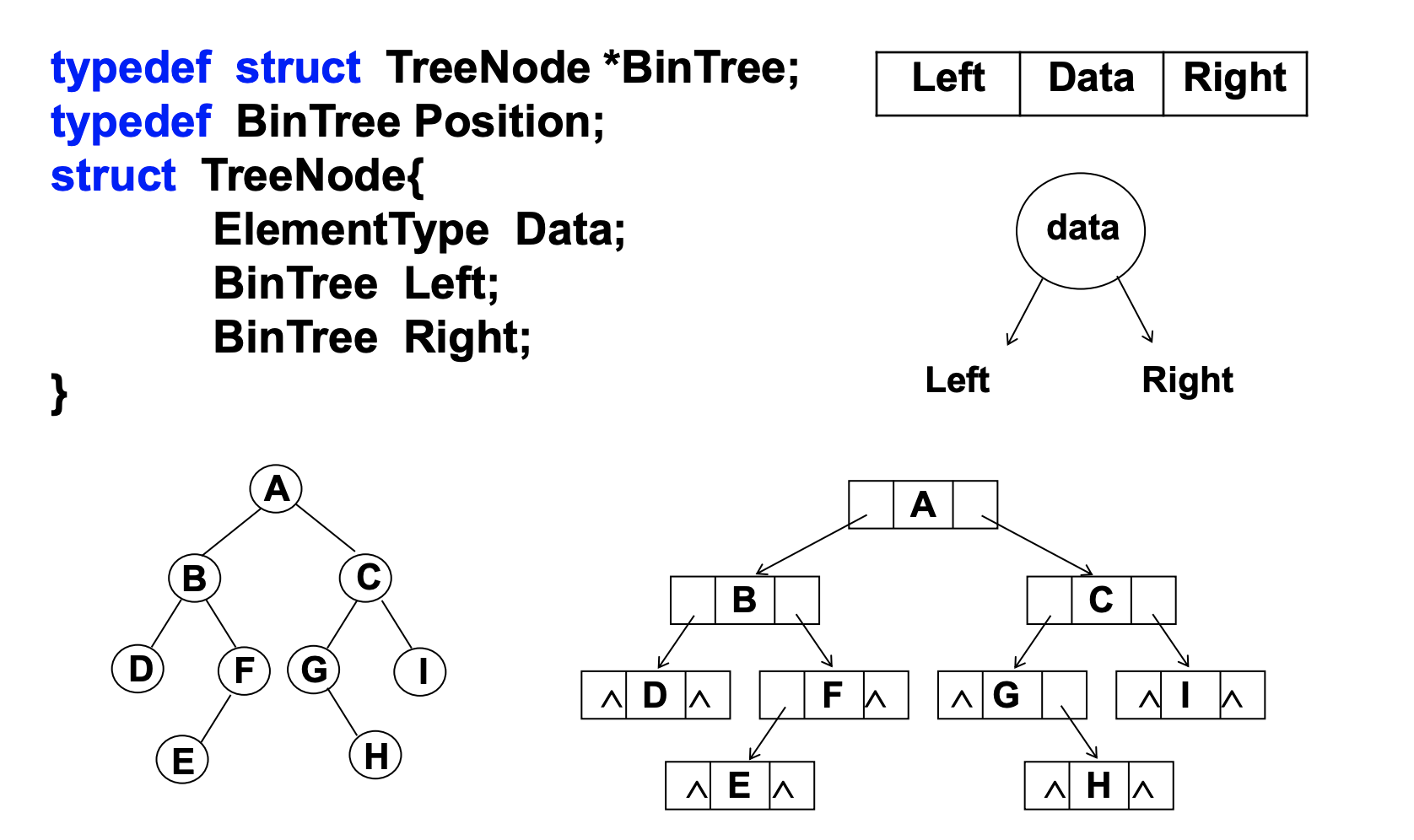
链式存储