利用百度地图API和群蚁算法,对TSP问题进行模拟与求解
前言
最近由于换了工作,期间也有反思和总结上家公司的得失,总觉得有什么事情当初可以完成或者完成得更好,其中TSP问题就是其中之一。当初在开发一个仓配系统的时候,有一个线路排程的需求,当时自己简单在纸上画了思路,发现求精确解算法复杂度是N!,所以去百度,发现了NPC问题的概念,但是一直以来都没有对这个问题好好研究过,最终只是选择了贪心算法这一求近似解的方案,正好这是我的第一篇博客,就拿这个“遗憾”开刀吧。
1、 利用百度地图API模拟TSP的各个城市点
1.1、 调用百度地图API解析经纬度
这里首先到百度地图API官网申请一个apiKey,调地址解析接口会使用到,其中地址解析接口的参数可以访问http://lbsyun.baidu.com/index.php?title=uri/api/web开查看,这里我先将它截图:

将示例中的url(这里的output我采用json)在浏览器中输入,会得到如下结果:
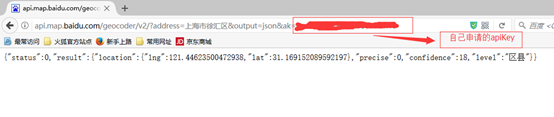
这里利用HttpRequest方法来调用地址解析接口,类似于爬虫,最后将结果反序列化为实体类,代码如下:
///地址解析结果的实体类

using System; using System.Collections.Generic; using System.Linq; using System.Text; namespace Entity.BaiduEntity { public class MapInfo { public int Status { get; set; } public Result Result { get; set; } } public class Result { public Location Location { get; set; } public int Precise { get; set; } public int Confidence { get; set; } public string Level { get; set; } } public class Location { public double Lng { get; set; } public double Lat { get; set; } } }
///利用HttRequest调用API接口

using Entity.BaiduEntity; using Newtonsoft.Json; using System; using System.Collections.Generic; using System.IO; using System.Linq; using System.Net; using System.Text; using System.Web; namespace BLL.BaiduMap { public class BaiduApiHandle { public static MapInfo GetLngAndLat(string address) { //自己到官网申请 string apiKey = "申请到的apiKey"; string postData = string.Format("address={0}&output={1}&ak={2}", address, "json", apiKey); string url = "http://api.map.baidu.com/geocoder/v2/"; //string url = "http://api.map.baidu.com/geocoder/v2/?address=" + address + "&output=json&ak=" + apiKey; byte[] arrs = Encoding.GetEncoding("UTF-8").GetBytes(postData); HttpWebRequest request = (HttpWebRequest)System.Net.WebRequest.Create(url); request.Referer = url; request.UserAgent = "Mozilla/4.0 (compatible; MSIE 6.0; Windows NT 5.1; SV1; .NET CLR 2.0.50727; .NET CLR 3.0.04506.648; .NET CLR 3.0.4506.2152; .NET CLR 3.5.30729)"; request.Accept = "*/*"; request.Method = "Post"; request.ContentLength = Convert.ToInt64(arrs.Length.ToString()); request.ContentType = "application/x-www-form-urlencoded"; Stream reqstream = request.GetRequestStream(); reqstream.Write(arrs, 0, arrs.Length); request.Timeout = 30 * 1000;//每一个请求30秒延迟,超过30秒不予操作。 WebResponse wResp = request.GetResponse(); Stream respStream = wResp.GetResponseStream(); StreamReader reader = new StreamReader(respStream, Encoding.GetEncoding("UTF-8")); string result = reader.ReadToEnd(); reqstream.Dispose(); respStream.Dispose(); reader.Dispose(); MapInfo mapInfo = JsonConvert.DeserializeObject<MapInfo>(result); //因为output参数是json,所以这里用Newtonsoft.Json进行反序列化 return mapInfo; } } }
1.2、利用经纬度计算两个地址间的距离
其实这个网上有大量雷同的计算方法,但是这个方法是我很久以前引用过来的,原出处已经翻不到了,只好在这里点出此算法非我原创,若有幸让原作者看到,请通知我注明出处。这里我先简单的介绍一下算法思路,以地球的球心作为坐标系原点作一个三维坐标系,如图:

其中坐标A(x1,y1,z1),坐标B(x2,y2,z2),注意一下,其中x=r*sinɵ*cosɸ,y=r* r*sinɵ*sinɸ,z=r*cos ɵ,这里将角度转化为π来计算,让经纬度*π/180,那么坐标点在北纬时:ɵ=π/2-纬度*π/180;坐标点在南纬时:ɵ=π/2+纬度*π/180;坐标点在西经时:ɸ=π*2-经度*π/180;这个换算完成后,就可以通过给(x1-x2)^2+(y1-y2)^2+(z1-z2)^2开方计算出两点间的直线距离d,然后通过余弦定理求两点之间的夹角,最后计算出两点之间的球面距离,代码如下:

using System; using System.Collections.Generic; using System.Linq; using System.Text; namespace BLL.BaiduMap { public class DistinceCalculate { private static double EARTH_RADIUS = 6378137;//赤道半径(单位m) public static double LantitudeLongitudeDist(double lon1, double lat1, double lon2, double lat2) { double radLat1 = rad(lat1); double radLat2 = rad(lat2); double radLon1 = rad(lon1); double radLon2 = rad(lon2); if (radLat1 < 0) radLat1 = Math.PI / 2 + Math.Abs(radLat1);// south if (radLat1 > 0) radLat1 = Math.PI / 2 - Math.Abs(radLat1);// north if (radLon1 < 0) radLon1 = Math.PI * 2 - Math.Abs(radLon1);// west if (radLat2 < 0) radLat2 = Math.PI / 2 + Math.Abs(radLat2);// south if (radLat2 > 0) radLat2 = Math.PI / 2 - Math.Abs(radLat2);// north if (radLon2 < 0) radLon2 = Math.PI * 2 - Math.Abs(radLon2);// west double x1 = EARTH_RADIUS * Math.Cos(radLon1) * Math.Sin(radLat1); double y1 = EARTH_RADIUS * Math.Sin(radLon1) * Math.Sin(radLat1); double z1 = EARTH_RADIUS * Math.Cos(radLat1); double x2 = EARTH_RADIUS * Math.Cos(radLon2) * Math.Sin(radLat2); double y2 = EARTH_RADIUS * Math.Sin(radLon2) * Math.Sin(radLat2); double z2 = EARTH_RADIUS * Math.Cos(radLat2); double d = Math.Sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2) + (z1 - z2) * (z1 - z2)); //余弦定理求夹角 double theta = Math.Acos((EARTH_RADIUS * EARTH_RADIUS + EARTH_RADIUS * EARTH_RADIUS - d * d) / (2 * EARTH_RADIUS * EARTH_RADIUS)); double dist = theta * EARTH_RADIUS; return dist; } private static double rad(double d) { return d * Math.PI / 180.0; } } }
2、 通过群蚁算法求最短路径的近似解
关于群蚁算法,网上的介绍也有很多,不过偷下懒,只关注了C#的实现,这里参考的是园子里数据之巅的群蚁算法理论与实践全攻略——旅行商等路径优化问题的新方法 ,我就指出我对这篇文章理解起来比较费力的几点吧。
(1)这里的轮盘赌注法是遗传算法的一种思路,即通过产生一个随机数来选择下一个访问的城市,可以把0.081、0.74、0.18视为[0,0.081],[0.081,0.821],[0.821,1]这么三个区间,然后产生一个0到1的随机数(保留两位有效小数),当这个随机小数属于区间[0,0.081]时,选择城市B,属于[0.081,0.821]时,选择城市C,属于[0.821,1]时,选择城市D。这里是对群蚁算法的一种优化,优化方式有多种,可以自行查阅资料。

(2)代码处关于List的深复制
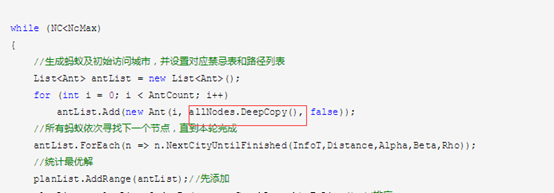
这个原作者没有给出实现,我用拓展方法实现了一下,代码如下:

using System.IO; using System.Linq; using System.Reflection; using System.Text; using System.Xml.Serialization; namespace Entity { public static class ExpandClass { public static List<T> DeepCopy<T>(this List<T> list) { return DeepCopyWithXmlSerializer(list); } // 利用XML序列化和反序列化实现 private static T DeepCopyWithXmlSerializer<T>(T obj) { object retval; using (MemoryStream ms = new MemoryStream()) { XmlSerializer xml = new XmlSerializer(typeof(T)); xml.Serialize(ms, obj); ms.Seek(0, SeekOrigin.Begin); retval = xml.Deserialize(ms); ms.Close(); } return (T)retval; } //public object Clone() //{ // return this.MemberwiseClone(); //} } }
(3)贪心算法的实现
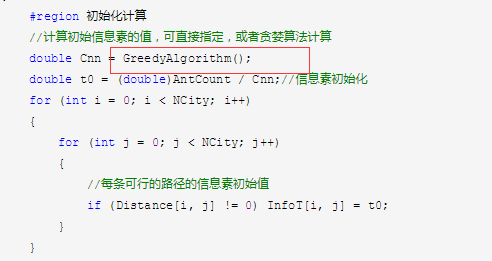
这个原作者也没有给出,于是我自己实现了一下(可能在时间和空间复杂调用上有很大缺陷,这个的优化工作本人暂不处理,大家有兴趣的可以自己实现),代码如下:

private double GreedyAlgorithm() { double sumDistince = 0; //用于存储已经走过的路径,Key为当前出发点,Value为目的地 Dictionary<int, int> edge = new Dictionary<int, int>(); int tempArr1 = 0; int tempArr2 = 0; double min = 0; while (edge.Count < NCity - 1) { #region 初始化起点与下一个到达点,从0开始出发 if (edge.Count < 1) { min = Distance[0, 1]; } else { for (int i = 0; i < NCity; i++) { if (!edge.ContainsKey(i) && Distance[tempArr1, i] != 0) { min = Distance[tempArr1, i]; tempArr2 = i; break; } } } #endregion for (int j = 0; j < NCity; j++) { //搜索当前地到下一目的地的最短距离 if (Distance[tempArr1, j] != 0 && Distance[tempArr1, j] < min && !edge.ContainsKey(j)) { min = Distance[tempArr1, j]; tempArr2 = j; } } if (min == this.Distance[0, 1]) { tempArr2 = 1; } edge.Add(tempArr1, tempArr2); tempArr1 = tempArr2; sumDistince += min; } sumDistince += Distance[tempArr2, 0]; return sumDistince; }
整个群蚁算法的代码基本沿用了原作者的代码,没有什么改变,所以就不贴整套的了。
3、 测试代码:

using BLL.BaiduMap; using Entity.ACO; using Entity.BaiduEntity; using System; using System.Collections.Generic; using System.Linq; using System.Text; namespace OptimalTrack { class Program { static void Main(string[] args) { string[] address = new string[] { "上海市徐汇区", "上海市闵行区", "上海市奉贤区", "上海市普陀区", "上海市静安区", "上海市长宁区" }; double[,] distinces = InitDistinces(address); BaseTspAntSystem tsp = new BaseTspAntSystem(distinces, 10, 1, 2, 0.5, 10); tsp.TspSolution(); foreach (Ant ant in tsp.PlanList) { Console.WriteLine("------------------"); string path = string.Empty; int current = 0; foreach (var item in ant.Edge) { if (current == 0) { path += item.Key + "->" + item.Value + "->"; } else if(current>0&¤t<ant.Edge.Count-1) { path += item.Value + "->"; } else { path += item.Value; } current++; } Console.WriteLine("路径:" + path); Console.WriteLine("------------------"); } } private static double[,] InitDistinces(string[] address) { double[,] distinces = new double[address.Length, address.Length]; MapInfo[] mapInfos = new MapInfo[address.Length]; for (int i = 0; i < address.Length; i++) { mapInfos[i] = BaiduApiHandle.GetLngAndLat(address[i]); } for (int j = 0; j < address.Length; j++) { for (int k = 0; k < address.Length; k++) { if (j == k) { distinces[j, k] = 0; } else { distinces[j, k] = DistinceCalculate.LantitudeLongitudeDist(mapInfos[j].Result.Location.Lng, mapInfos[j].Result.Location.Lat, mapInfos[k].Result.Location.Lng, mapInfos[k].Result.Location.Lat); } } } return distinces; } private static void DisplayAddress() { MapInfo mapInfo = BaiduApiHandle.GetLngAndLat("上海市徐汇区"); Console.WriteLine("状态码:" + mapInfo.Status); Console.WriteLine("经度:" + mapInfo.Result.Location.Lng); Console.WriteLine("纬度:" + mapInfo.Result.Location.Lat); Console.WriteLine("精确度:" + mapInfo.Result.Confidence); } } }
运行结果:

这里注意调整BaseTspAntSystem类构造方法的参数,信息素越强(参数a),即能见度越高,收敛性越强,得到的结果路径就越单一,精确性会差一些,大家可以自己调整下参数观察不同的结果。
4、 总结
这里基本上是在收集别人的代码和成果来解决自己的问题,文章引用的大部分也都是别人的代码,但重点是,一定要自己一点点的理解和尝试。
参考资料:
【1】新浪博客,吴超,根据两点经纬度计算距离【转】;
【2】博客园,数据之巅,群蚁算法理论与实践全攻略——旅行商等路径优化问题的新方法;
【3】网易博客,蚁群优化算法ACO ;
【4】博客园,柠檬雨,Evolutionary Computing: 遗传算法_轮盘赌选择(转载);
【5】博客园,Learning hard, [C#进阶系列]专题一:深入解析深拷贝和浅拷贝;



 浙公网安备 33010602011771号
浙公网安备 33010602011771号