2.5.4 非规则——分形几何

提纲

什么是分形几何？

分数维造型方法

形状语法

分数维造型程序思想：递归

什么是分形几何？

分形，具有非整数维形式充填空间的形态特征。通常被定义为“一个粗糙或零碎的几何形状，可以分成数个部分，且每一部分都（至少近似地）是缩小后的形状”，即具有自相似的性质。

 

与传统集合相比的特点：

1.不规则：从整体上看，分形几何图形是处处不规则的。例如海岸线和山川形状。

2.自相似：在不同尺度上，图形的规则性又是相同的。从近距离观察，其局部形状和整体形态相似，他们从整体到局部，都是自相似的。

又被称为描述大自然的几何学。

 

分形维数的概念：https://www.zhihu.com/question/19931652

 

 

分数维造型方法

分形的定义：

分形几何物体就有一个基本特征：无限的自相似性。

无限的自相似性是指物体的整体和局部之间细节的无线重现。

分数维造型：

分形维数，又称为分数维数

生成过程：初始生成元（initiator）、生成元（generator）

 

 

 

 

 

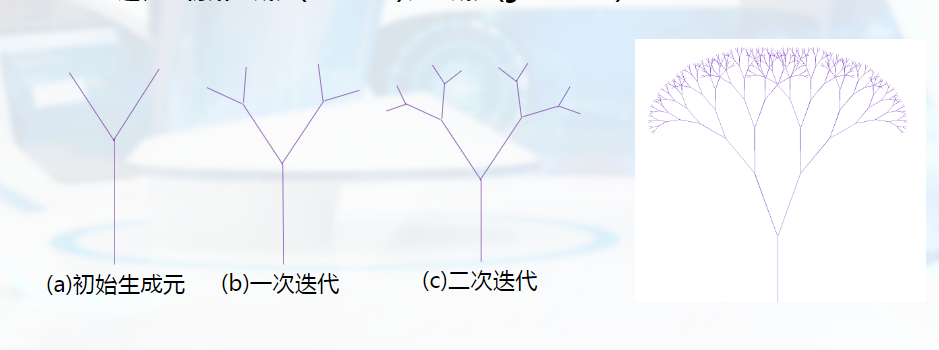
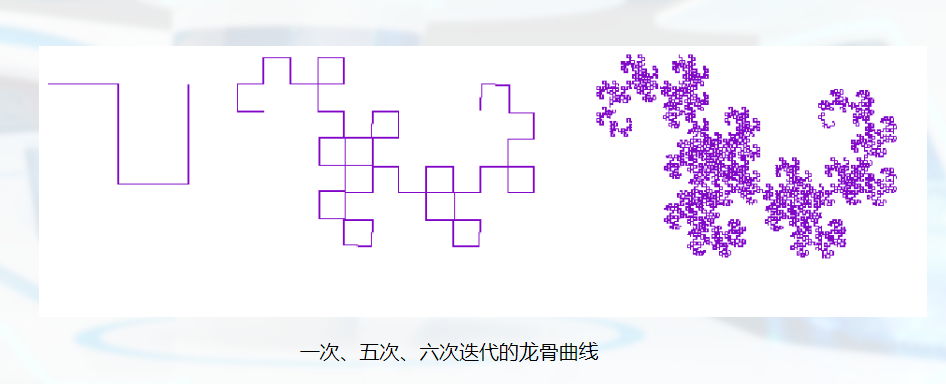
形状语法

形状语法：给定一组产生式规则，形状设计者可以在从给定初始物体到最终物体结构的每一次变换中应用不同的规则。

 

 

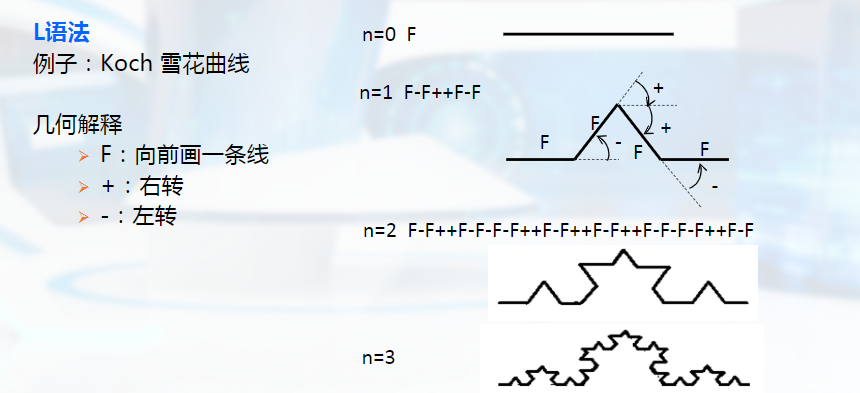
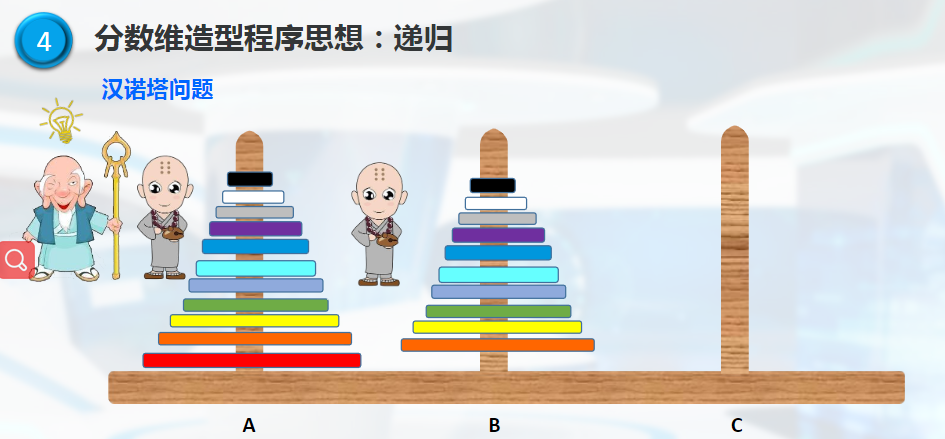
分数维造型程序思想：递归