546. 移除盒子（难） - 8月15日

题目

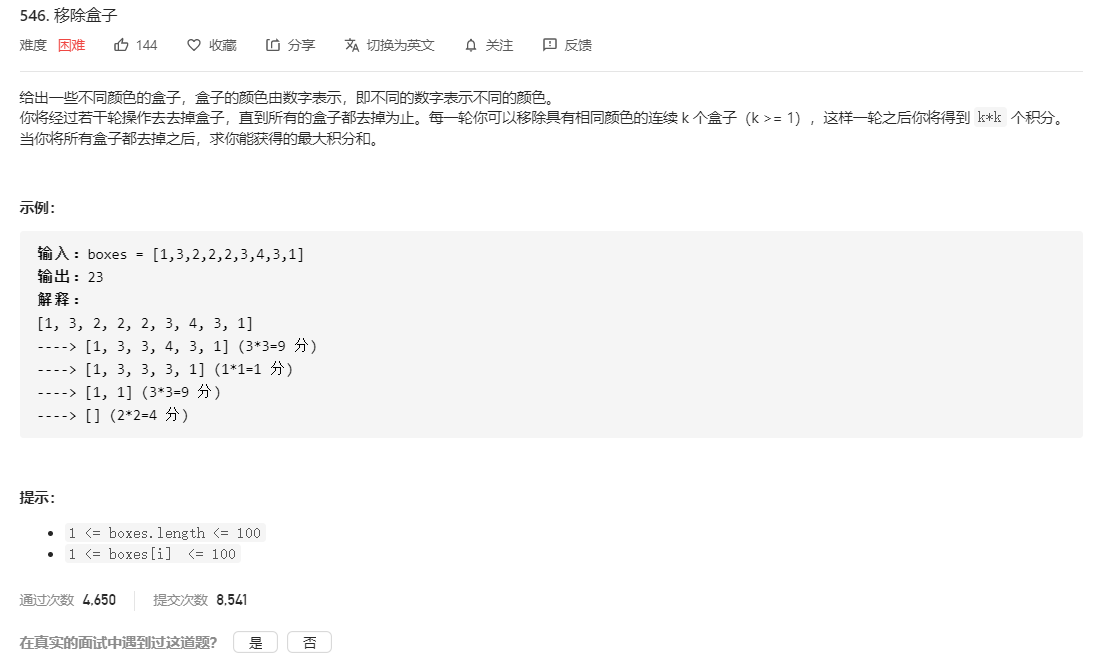
546. 移除盒子

我的思路

一种想法是深搜递归。选择当前盒子中任意一个，删除相同颜色并且连续的盒子后将剩余的盒子继续递归选择并删除。这样直接计算的话复杂度太高了，需要记忆化存储搜索过程来降低复杂度。还没想到合适的。。

另一种想法是动态规划。n个盒子的最大积分和由n-1,n-2,...1个盒子的积分决定：也似乎不方便

还有一种是反向思维，去掉盒子的逆过程是插入盒子？？

参考官方题解，整理一下思路：

设置指针l,r

如果f(l,r)表示l到r区间内的最大积分，那么f(l,r)经过如下递推而得：去除从l位置开始的连续相同元素，假设k个，那么f(l+k-1,r)+k*k;找到第一个与l位置元素相同但不相邻的元素，假设位置在j，那么f(j+1,r)+f(l+k,j-1)+(k+1)^2；再找第二个与l位置元素相同但不相邻的元素，这时需要考虑这个不相邻的元素是否与前面找到的不相邻元素相邻，该元素是直接与l元素块作为邻居去掉还是加上第一个不相邻元素三个一起作为邻居去掉。。。似乎并不便于分析

如果多一个参数f(l,r,k)表示考虑上l左侧有k个与l元素相同的元素，l到r区间内的最大积分。这样可以方便的进行递归分析，f(l,r,k)计算如下：f(l+1,r,0)+(k+1)^2;找到l右侧第p个与l元素相同的位置j，f(jp,r,k+1)+f(l+1,jp-1,0)。以上多个表达式的最大值，可以用三维数组记忆化递归路径。如此递归终止条件是：f(n,n,k) = (k+1)^2;或者f(n,n-1,0) = 0;

我的实现

class Solution {
public:
    vector<vector<vector<int>>> memoryMatrix;
    int dps(int l,int r,int k,vector<int>& boxes){
        if(memoryMatrix[l][r][k]!=0)return memoryMatrix[l][r][k];
        if(l==r){
            //cout<<l<<"\t"<<r<<"\t"<<(k+1)*(k+1)<<endl;
            memoryMatrix[l][r][k] = (k+1)*(k+1);
            return  memoryMatrix[l][r][k];
        }else if(l>r){
            return 0;
        }else{
            if(boxes[l+1]==boxes[l]){
                memoryMatrix[l][r][k] = dps(l+1,r,k+1,boxes); 
                return memoryMatrix[l][r][k];
            }else{
                int j = l+2;
                int tempmax = 0;
                while(j<=r){
                    
                    if(boxes[j]==boxes[l]){
                        //cout<<l<<"=="<<j<<endl;
                        tempmax = max(tempmax,dps(j,r,k+1,boxes)+dps(l+1,j-1,0,boxes));
                    }
                    j++;
                }
                memoryMatrix[l][r][k] =  max(tempmax,dps(l,l,k,boxes)+dps(l+1,r,0,boxes));
                //if(l==1&&r==7)cout<<memoryMatrix[l][r][k]<<"====\n";
                return memoryMatrix[l][r][k];
            }
        }
    }
    int removeBoxes(vector<int>& boxes) {
        int numBoxes = boxes.size();
        for(int i=0;i<=numBoxes;i++){
            vector<vector<int>> temp1;
            
            for(int i=0;i<=numBoxes;i++){
                vector<int> temp2(numBoxes+1,0);
                temp1.push_back(temp2);
            }
            memoryMatrix.push_back(temp1);
        }
        //dps(0,numBoxes-1,0,boxes);
        
        //return 0;
        return dps(0,numBoxes-1,0,boxes);




    }
};
/*
一种想法是深搜递归。选择当前盒子中任意一个，删除相同颜色并且连续的盒子后将剩余的盒子继续递归选择并删除。这样直接计算的话复杂度太高了，需要记忆化存储搜索过程来降低复杂度。还没想到合适的。。

另一种想法是动态规划。n个盒子的最大积分和由n-1,n-2,...1个盒子的积分决定：也似乎不方便

还有一种是反向思维，去掉盒子的逆过程是插入盒子？？


参考官方题解，整理一下思路：

设置指针l,r
如果f(l,r)表示l到r区间内的最大积分，那么f(l,r)经过如下递推而得：去除从l位置开始的连续相同元素，假设k个，那么f(l+k-1,r)+k*k;找到第一个与l位置元素相同但不相邻的元素，假设位置在j，那么f(j+1,r)+f(l+k,j-1)+(k+1)^2；再找第二个与l位置元素相同但不相邻的元素，这时需要考虑这个不相邻的元素是否与前面找到的不相邻元素相邻，该元素是直接与l元素块作为邻居去掉还是加上第一个不相邻元素三个一起作为邻居去掉。。。似乎并不便于分析
如果多一个参数f(l,r,k)表示考虑上l左侧有k个与l元素相同的元素，l到r区间内的最大积分。这样可以方便的进行递归分析，f(l,r,k)计算如下：f(l+1,r,0)+(k+1)^2;找到l右侧第p个与l元素相同的位置j，f(jp,r,k+1)+f(l+1,jp-1,0)。以上多个表达式的最大值，可以用三维数组记忆化递归路径。如此递归终止条件是：f(n,n,k) = (k+1)^2;或者f(n,n-1,0) = 0;

*/

 

拓展学习