读书笔记 -《深入理解计算机系统》2.1
1、进制
计算机作为一种电子计算工具,是由大量的电子器件组成的,在这些电子器件中,电路的通和断、电位的高和低,用两个数字符号“1”和“0”分别表示容易实现。同时二进制的运算法则也很简单,因此,在计算机内部通常用二进制代码来作为内部存储、传输和处理数据。
但是用二进制数表示一个数值时,位数比较长,不便书写和记忆,而用于十进制虽然看起来很方便但是与位模式之间的转换却十分的麻烦。因此,使用十六进制来书写位模式。
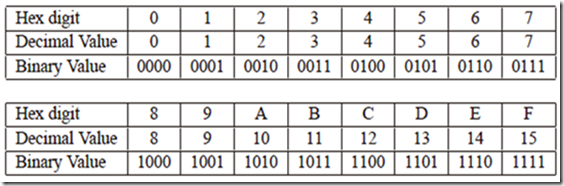
下图为二进制、十进制、十六进制的转换表:
2、单位
字节(byte):用于计量存储容量和传输容量的最小的可存储器单位,1个字节等于8位二进制。
单位的换算:
1字节(Byte)= 8位(bit)
1024字节 = 1KB(2^10字节)
1024KB = 1MB(2^20字节)
1024MB = 1GB(2^30字节)
1GB = 1TB(2^40字节)
3、字长
在同一时间中处理二进制数的位数叫字长。通常称处理字长为8位数据的CPU叫8位CPU,32位CPU就是在同一时间内处理字长为32位的二进制数据。二进制的每一个0或1是组成二进制的最小单位,称为一个比特(bit).
字长:一般说来,计算机在同一时间内处理的一组二进制数称为一个计算机的“字”,而这组二进制数的位数就是“字长”。在其他指标相同时,字长越大计算机的处理数据的速度就越快。早期的微机字长一般是8位和16位,386以及更高的处理器大多是32位。目前市面上的计算机的处理器大部分已达到64位。更多信息查看
4、字节顺序
由来:
我们在写字符流时,因为字符型只占一个字节数,计算机只须按一个字符一个字符写入文件即可。但是如果是处理整型时,由于整型占4个字节,所以一个整型内部的字节存储排列的顺序直接关系到被计算机识别出来的整型值。某种意义上也可直接理解计算机的识别顺序就是所谓的字节顺序。
字节序主要分为:大端法(通常为网络字节序)、小端法(通常为主机字节顺序)
1、小端法(Little-Endian)就是低位字节排放在内存的低地址端即该值的起始地址,高位字节排放在内存的高地址端。
2、大端法(Big-Endian)就是高位字节排放在内存的低地址端即该值的起始地址,低位字节排放在内存的高地址端。
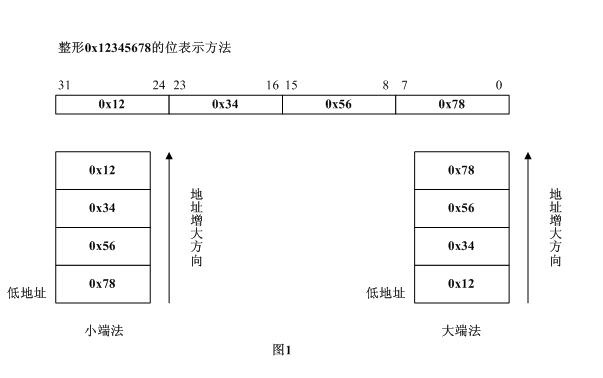
举个简单的例子,对于整形0x12345678。它在大端法和小端法的系统内中,分别如图1所示的方式存放。
5、原码,反码,补码
数值有正负之分,计算机就用一个数的最高位存放符号(0为正,1为负).这就是机器数的原码了.假设机器能处理的位数为8.即字长为1byte,原码能表示数值的范围为(-127~-0 +0~127)共256个.(注:-0将由下面解释)
有了数值的表示方法就可以对数进行算术运算.但是很快就发现用带符号位的原码进行乘除运算时结果正确,而在加减运算的时候就出现了问题,如下: 假设字长为8bits
(1) 10 - (1)10 = (1)10 + (-1)10 = (0)10
(0 0000001)原 + (1 0000001)原 = (1 0000010)原 = ( -2 ) 显然不正确。
因为在两个整数的加法运算中是没有问题的,于是就发现问题出现在带符号位的负数身上。对除符号位外的其余各位逐位取反就产生了反码。反码的取值空间和原码相同且一一对应。下面是反码的减法运算:
(1)10 - (1)10 = (1)10 + (-1)10 = (0)10
(0 0000001)反 + (1 1111110)反 = (1 1111111)反 = ( -0 ) 有问题。
(1)10 - (2)10 = (1)10 + (-2)10 = (-1)10
(0 0000001)反 + (1 1111101)反 = (11111110)反 = (-1) 正确。
问题出现在(+0)和(-0)上,在人们的计算概念中零是没有正负之分的。(印度人首先将零作为标记并放入运算之中,包含有零号的印度数学和十进制计数对人类文明的贡献极大)。
于是就引入了补码概念。负数的补码就是对反码加一,而正数的补码不变,正数的原码反码补码是一样的。在补码中用(-128)代替了(-0),这个是人为规定的,所以补码的表示范围为:
(-128~0~127)共256个。
注意:(-128)没有相对应的原码和反码, (-128) = (1 0000000) 补码的加减运算如下:
(1)10 - (1)10 = (1)10 + (-1)10 = (0)10
(0 0000001)补 + (1 1111111)补 = (0 0000000)补 = ( 0 ) 正确。
(1)10 - (2)10 = (1)10 + (-2)10 = (-1)10
(00000001)补 + (11111110)补 = (11111111)补 = (-1) 正确。
所以补码的设计目的是:
(1)使符号位能与有效值部分一起参加运算,从而简化运算规则。补码机器数中的符号位,并不是强加上去的,是数据本身的自然组成部分,可以正常地参与运算。
(2) 使减法运算转换为加法运算,进一步简化计算机中运算器的线路设计。
所有这些转换都是在计算机的最底层进行的,而在我们使用的汇编、c等其他高级语言中使用的都是原码。