归并排序——思路及其实现
归并排序(MERGE-SORT)是利用归并的思想实现的排序方法,该算法采用经典的分治(divide-and-conquer)策略(分治法将问题分(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起,即分而治之)。
归并排序中,我们会先找到一个数组的中间下标mid,然后以这个mid为中心,对两边分别进行排序,之后我们再根据两边已排好序的子数组,重新进行值大小分配。
我们就以下面的数组为例:
![]()
(1)mid等于数组最大下标 / 2 = 3,于是我们以下标3(值为7)为中心,分别排序0~3和4~7的数字。
(2)此时两边的数组还可以创建分支:

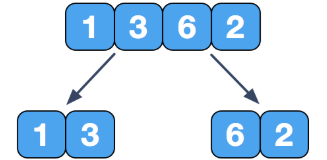
(3)可以看到上面还有四个小数组,我们继续创建分支:
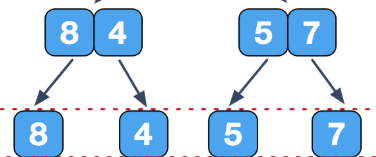
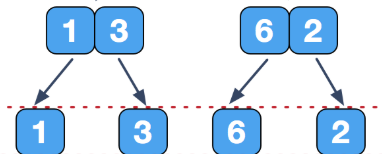
(4)可以看到,此时我们已经无法继续创建分支了,因为数组数量为1时是没有必要进行排序的,这时我们可以开始进行对每一个小的数组进行排序并且合并:
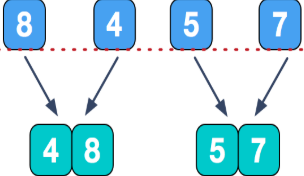
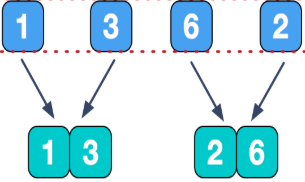
(5)继续,拿到上一步组成的小数组,再组合成新的排序数组:
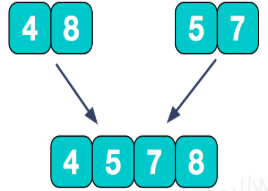
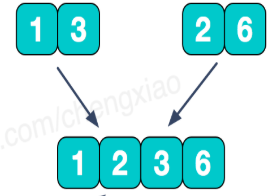
(6)最后,我们想要的结果就来了:
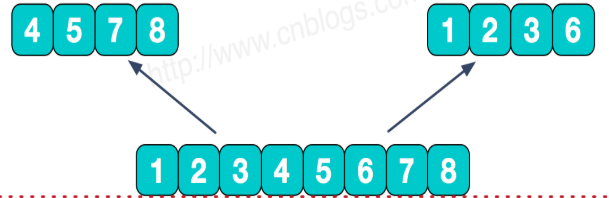
代码如下:
public class MergeSort {
public static void mergeSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
mergeSort(arr, 0, arr.length - 1);
}
public static void mergeSort(int[] arr, int l, int r) {
if (l == r) {
return;
}
int mid = l + ((r - l) >> 1);
mergeSort(arr, l, mid);
mergeSort(arr, mid + 1, r);
merge(arr, l, mid, r);
}
public static void merge(int[] arr, int l, int m, int r) {
int[] help = new int[r - l + 1];
int i = 0;
int l1 = l;
int r1 = m + 1;
while (l1 <= m && r1 <= r) {
help[i++] = arr[l1] < arr[r1] ? arr[l1++] : arr[r1++];
}
while (l1 <= m) {
help[i++] = arr[l1++];
}
while (r1 <= r) {
help[i++] = arr[r1++];
}
for (int j = 0; j < help.length; j++) {
arr[l + j] = help[j];
}
}
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号