图的迪杰斯特拉算法求最短路径

转载：http://www.cnblogs.com/skywang12345/

迪杰斯特拉算法介绍

迪杰斯特拉(Dijkstra)算法是典型最短路径算法，用于计算一个节点到其他节点的最短路径。 
它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想)，直到扩展到终点为止。

基本思想

     通过Dijkstra计算图G中的最短路径时，需要指定起点s(即从顶点s开始计算)。

     此外，引进两个集合S和U。S的作用是记录已求出最短路径的顶点(以及相应的最短路径长度)，而U则是记录还未求出最短路径的顶点(以及该顶点到起点s的距离)。

     初始时，S中只有起点s；U中是除s之外的顶点，并且U中顶点的路径是"起点s到该顶点的路径"。然后，从U中找出路径最短的顶点，并将其加入到S中；接着，更新U中的顶点和顶点对应的路径。 然后，再从U中找出路径最短的顶点，并将其加入到S中；接着，更新U中的顶点和顶点对应的路径。 ... 重复该操作，直到遍历完所有顶点。

操作步骤

(1) 初始时，S只包含起点s；U包含除s外的其他顶点，且U中顶点的距离为"起点s到该顶点的距离"[例如，U中顶点v的距离为(s,v)的长度，然后s和v不相邻，则v的距离为∞]。

(2) 从U中选出"距离最短的顶点k"，并将顶点k加入到S中；同时，从U中移除顶点k。

(3) 更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离，是由于上一步中确定了k是求出最短路径的顶点，从而可以利用k来更新其它顶点的距离；例如，(s,v)的距离可能大于(s,k)+(k,v)的距离。

(4) 重复步骤(2)和(3)，直到遍历完所有顶点。

单纯的看上面的理论可能比较难以理解，下面通过实例来对该算法进行说明。

迪杰斯特拉算法图解

 

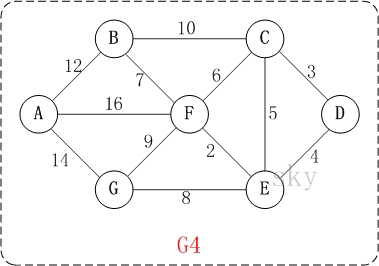
以上图G4为例，来对迪杰斯特拉进行算法演示(以第4个顶点D为起点)。

 

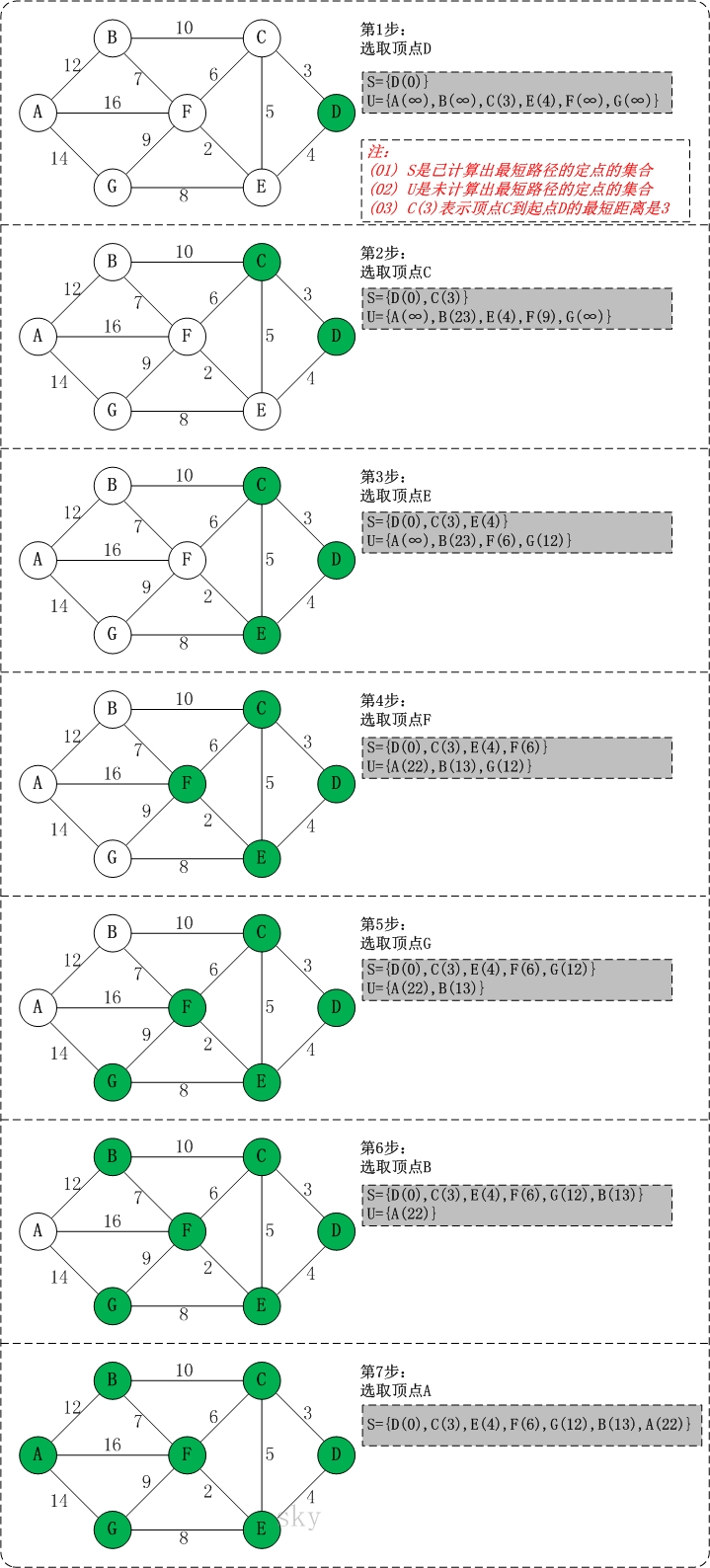
初始状态：S是已计算出最短路径的顶点集合，U是未计算除最短路径的顶点的集合！ 
第1步：将顶点D加入到S中。 
    此时，S={D(0)}, U={A(∞),B(∞),C(3),E(4),F(∞),G(∞)}。     注:C(3)表示C到起点D的距离是3。

第2步：将顶点C加入到S中。 
    上一步操作之后，U中顶点C到起点D的距离最短；因此，将C加入到S中，同时更新U中顶点的距离。以顶点F为例，之前F到D的距离为∞；但是将C加入到S之后，F到D的距离为9=(F,C)+(C,D)。 
    此时，S={D(0),C(3)}, U={A(∞),B(23),E(4),F(9),G(∞)}。

第3步：将顶点E加入到S中。 
    上一步操作之后，U中顶点E到起点D的距离最短；因此，将E加入到S中，同时更新U中顶点的距离。还是以顶点F为例，之前F到D的距离为9；但是将E加入到S之后，F到D的距离为6=(F,E)+(E,D)。 
    此时，S={D(0),C(3),E(4)}, U={A(∞),B(23),F(6),G(12)}。

第4步：将顶点F加入到S中。 
    此时，S={D(0),C(3),E(4),F(6)}, U={A(22),B(13),G(12)}。

第5步：将顶点G加入到S中。 
    此时，S={D(0),C(3),E(4),F(6),G(12)}, U={A(22),B(13)}。

第6步：将顶点B加入到S中。 
    此时，S={D(0),C(3),E(4),F(6),G(12),B(13)}, U={A(22)}。

第7步：将顶点A加入到S中。 
    此时，S={D(0),C(3),E(4),F(6),G(12),B(13),A(22)}。

此时，起点D到各个顶点的最短距离就计算出来了：A(22) B(13) C(3) D(0) E(4) F(6) G(12)。

代码实现如下，以邻接矩阵实现的：

public class DnjavaDijstra {
	private final static int MAXVEX = 4;
	private final static int MAXWEIGHT = 65535;
	private int shortTablePath[] = new int[MAXVEX];// 记录的是v0到某顶点的最短路径和

	/**
	 * 获取一个图的最短路径
	 */
	public void shortestPathDijstra(Graph graph) {
		int min;
		int k = 0;// 记录下标
		boolean isgetPath[] = new boolean[MAXVEX];
		for (int v = 0; v < graph.getVertexSize(); v++) {
			shortTablePath[v] = graph.getMatrix()[0][v];// 获取v0这一行的权值数组
		}
		shortTablePath[0] = 0;
		isgetPath[0] = true;
		for (int v = 1; v < graph.getVertexSize(); v++) {
			min = MAXWEIGHT;
			// 找到最短权值数组里的最小值（前提是没有被确定过得）
			for (int i = 1; i < graph.getVertexSize(); i++) {
				if (!isgetPath[i] && shortTablePath[i] < min) {
					min = shortTablePath[i];
					k = i;
				}
			}
			// 出来后，当前的k是选出的最小值的下标，把该下标设置为确定的
			isgetPath[k] = true;
			for (int i = 1; i < graph.getVertexSize(); i++) {
				if (!isgetPath[i]
						&& ((min + graph.getMatrix()[k][i]) < shortTablePath[i])) {
					// 如果小于的话，就替换
					shortTablePath[i] = min + graph.getMatrix()[k][i];
				}
			}
		}

		for (int i = 0; i < graph.getVertexSize(); i++) {
			System.out.println("  " + i + "  最短路径" + shortTablePath[i] + "\n");
		}
	}
}