图的克鲁斯卡尔算法求最小生成树
克鲁斯卡尔算法的核心思想是:在带权连通图中,不断地在边集合中找到最小的边,如果该边满足得到最小生成树的条件,就将其构造,直到最后得到一颗最小生成树。
克鲁斯卡尔算法的执行步骤:
第一步:在带权连通图中,将边的权值排序(从小到大);
第二步:判断是否需要选择这条边(此时图中的边已按权值从小到大排好序)。判断的依据是边的两个顶点是否已连通,如果连通则继续下一条;如果不连通,那么就选择使其连通。
第三步:循环第二步,直到图中所有的顶点都在同一个连通分量中,即得到最小生成树。
下面我用图示法来演示克鲁斯卡尔算法的工作流程,如下图:
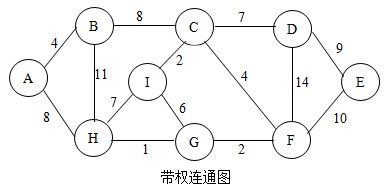
首先,将图中所有的边排序(从小到大),我们将以此结果来选择。排序后各边按权值从小到大依次是:
HG < (CI=GF) < (AB=CF) < GI < (CD=HI) < (AH=BC) < DE < BH < DF
并且定义一个parent[]数组,大小为图中顶点个数,初始化{0,0,0,0,0,0,0,0,0},下标对应的值是当前顶点的终结点。
H到G:1、C到I:2、G到F:2、A到B:4、C到F:4、G到I:6、C到D:7、H到I:7、A到H:8、B到C:8、D到E:9、B到H:11、D到F:14
需要注意的是:我们把上面左边左边定位begin,右边顶点定为end,例如HG:H begin G end
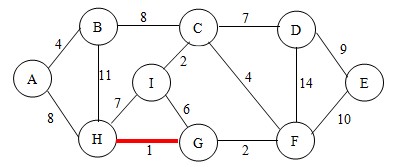
判断法则:当将边CI加入到已找到边的集合中时,是否会形成回路?
1.我们首先要判断C和I这俩顶点分别的终顶点,C(parent对应的2下标),I(对应8下标),都是0,所以没有回环,可以连
2.如果C和I俩终顶点是一样的,形成回路,不符合要求,直接进行下一次操作

继续,选择GF边,对G和F分别判断终顶点是谁,因为parent数组下标5和6都是0,所以没有回环,可以连

parent={0,0,8,0,0,0,5,6,0},意思是G顶点的终顶点是5下标(F)了
继续,选择AB进行判断,因为parent数组下标0,1都是0,所以不回环,可以连接
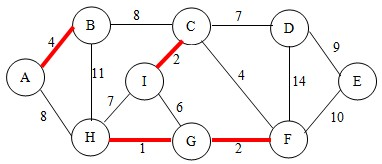
parent={1,0,8,0,0,0,5,6,0},意思是G顶点的终顶点是5下标(F)了
继续,对CF进行判断,注意了parent数组下标是2对应的值是8(I),但是8下标对应的值是0,也就是说目前C的终顶点是I,F对应的下标5对应的值是0,所以他俩终点不一样,可以连接!
同时,把I的终顶点设为F
parent={1,0,8,0,0,0,5,6,5},意思是I顶点的终顶点是5下标(F)了
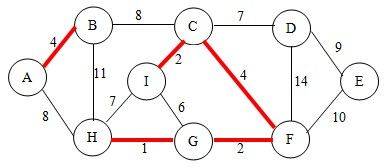
继续,这次选择GI,注意了parent数组下标6对应的值是5,8下标的值是5,所以形成了回环,不可连!
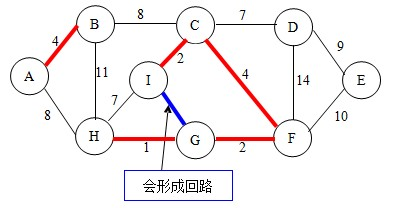
继续,选择CD,C和D对应的终顶点是F和无,所以CD可以连!同时把C的终顶点F的终顶点设为D
parent={1,0,8,0,0,3,5,6,5},意思是F顶点的终顶点是3下标(D)了
继续对边集合所有的边按照上面的规则判断,得到最终的最小生成树是:
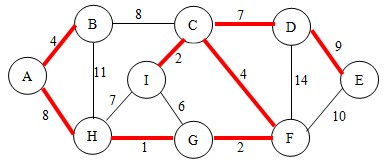
代码如下:
public class GraphKruskal2 {
public Edge[] edges;
public int edgeSize;;
public GraphKruskal2(int edgeSize) {
this.edgeSize = edgeSize;
edges = new Edge[edgeSize];
}
public void createEdgeArray() {
Edge edge0 = new Edge(4, 7, 7);
Edge edge1 = new Edge(2, 8, 8);
Edge edge2 = new Edge(0, 1, 10);
Edge edge3 = new Edge(0, 5, 11);
Edge edge4 = new Edge(1, 8, 12);
Edge edge5 = new Edge(3, 7, 16);
Edge edge6 = new Edge(1, 6, 16);
Edge edge7 = new Edge(5, 6, 17);
Edge edge8 = new Edge(1, 2, 18);
Edge edge9 = new Edge(6, 7, 19);
Edge edge10 = new Edge(3, 4, 20);
Edge edge11 = new Edge(3, 8, 21);
Edge edge12 = new Edge(2, 3, 22);
Edge edge13 = new Edge(3, 6, 24);
Edge edge14 = new Edge(4, 5, 26);
edges[0] = edge0;
edges[1] = edge1;
edges[2] = edge2;
edges[3] = edge3;
edges[4] = edge4;
edges[5] = edge5;
edges[6] = edge6;
edges[7] = edge7;
edges[8] = edge8;
edges[9] = edge9;
edges[10] = edge10;
edges[11] = edge11;
edges[12] = edge12;
edges[13] = edge13;
edges[14] = edge14;
}
class Edge {
public int begin;
public int end;
public int weight;
public Edge(int begin, int end, int weight) {
this.begin = begin;
this.end = end;
this.weight = weight;
}
}
public void kruskal() {
int m, n, sum = 0;
int[] parent = new int[edgeSize];// 下标指顶点位置,值指的是当前下标对应的顶点邻接父节点
for (int i = 0; i < edgeSize; i++) {
parent[i] = 0;
}
for (int i = 0; i < edgeSize; i++) {
// 对边数组进行从小到大遍历
// 找到边的begin,判断当前begin的终顶点
n = find(parent, edges[i].begin);
// 找到边的end,判断当前end的终顶点
m = find(parent, edges[i].end);
// 如果当前n=m的话,就代表有回环,不能连接
if (n != m) {
parent[n] = m;
System.out.println("起始顶点:" + edges[i].begin + " ---结束顶点:"
+ edges[i].end);
sum += edges[i].weight;
} else {
System.out.println("第" + i + "条边回环了");
}
}
System.out.println("权值总和:" + sum);
printArray(parent);
}
private int find(int[] parent, int f) {
// 找到当前f节点的父节点的父节点.....(以此类推)的下标
while (parent[f] > 0) {
System.out.println("找到起点:" + f);
f = parent[f];
System.out.println("找到终点:" + f);
}
return f;// 返回的这个代表当前f暂时还没有了父节点
}
// (3)
public static void printArray(int[] array) {
System.out.print("{");
for (int i = 0; i < array.length; i++) {
System.out.print(array[i]);
if (i < array.length - 1) {
System.out.print(", ");
}
}
System.out.println("}");
}
public static void main(String[] args) {
GraphKruskal2 kruskal = new GraphKruskal2(15);
kruskal.createEdgeArray();
kruskal.kruskal();
}
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号