图的普里姆(Prim)算法求最小生成树
关于图的最小生成树算法------普里姆算法
首先我们先初始化一张图:

设置两个数据结构来分别代表我们需要存储的数据:
lowcost[i]:表示以i为终点的边的最小权值,当lowcost[i]=0说明以i为终点的边的最小权值=0,也就是表示i点加入了mst数组
mst[i]:这个数组对应的下标(图顶点)的值,是当前最小生成树表示的顶点的连接的那个边的权值
我们假设v1是初始点,进行初始化,不相连的用*表示,表示无穷大!
我们先把所有v1对应的顶点的权值放进lowcost数组中,进行初始化,之后我们取出lowcost中最小的权值:
lowcost[2]=6,lowcost[3]=1,lowcost[4]=5,lowcost[5]=*,lowcost[6]=*
mst[2]=1,mst[3]=1,mst[4]=1,mst[5]=1,mst[6]=1,(所有点默认起点是V1)
明显看出,以V3为终点的边的权值最小=1,所以这条边加入mst,注意,找到最小值时(1这个值在lowcost里对应的是下标2,顶点v3),说明当前v3已经确定了他所选择的最小权值边(以v3为主动连接方),记得把lowcost[3]设置为0,代表已经确定的!!
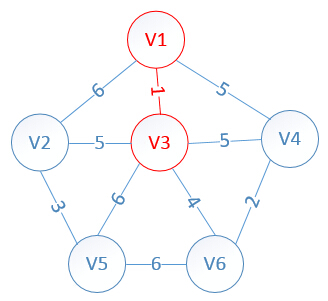
此时,因为点V3的加入,需要更新lowcost数组和mst数组,为什么要这么更新?因为当从v1里面选出v3的时候,这个时候我们就从v3开始继续规划,因为v3的对应权值数组是:
v3:{1,5,0,5,6,4}
而此时lowcost数组值是:{1,6,0,5,*,*}
这时我们拿lowcost数组和v3对应的权值数组比较(下标要对应),把v3里比low里小的值替换给low数组(这么做的意义是,例如,下标为1时,v3是5,low是6,也就是说,下标为1对应的顶点是v2,v2可以选择和v3连接(因为权值5<6),所以5会替换6),这样得到的最终lowcost为:
lowcost[2]=5,lowcost[3]=0,lowcost[4]=5,lowcost[5]=6,lowcost[6]=4
mst[2]=3,mst[3]=0,mst[4]=1,mst[5]=3,mst[6]=3
明显看出,以V6为终点的边的权值最小=4,所以边<mst[6],6>=4加入MST

此时,因为点V6的加入,需要更新lowcost数组和mst数组,为什么要这么更新?因为当从v3里面选出v6的时候,这个时候我们就从v6开始继续规划,因为v6的对应权值数组是:
v6:{*,*,4,2,6,0}
而此时lowcost数组值是:{1,5,0,5,6,0}
这时我们拿lowcost数组和v6对应的权值数组比较(下标要对应),把v6里比low里小的值替换给low数组(这么做的意义是,例如,下标为3时,v6是2,low是5,也就是说,下标为3对应的顶点是v4,v4可以选择和v6连接(因为权值2<5),所以5会替换2),这样得到的最终lowcost为:
lowcost[2]=5,lowcost[3]=0,lowcost[4]=2,lowcost[5]=6,lowcost[6]=0
mst[2]=3,mst[3]=0,mst[4]=6,mst[5]=3,mst[6]=0
明显看出,以V4为终点的边的权值最小=2,所以边<mst[4],4>=4加入MST
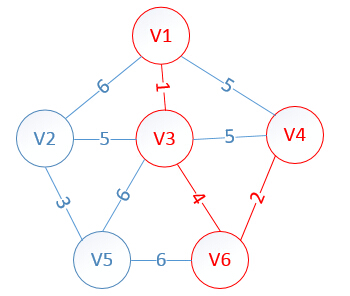
此时,因为点V4的加入,需要更新lowcost数组和mst数组,为什么要这么更新?因为当从v6里面选出v4的时候,这个时候我们就从v4开始继续规划,因为v4的对应权值数组是:
v4:{5,*,5,0,*,2}
而此时lowcost数组值是:{1,5,0,0,6,0}
这时我们拿lowcost数组和v4对应的权值数组比较(下标要对应),把v4里比low里小的值替换给low数组,但是可惜的是,没有找到v4里要比lowcost小的(0不算)这样得到的最终lowcost为:
lowcost[2]=5,lowcost[3]=0,lowcost[4]=0,lowcost[5]=6,lowcost[6]=0
mst[2]=3,mst[3]=0,mst[4]=0,mst[5]=3,mst[6]=0
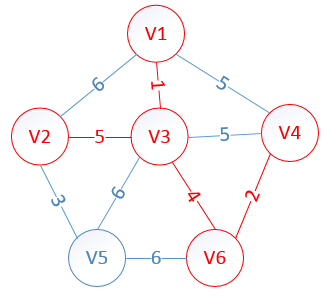
明显看出,以V2为终点的边的权值最小=5,所以边<mst[2],2>=5加入MST
此时,因为点V2的加入,需要更新lowcost数组和mst数组,为什么要这么更新?因为当从v4里面选出v2的时候,这个时候我们就从v2开始继续规划,因为v2的对应权值数组是:
v2:{6,0,5,*,3,*}
而此时lowcost数组值是:{1,0,0,0,6,0}
这时我们拿lowcost数组和v2对应的权值数组比较(下标要对应),把v2里比low里小的值替换给low数组,找到v2里要比lowcost小的(0不算)这样得到的最终lowcost为:
lowcost[2]=0,lowcost[3]=0,lowcost[4]=0,lowcost[5]=3,lowcost[6]=0
mst[2]=0,mst[3]=0,mst[4]=0,mst[5]=2,mst[6]=0
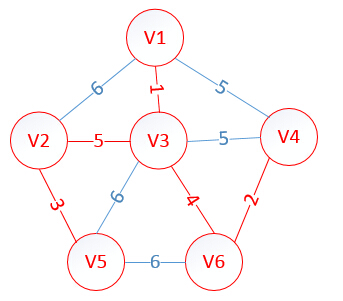
很明显,以V5为终点的边的权值最小=3,所以边<mst[5],5>=3加入MST
lowcost[2]=0,lowcost[3]=0,lowcost[4]=0,lowcost[5]=0,lowcost[6]=0
mst[2]=0,mst[3]=0,mst[4]=0,mst[5]=0,mst[6]=0
至此,MST构建成功,如图所示:
代码如下(仅供参考!):




 浙公网安备 33010602011771号
浙公网安备 33010602011771号