有向图的拓补排序算法

拓扑排序算法介绍

拓扑排序解决的是一系列相互依赖的事件的排序问题，比如Ant中有很多的Task，而某些Task依赖于另外的Task，编译之前需要清理空间，打包之前要先编译，但其它一些Task处理顺序可以调换(是无所谓前后，不是并行), 如何安排Task的执行顺序就可以用拓扑排序解决。熟悉Java的朋友应该都知道Spring，一个非常优秀的解决组件(Bean)依赖的框架，组件之间可能有依赖关系，也可能没有关系，如何按顺序创建组件也是相同的问题。本文使用的是图搜索算法里面的深度优先排序算法解决问题。需要特别指出的是拓扑排序算法的结果很可能有多个(不依赖的可以调换位置)，而算法也可以有多种，深度优先排序算法只是其中一种而已。拓扑排序为线性排序，效率为O(|V|+|E|)，其中|V|表示顶点数，|E|表示边的数量。

 

Java实现有向图的拓补排序：

思路：关于有向图的拓补排序：

   首先我们要确定好一个规则，就是一个顶点他的那些入度对应的顶点全部用完，才可以轮到该顶点自己！

如图：

 

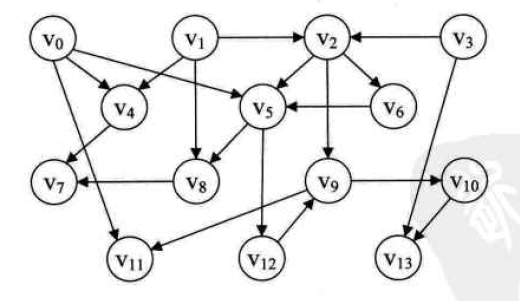
例如v2，他有俩入度，那么要想使用v2，就必须等待v1和v3执行完！

首先我们建立一个栈Stack，把v0，v1，v3压栈；

然后拿出v3，打印v3，看看v3有哪些出度对应的顶点（这里是v2和v13），看看这俩顶点除了v3这个入度外还有没有其他的入度，有的话不能压栈。。

以此类推。。。

 

代码实现如下：

public class DnGraphTopologic {
	private int numVertexes;
	private VertexNode[] adjList;// 邻接顶点的一维数组

	public DnGraphTopologic(int numVertexes) {
		this.numVertexes = numVertexes;
	}

	private void createGraph() {
		VertexNode node0 = new VertexNode(0, "v0");
		VertexNode node1 = new VertexNode(0, "v1");
		VertexNode node2 = new VertexNode(2, "v2");
		VertexNode node3 = new VertexNode(0, "v3");
		VertexNode node4 = new VertexNode(2, "v4");
		VertexNode node5 = new VertexNode(3, "v5");
		VertexNode node6 = new VertexNode(1, "v6");
		VertexNode node7 = new VertexNode(2, "v7");
		VertexNode node8 = new VertexNode(2, "v8");
		VertexNode node9 = new VertexNode(1, "v9");
		VertexNode node10 = new VertexNode(1, "v10");
		VertexNode node11 = new VertexNode(2, "v11");
		VertexNode node12 = new VertexNode(1, "v12");
		VertexNode node13 = new VertexNode(2, "v13");
		adjList = new VertexNode[numVertexes];
		adjList[0] = node0;
		adjList[1] = node1;
		adjList[2] = node2;
		adjList[3] = node3;
		adjList[4] = node4;
		adjList[5] = node5;
		adjList[6] = node6;
		adjList[7] = node7;
		adjList[8] = node8;
		adjList[9] = node9;
		adjList[10] = node10;
		adjList[11] = node11;
		adjList[12] = node12;
		adjList[13] = node13;
		node0.firstEdge = new EdgeNode(11);
		node0.firstEdge.next = new EdgeNode(5);
		node0.firstEdge.next.next = new EdgeNode(4);
		node1.firstEdge = new EdgeNode(8);
		node1.firstEdge.next = new EdgeNode(4);
		node1.firstEdge.next.next = new EdgeNode(2);
		node2.firstEdge = new EdgeNode(9);
		node2.firstEdge.next = new EdgeNode(6);
		node2.firstEdge.next.next = new EdgeNode(5);
		node3.firstEdge = new EdgeNode(13);
		node3.firstEdge.next = new EdgeNode(2);
		node4.firstEdge = new EdgeNode(7);
		node5.firstEdge = new EdgeNode(12);
		node5.firstEdge.next = new EdgeNode(8);
		node6.firstEdge = new EdgeNode(5);
		node8.firstEdge = new EdgeNode(7);
		node9.firstEdge = new EdgeNode(11);
		node9.firstEdge.next = new EdgeNode(10);
		node10.firstEdge = new EdgeNode(13);
		node12.firstEdge = new EdgeNode(9);
		EdgeNode n11 = new EdgeNode(11);
		EdgeNode n5 = new EdgeNode(5);
		EdgeNode n4 = new EdgeNode(4);
		EdgeNode n8 = new EdgeNode(8);
		EdgeNode n2 = new EdgeNode(2);
		EdgeNode n9 = new EdgeNode(9);
		EdgeNode n6 = new EdgeNode(6);
		EdgeNode n13 = new EdgeNode(13);
		EdgeNode n7 = new EdgeNode(7);
		EdgeNode n12 = new EdgeNode(12);
		EdgeNode n10 = new EdgeNode(10);
		/*
		 * 为啥下面不可以同一个n5多个共用？因为公用的话，会出现上面n5还有next，到了下面n5明明不应该有，但是也还是有了,
		 * 当时我还想，如果不是同一个对象的话,那出度会不会受影响，但是我想多了，因为出度不是由n5决定的，
		 * 而是由adjlist来决定的，这个倒是只创建了一个对象。
		 */
		// node0.firstEdge = n11;
		// node0.firstEdge.next = n5;
		// node0.firstEdge.next.next = n4;
		// node1.firstEdge = n8;
		// node1.firstEdge.next = n4;
		// node1.firstEdge.next.next = n2;
		// node2.firstEdge = n9;
		// node2.firstEdge.next = n6;
		// node2.firstEdge.next.next = n5;
		// node3.firstEdge = n13;
		// node3.firstEdge.next = n2;
		// node4.firstEdge = n7;
		// node5.firstEdge = n12;
		// node5.firstEdge.next = n8;
		// node6.firstEdge = n5;
		// node8.firstEdge = n7;
		// node9.firstEdge = n11;
		// node9.firstEdge.next = n10;
		// node10.firstEdge = n13;
		// node12.firstEdge = n9;
	}

	/**
	 * 拓扑排序
	 * 
	 * @author Administrator
	 * @throws Exception
	 * 
	 */
	private void topologicalSort() throws Exception {
		Stack<Integer> stack = new Stack<>();
		int count = 0;
		int k = 0;
		// 开头就先把入度为0的vertexNode压栈（如果没有，就代表有回环）
		for (int i = 0; i < numVertexes; i++) {
			if (adjList[i].in == 0) {
				stack.push(i);
			}
		}
		while (stack.size() > 0) {
			// 取出栈中的下标值
			int pop = stack.pop();
			System.out.println("访问到：" + adjList[pop].data);
			count++;
			// 判断该顶点的其他出度对应的顶点是否无入度了，没有的话打印
			for (EdgeNode node = adjList[pop].firstEdge; node != null; node = node.next) {
				if (--adjList[node.getAdjVert()].in == 0) {
					// 证明该顶点没有了入度，可以压栈
					stack.push(node.getAdjVert());
				}
			}
		}
		if (count < numVertexes) {
			throw new Exception("完犊子了，拓扑排序失败");
		}
	}

	// 边表顶点
	class EdgeNode {
		private int adjVert;
		private EdgeNode next;
		private int weight;

		public EdgeNode(int adjVert) {
			this.adjVert = adjVert;
		}

		public int getAdjVert() {
			return adjVert;
		}

		public void setAdjVert(int adjVert) {
			this.adjVert = adjVert;
		}

		public EdgeNode getNext() {
			return next;
		}

		public void setNext(EdgeNode next) {
			this.next = next;
		}

		public int getWeight() {
			return weight;
		}

		public void setWeight(int weight) {
			this.weight = weight;
		}

	}

	// 邻接顶点
	class VertexNode {
		private int in;// 入度
		private String data;
		private EdgeNode firstEdge;

		public VertexNode(int in, String data) {
			this.in = in;
			this.data = data;
		}

		public int getIn() {
			return in;
		}

		public void setIn(int in) {
			this.in = in;
		}

		public String getData() {
			return data;
		}

		public void setData(String data) {
			this.data = data;
		}

		public EdgeNode getFirstEdge() {
			return firstEdge;
		}

		public void setFirstEdge(EdgeNode firstEdge) {
			this.firstEdge = firstEdge;
		}

	}

	public static void main(String[] args) {
		DnGraphTopologic dnGraphTopologic = new DnGraphTopologic(14);
		dnGraphTopologic.createGraph();
		try {
			dnGraphTopologic.topologicalSort();
		} catch (Exception e) {
			e.printStackTrace();
		}
	}
}