【POJ】[1328]Radar Installation
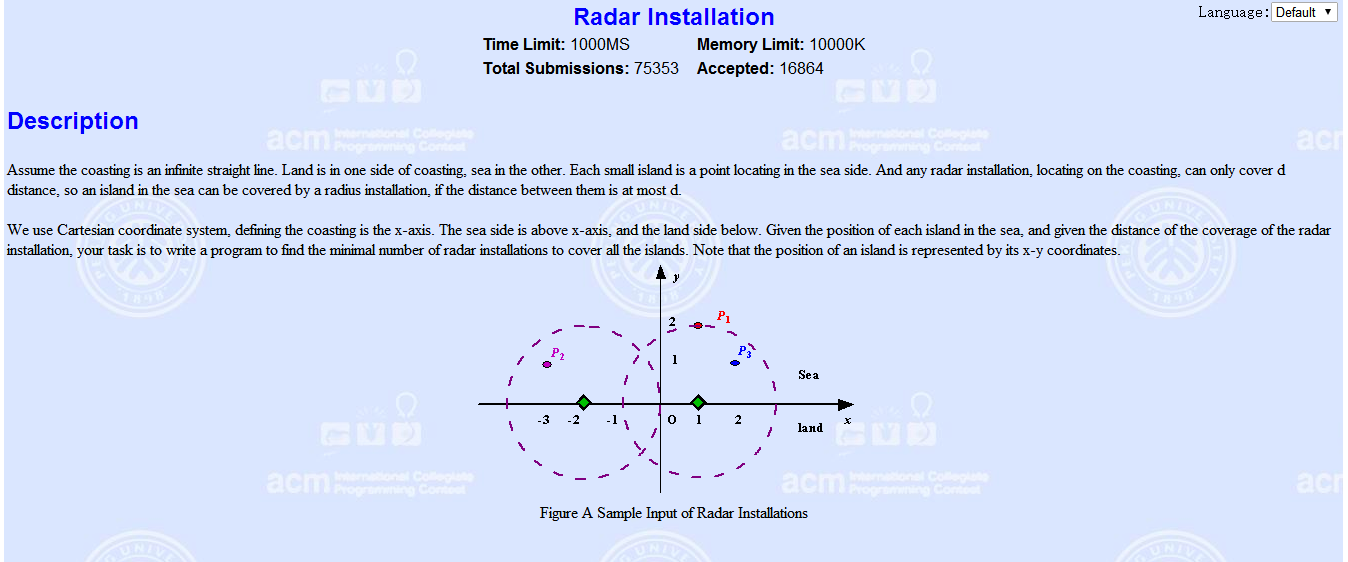
因为雷达必须要建立在x轴上
所以当y>d则-1
求出以点为圆心，d为半径的圆
与x轴交于两点
若雷达在两点之间
则可以覆盖这个点
因为区间有重合的部分
所以只需在重合部分放点
则可以覆盖尽量多的点
由此可把问题转换为
给出数段区间
问使每个区间至少有一个点需要多少点
所以想出贪心策略
可以区间右端点排序
比较时假设在第一个右端点建立雷达
坐标记为t
则若下一端点的左端点在此点之后
则把t更新为下一端点的右端点
并使cnt++
#include<stdio.h>
#include<math.h>
#include<algorithm>
using namespace std;
struct node {
double x,y;
double l,r;
} a[1200];
bool cmp(node A,node B) {
if(A.r==B.r)
return A.l>B.l;
else
return A.r<B.r;
}
int main() {
int n,kase=0;
double d;
while(scanf("%d %lf",&n,&d),n||d) {
bool flag=false;
for(int i=0; i<n; i++) {
scanf("%lf %lf",&a[i].x,&a[i].y);
if(a[i].y>d)
flag=true;
}
printf("Case %d: ",++kase);
if(flag) {
printf("-1\n");
continue;
}
for(int i=0; i<n; i++) {
a[i].r=a[i].x+sqrt(d*d-a[i].y*a[i].y);
a[i].l=a[i].x-sqrt(d*d-a[i].y*a[i].y);
}
sort(a,a+n,cmp);
int cnt=1;
double t=a[0].r;
for(int i=1; i<n; i++) {
if(a[i].l>t) {
cnt++;
t=a[i].r;
}
}
printf("%d\n",cnt);
}
return 0;
}
