\(\;\;\;\;\;\)估计,顾名思义就是对变量的估计咯,我们在对变量进行预测时,希望估计值能尽可能地逼近真实值。为了区分真实值和估计值,我们习惯用\(\theta\)表示真实值,用\(\hat \theta\)表示估计值。令\({\rm{\{ }}{x^{(1)}} \cdots {x^{(m)}}{\rm{\} }}\)是\(m\)个独立同分布的数据点。点估计是这些数据的任意函数:\({\hat \theta _m} = g({x^{(1)}} \cdots {x^{(m)}})\),理想的估计值\(\hat \theta\)将尽可能的接近真实参数\(\theta\)。偏差则用来定义估计值的期望与真实值之间的差距:\(bias({\hat \theta _m}) = E({\hat \theta _m}) - \theta\)。
\(\;\;\;\;\;\)现考虑一组独立同分布的样本\({\rm{\{ }}{x^{(1)}} \cdots {x^{(m)}}{\rm{\} }}\)服从高斯分布\(p({x^{(i)}}) = N({x^{(i)}};\mu ,{\sigma ^2})\),其中\(i \in \{ 1, \cdots ,m\}\)。高斯均值的估计即样本均值:\({\hat \mu _m} = \frac{1}{m}\sum\limits_{i = 1}^m {{x^{(i)}}}\),判断样本均值是否为无偏估计,我们可通过计算偏差来确认:
\[\begin{array}{l}
bias({{\hat \theta }_m}) = E({{\hat \mu }_m}) - \mu \\
\;\;\;\;\;\;\;\;\;\;\;\;\; = E(\frac{1}{m}\sum\limits_{i = 1}^m {{x^{(i)}}} ) - \mu \\
\;\;\;\;\;\;\;\;\;\;\;\;\; = \frac{1}{m}\sum\limits_{i = 1}^m {E({x^{(i)}})} - \mu \\
\;\;\;\;\;\;\;\;\;\;\;\;\; = \frac{1}{m}\sum\limits_{i = 1}^m \mu - \mu = 0
\end{array}
\]
\(\;\;\;\;\;\)从而可以确认样本均值为高斯均值的无偏估计。同理,我们可通过计算偏差来判断高斯样本方差是否为高斯方差的无偏估计:
\[\begin{array}{l}
E(\hat \sigma _m^2) = E\left[ {\frac{1}{m}\sum\limits_{i = 1}^m {{{\left( {{x^{(i)}} - {{\hat \mu }_m}} \right)}^2}} } \right]\\
\;\;\;\;\;\;\;\;\;\; = E\left[ {\frac{1}{m}\sum\limits_{i = 1}^m {{{\left( {\left( {{x^{(i)}} - \mu } \right) - \left( {{{\hat \mu }_m} - \mu } \right)} \right)}^2}} } \right]\\
\;\;\;\;\;\;\;\;\;\; = E\left[ {\frac{1}{m}\sum\limits_{i = 1}^m {\left( {{{\left( {{x^{(i)}} - \mu } \right)}^2} - 2\left( {{x^{(i)}} - \mu } \right)\left( {{{\hat \mu }_m} - \mu } \right) + {{\left( {{{\hat \mu }_m} - \mu } \right)}^2}} \right)} } \right]\\
\;\;\;\;\;\;\;\;\;\; = E\left[ {\frac{1}{m}\sum\limits_{i = 1}^m {{{\left( {{x^{(i)}} - \mu } \right)}^2}} - \frac{2}{m}\left( {{{\hat \mu }_m} - \mu } \right)\sum\limits_{i = 1}^m {\left( {{x^{(i)}} - \mu } \right)} + \frac{1}{m}\sum\limits_{i = 1}^m {{{\left( {{{\hat \mu }_m} - \mu } \right)}^2}} } \right]\\
\;\;\;\;\;\;\;\;\;\; = E\left[ {{\sigma ^2} - \frac{2}{m}\left( {{{\hat \mu }_m} - \mu } \right)\left( {m{{\hat \mu }_m} - m\mu } \right) + {{\left( {{{\hat \mu }_m} - \mu } \right)}^2}} \right]\\
\;\;\;\;\;\;\;\;\;\; = E\left[ {{\sigma ^2} - 2{{\left( {{{\hat \mu }_m} - \mu } \right)}^2} + {{\left( {{{\hat \mu }_m} - \mu } \right)}^2}} \right]\\
\;\;\;\;\;\;\;\;\;\; = {\sigma ^2} - E\left[ {{{\left( {{{\hat \mu }_m} - \mu } \right)}^2}} \right]\\
\;\;\;\;\;\;\;\;\;\; = {\sigma ^2} - D\left[ {{{\hat \mu }_m}} \right]\\
\;\;\;\;\;\;\;\;\;\; = {\sigma ^2} - D\left[ {\frac{1}{m}\sum\limits_{i = 1}^m {{x^{(i)}}} } \right]\\
\;\;\;\;\;\;\;\;\;\; = {\sigma ^2} - \frac{1}{{{m^2}}} \cdot m{\sigma ^2} = \frac{{m - 1}}{m}{\sigma ^2}
\end{array}
\]
即\(bias(\hat \sigma _m^2) = E(\hat \sigma _m^2) - {\sigma ^2} = - \frac{1}{m}{\sigma ^2}\),所以样本方差\(\hat \sigma _m^2{\rm{ = }}\frac{1}{m}\sum\limits_{i = 1}^m {{{\left( {{x^{(i)}} - {{\hat \mu }_m}} \right)}^2}}\)为\({\sigma ^2}\)有偏估计,无偏样本方差为\(\hat \sigma _m^2{\rm{ = }}\frac{1}{{m{\rm{ - }}1}}\sum\limits_{i = 1}^m {{{\left( {{x^{(i)}} - {{\hat \mu }_m}} \right)}^2}}\)。
\(\;\;\;\;\;\)以上便是对偏差概念的介绍,偏差可用于判断估计与实际值之间的误差,同时也顺带推导了关于样本方差的无偏估计为什么是除以(n-1)的问题。但是通过偏差有时并不能很好的判断估计的误差,我们可以将估计量作为数据样本的函数,估计量期望的变化程度同样是衡量估计误差的重要指标。我们可通过计算估计量的方差来表示:\({\rm{Var}}(\hat \theta )\),标准差表示为:\(SE(\hat \theta )\)。根据上式,可以得到均值的标准差:
\[SE(\hat \theta ) = \sqrt {{\rm{Var}}\left[ {\frac{1}{m}\sum\limits_{i = 1}^m {{x^{(i)}}} } \right]} = \frac{\sigma }{{\sqrt m }}
\]
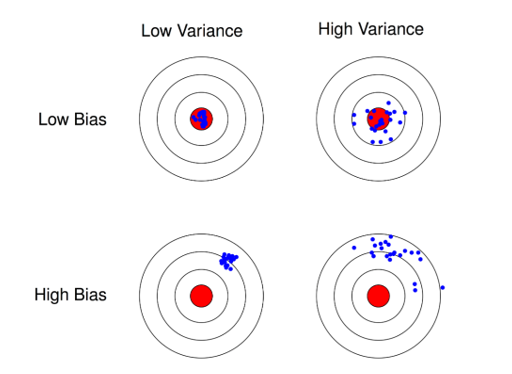
\(\;\;\;\;\;\)关于偏差与方差的区别以及各自在估计误差中的体现可通过下图理解,假设红色的靶心区域是学习算法完美的正确预测值, 蓝色点为每个数据集所训练出的模型对样本的预测值。当我们从靶心逐渐向外移动时, 预测效果逐渐变差;很容易看出有两副图中蓝色点比较集中, 另外两幅中比较分散, 它们描述的是方差的两种情况. 比较集中的属于方差小的, 比较分散的属于方差大的情况;再从蓝色点与红色靶心区域的位置关系, 靠近红色靶心的属于偏差较小的情况, 远离靶心的属于偏差较大的情况。
![]()
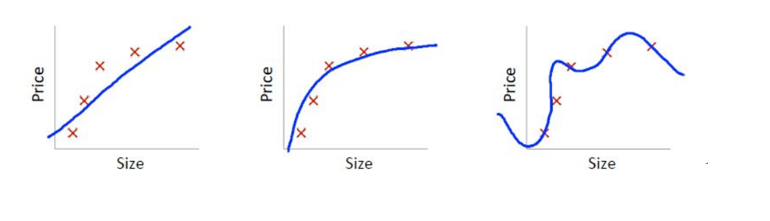
\(\;\;\;\;\;\)那模型和偏差、方差之间的对应关系是什么样呢?以回归任务为例,看一个极端例子,y=c,不论模型的训练数据如何变化,学得的函数都不会变,因此f(x;D)的输出都相同,即模型的稳定性非常好,但是对训练集的拟合也不是很好,显然对于测试样本的预测也不会很准确,这种对训练集刻画不足的情况,称为欠拟合(underfitting)。逐渐增加模型的复杂度,学得的函数对训练数据的拟合越来越好。
![]()
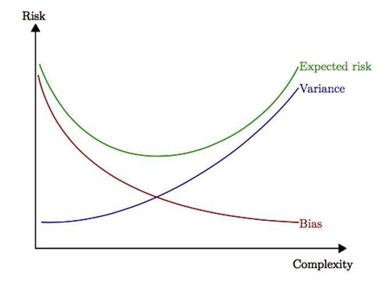
\(\;\;\;\;\;\)但是,对于一个复杂的模型,当我们稍微改变训练样本时,学得的函数差距将非常的大。这说明复杂的模型对训练样本拟合很好,但是模型的波动性也很大,很可能在测试样本的表现非常差。可以理解为,复杂的模型将训练样本的特性当作全体样本的通性,将噪声引入了模型中,这种现象称之为过拟合(overfitting)。所以我们需要在模型复杂度之间权衡,使偏差和方差得以均衡(trade-off),这样模型的整体误差才会最小。
![]()
\(\;\;\;\;\;\)这里,我们可以通过均方误差来权衡偏差与方差,MSE的估计包含了偏差和方差两项,具有较小的均方误差可以一定程度上约束偏差和方差。
\[{\rm{MSE = }}E\left[ {{{\left( {{{\hat \theta }_m} - \theta } \right)}^2}} \right] = {\rm{Bias}}{\left( {{{\hat \theta }_m}} \right)^2} + {\rm{Var}}\left( {{{\hat \theta }_m}} \right)
\]


 浙公网安备 33010602011771号
浙公网安备 33010602011771号