TOJ 4701 求阴影部分面积

4701: 求阴影部分面积 

本文版权归BobHuang和博客园共有，不得转载。如想转载，请联系作者，并注明出处。

Time Limit(Common/Java):1000MS/3000MS     Memory Limit:65536KByte
Total Submit: 63            Accepted:40

Description

 

设正方形ABCD边长为a，分别以B和D为圆心，绘制半径为a的1/4圆，与正方形的内切圆相交与M、N、O、P点，求这些交点围成的阴影部分面积。

 

Input

 

输入数据有多组，每组输入一个正整数a(a<=20)，表示正方形的边长，输入以EOF结束。

 

Output

 

每组输出一个小数，表示阴影部分的面积，保留为2位小数

 

Sample Input

 2

Sample Output

 1.97

Hint

 圆周率PI取acos(-1.0)

Source

数信学院第六届新生程序设计竞赛

这个几何挺经典的，其实主要是利用了一个特殊的三角形。圆心角是圆周角的二倍

以前我在我博客里写过答案，现在一时间还真的竟然是推不出来的

 

 

 

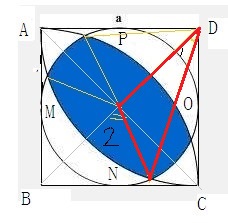
写一下推演过程

红色三角形的三边是已知的，分别是1，√2，2

然后根据余弦定理求出∠1，∠2是∠1的两倍

有一个要求的扇形显而易见，其角度也能很快得到

本文版权归BobHuang和博客园共有，不得转载。如想转载，请联系作者，并注明出处。

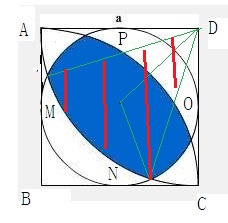
减去两个三角形就是一半面积的一部分

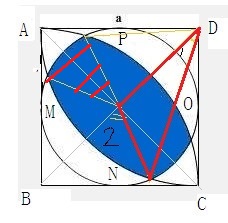
一半的阴影剩下的一部分如上图所示

两个扇形找到了，三角形也可以求出来，直接手算出cosa啥的

很简单

求三角形面积 
{ 
double a=1.0,b=2.0,c=sqrt(2.0),s,area; 
s=(a+b+c)/2; 
area=sqrt(s*(s-a)*(s-b)*(s-c)); 
printf(“area=%.12f”,area); 
} 
求一份的面积 
{double PI=acos(-1.0); 
double a1=acos(1.25/sqrt(2.0)); 
double a2=acos(-0.5/sqrt(2.0))-PI/2.0; 
double s=a1*2+a2/2-0.661437827766; 
printf(“%.12f”,s); 
}

因为a只有20,所以这样做的精度就没有问题，否则等比列变幻上去就好了

ac代码

#include <stdio.h>
int main()
{  int a;
   while(~scanf("%d",&a)){
   a*=1.0;
   printf("%.2f\n",0.492635644*a*a);}
    return 0;
}