算法竞赛 | 组合数学之盒子和球

本博客原文地址：https://www.cnblogs.com/BobHuang/p/14979765.html，原文体验更佳

组合数学中盒子和球存在以下模型，很多问题都来源自以下模型，可以尝试推出公式并写出代码。

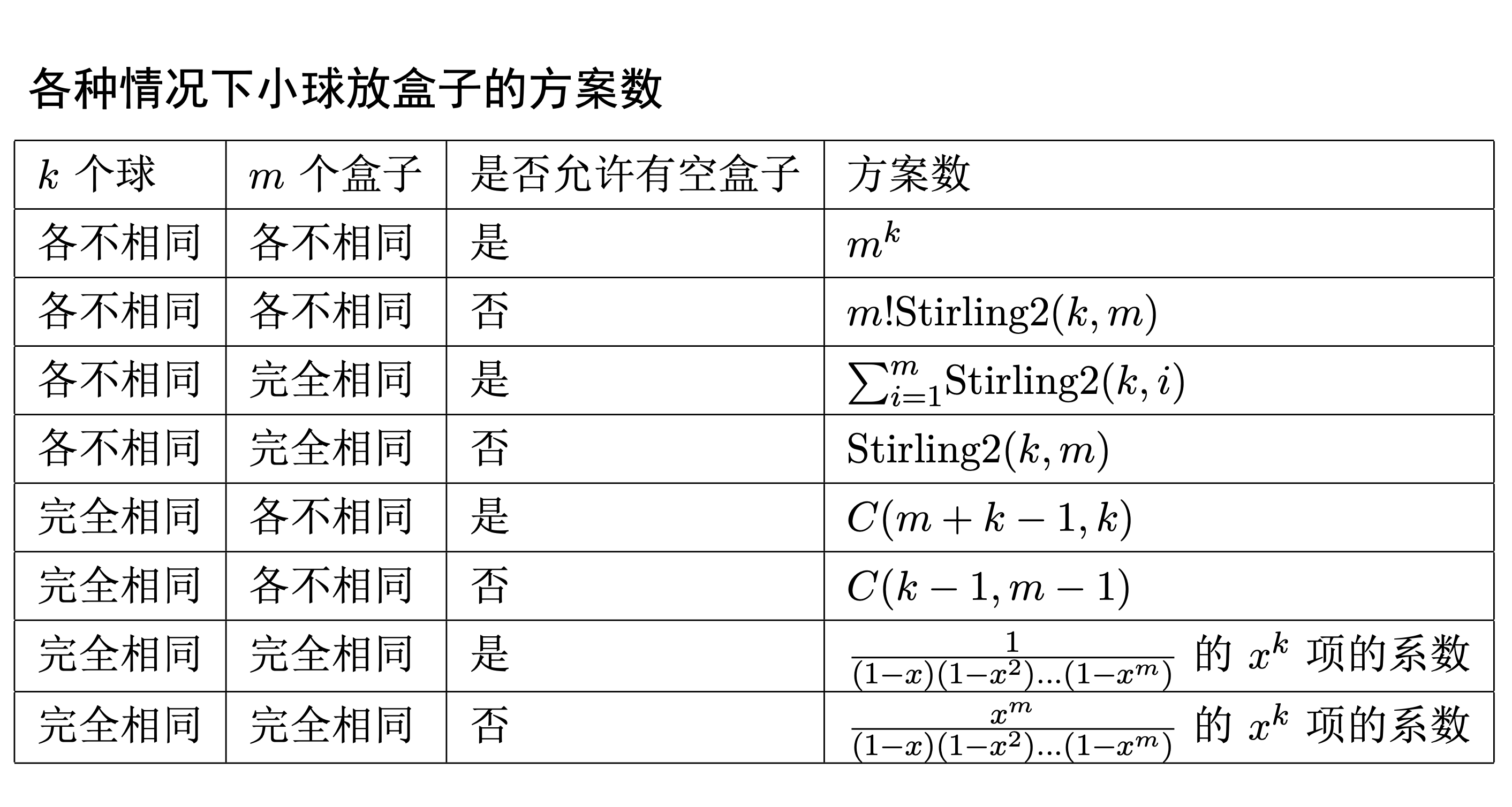
一、TZOJ6980: 盒子和球1

给定k个有标号的球，标号依次为1，2，…，k。将这k个球放入m个不同的盒子里，允许有空盒，求放置方法的总数。

每个球放进盒子中均有m种方法，所以共 \(m^k\)种。

6980参考代码

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int k,m;
    while(cin>>k>>m)
    {
        long long ans=1;
        //每个球均有m种放法
        for(int i=0;i<k;i++)
        {
            ans=ans*m;
        }
        cout<<ans<<"\n";
    }
}

二、TZOJ7068: 盒子和球6

给定k个完全相同的球，将这k个球放入m个各不相同的盒子里，不允许有空盒，求放置方法的总数。

不允许有空盒，如果球数<盒子数，放不下，直接输出为0。

接下来我们考虑把k个球分进m个盒子里，其实就是我们的隔板法。k个球有k-1个空，x个板子可以分为x+1份，要分为m份需要m-1个板子。

所以可以等价为k-1个空要插入m-1个板子，也就是k-1个中选m-1个，即\(C(k-1,m-1)\)

7068参考代码

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
LL fac(int n)
{
    LL ans=1;
    for(int i=1;i<=n;i++)
    {
        ans=ans*i;
    }
    return ans;
}

LL cal_C(int n,int m)
{
    if(m>n)return 0;
    return fac(n)/fac(n-m)/fac(m);
}
int main()
{
    int k,m;
    while(cin>>k>>m)cout<<cal_C(k-1,m-1)<<"\n";
    return 0;
}

三、TZOJ7067: 盒子和球5

给定k个完全相同的球，将这k个球放入m个各不相同的盒子里，可以有空盒，求放置方法的总数。

与盒子和球6相比多了可以有空盒，可以有空盒需要怎么理解呢。我们把盒子数也加上，也就是把球和板子看成同一种物体，有m+k-1个，其中k个空位放球，m-1个空位放板子，那么在这m+k-1空位中，放k个球的方案数就是\(C(m+k-1, k)\)；放球和放板子是等价的，当然也可以是\(C(m+k-1, m-1)\)；因为\(C(n, m)=C(n, n-m)\)，所以\(C(m+k-1, k)=C(m+k-1, m-1)\)。

我们能不能考虑将球放进分别放进1、2、....、m个箱子呢，即\(\sum\limits_{i=1}^m C(k-1,i-1)\)，但是这样却是错误的，为什么呢？因为盒子是不同，这样直接相加忽略了每次选盒子的过程。
正确的答案是 \(\sum\limits_{i=1}^m C(k-1,i-1)\times{C(m,i)}\)，这个式子和\(C(m+k-1, k)\)等价，建议证明一下。

四、TZOJ6334: 盒子和球4

k个不同球放进m个相同的盒子，不允许有空盒的方案数。

由于球有序号，我们需要考第i个球放进j个盒子的放法\(S(i,j)\)。

若单独放一盒也就是和第i个球放进j-1个盒子一样一样，即\(S(i-1,j-1)\)；否则我们需要在第i-1个盒子放进j个盒子种任选一个盒子放，即\(j\times{S(i-1,j)}\)。

然后可以分析下初始条件，若1个盒子就全放进去也就是1种方法，若球数<盒子数，那就无法放了，也就是0。

所以我们可以写出递归代码，避免递归次数太多，我们需要记忆化一下。

6334参考代码1

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
LL ans[16][16];
LL S(LL k, LL m)
{
    if(k<m)
        return 0;
    if(ans[k][m])return ans[k][m];
    //1个盒子，全放进去
    if(m==1)return 1;
    //单独一盒+放进r个盒子里
    return ans[k][m]=S(k-1, m-1)+m*S(k-1, m);
}

int main()
{
    LL k, m;
    while(cin>>k>>m)
    {
        cout<<S(k, m)<<endl;
    }
    return 0;
}

动态规划写法

只需要考虑初始状态，1个盒子放1个有1种方法，j<=i时\(dp[i][j]=dp[i-1][j-1]+dp[i-1][j]\times{j}\)，剩余都是0种

6334参考代码2

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
LL dp[16][16];

int main()
{
    dp[1][1]=1;
    for(int i=2;i<=15;i++)
    {
        for(int j=1;j<=i;j++)
        dp[i][j]=dp[i-1][j-1]+dp[i-1][j]*j;
    }
    int k, m;
    while(cin>>k>>m)
    {
        cout<<dp[k][m]<<endl;
    }
    return 0;
}

这就是大名鼎鼎的第二类斯特林数，在组合数学运用广泛。存在通项公式

\[S(n, m)=\sum\limits_{i=0}^m \dfrac{(-1)^{m-i}i^n}{i!(m-i)!} \]

这个式子可以用容斥原理证明，有兴趣可以尝试下。根据此通项公式就可以利用卷积或生成函数将以上\(O(n^{2})\)的代码优化为\(O(n\log n)\) 了。

五、TZOJ6335: 盒子和球2

给定k个不同球放入m个不同的盒子里，不允许有空盒，求放置方法的总数。

和盒子与球不同的在于盒子有了差异。
1.先考虑盒子，盒子不同，盒子的全排列数为 \(m!\)

2.再考虑球，也就是我们的盒子和球4。

分步满足乘法原理，两个相乘\(m!\times{S(k,m)}\)即为答案

六、TZOJ6981: 盒子和球3

将k个不同球放入m个相同的盒子里，可以有空盒，求放置方法的总数。

允许有空盒，我们可以考虑将其放进1，2，…，m个盒子，放进i个盒子等同于盒子和球4了，满足加法原理，求和为$$\sum\limits_{i=1}^m S(k,m)$$

为什么盒子和球4直接推广到盒子和球3没出错，但是盒子和球6直接推广到盒子和球5却出现问题了呢？因为盒子和球3、4是相同的盒子，但是盒子和球4、5盒子不同，需要考虑选的盒子种数。

七、TZOJ7307: 盒子和球7

将k个相同球放入m个相同的盒子里，可以有空盒，求放置方法的总数。

这个问题其实就是整数拆分，我们可以考虑 k 划分成 m 个自然数的可重集的方案数P(k,m)。

P(i,j)代表将i划分成j个自然数。
1.加入一个0，即放置一个空盒，要从 i 划分成 j-1 个自然数转移过来，即P(i,j-1)。

2.将j个自然数同时+1，即每个盒子都再放1个球。要从 i-j 划分成 j 个自然数转移过来，即P(i-j,j)。

然后我们考虑下初始状态，i划分为1个自然数为1。dp[i-j][j]当i-j=0时，是多了一种方案的，所以要从0开始。

TZOJ6981参考代码1

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=16;
LL dp[N][N];
int main()
{
    for(int i=0;i<N;i++)
    {
        dp[i][1]=1;
        for(int j=2;j<N;j++)
        {
            dp[i][j]=dp[i][j-1];
            if(i>=j)dp[i][j]+=dp[i-j][j];
        }
    }
    int k,m;
    while(cin>>k>>m)cout<<dp[k][m]<<"\n";
    return 0;
}

同理也可以递归去记忆化

TZOJ6981参考代码2

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=16;
LL dp[N][N];
LL dfs(int n,int m)
{
    //越界的判断掉
    if(n<0)return 0;
    //求出来过的判断掉
    if(dp[n][m])return dp[n][m];
    //放进0个球or放进1个盒子都有1种
    if(n==0||m==1)return 1;
    return dp[n][m]=dfs(n,m-1)+dfs(n-m,m);
}
int main()
{
    int k,m;
    while(cin>>k>>m)cout<<dfs(k,m)<<"\n";
    return 0;
}

有点类似于背包，想要求出其多项式可以先求 ln ，加起来再 exp 回去。

八、TZOJ7308: 盒子和球8

将k个相同球放入m个相同的盒子里，不允许有空盒，求放置方法的总数。

NOIP2001 提高组 T2 数的划分也是我们的老朋友了，和这个问题是相同的。

和盒子和球7不同点在于不允许为空，那我们就该修改自己的状态转移方程。

不能放置空盒了，但是我们可以放一个1。Q(i,j)代表将i划分成j个正数。

1.加入一个1，即放置一个盒子球个数为1。要从 i-1 划分成 j-1 个正数转移过来，即Q(i-1,j-1)。

2.将j个正数同时+1，即每个盒子都再放1个球。要从 i-j 划分成 j 个正数转移过来，即S(i-j,j)。

然后我们考虑下初始状态，i(i>0)划分为1个正数为1。dp[i-j][j]当i-j=0时，不多方案的，从1开始即可。

九、扩展

若允许每个盒子至多装一个球呢，会再多4种。再增大数据范围呢，需要多项式优化，TZOJ7309: 十二重计数法等你来挑战。