【题解】P3354 [IOI2005]Riv 河流 - 树形 $dp$ - 孩子兄弟表示法
P3354 [IOI2005]Riv 河流
声明:本博客所有题解都参照了网络资料或其他博客,仅为博主想加深理解而写,如有疑问欢迎与博主讨论✧。٩(ˊᗜˋ)و✧*。
题目描述
几乎整个 \(Byteland\) 王国都被森林和河流所覆盖。小点的河汇聚到一起,形成了稍大点的河。就这样,所有的河水都汇聚并流进了一条大河,最后这条大河流进了大海。这条大河的入海口处有一个村庄——名叫 \(Bytetown\)。
在 \(Byteland\) 国,有 \(n\) 个伐木的村庄,这些村庄都座落在河边。目前在 \(Bytetown\),有一个巨大的伐木场,它处理着全国砍下的所有木料。木料被砍下后,顺着河流而被运到 \(Bytetown\) 的伐木场。\(Byteland\) 的国王决定,为了减少运输木料的费用,再额外地建造 \(k\) 个伐木场。这 \(k\) 个伐木场将被建在其他村庄里。这些伐木场建造后,木料就不用都被送到 \(Bytetown\) 了,它们可以在运输过程中第一个碰到的新伐木场被处理。显然,如果伐木场座落的那个村子就不用再付运送木料的费用了。它们可以直接被本村的伐木场处理。
注:所有的河流都不会分叉,形成一棵树,根结点是 \(Bytetown\)。
国王的大臣计算出了每个村子每年要产多少木料,你的任务是决定在哪些村子建设伐木场能获得最小的运费。其中运费的计算方法为:每一吨木料每千米 \(1\) 分钱。
\(\\\)
\(\\\)
\(Solution\)
先从正常的套路树形 \(dp\) 方程想起,设 \(dp[i][j]\) 表示在 \(i\) 即 \(i\) 子树中建立 \(j\) 个伐木场的代价
但是这样是无法转移的——对于每个 \(dp[i][j]\) 无法得知那些未被解决的木头的贡献,如果设 \(g[i][j]\) 来记录未被解决的木头书的话,那这个是有后效性的,也就是说,每个 \(i\) 的状态对于不同的 \(i\) 的祖先的影响是不同的,无法正常 \(dp\)
为了把后效性消除掉,我们必须得知一个祖先的状态来处理掉这些未被解决的木头
顺理成章的 (但是如果没有写过这种带祖先状态的树形 \(dp\) 应该还是不容易想到的,比如我233)我们加一维状态变为 \(dp[i][j][l]\) 表示在 \(i\) 即 \(i\) 子树中建立 \(j\) 个伐木场,且从 \(i\) 往祖先方向走 \(l\) 步会碰到第一个伐木场
由于我们可以从方程中得到最近的一个祖先是谁,所以那些未被解决的木头的费用是固定的,可计算的,即可 \(dp\)
搬运代码来自:Link
void dfs(int i){
stack[++size]=i;
for(int tmp=head[i];tmp;tmp=nxt[tmp]){
int v=point[tmp];
deep[v]=deep[i]+weight[tmp];
dfs(v);
for(int j=1;j<=size;j++)
for(int k=K;k>=0;k--){
f[i][stack[j]][k]+=f[v][stack[j]][0];
g[i][stack[j]][k]+=f[v][i][0];
for(int x=0;x<=k;x++){
f[i][stack[j]][k]=min(f[i][stack[j]][k],f[i][stack[j]][k-x]+f[v][stack[j]][x]);
g[i][stack[j]][k]=min(g[i][stack[j]][k],g[i][stack[j]][k-x]+f[v][i][x]);
}
}
}
//这里是将f和g合并了,因为之后就不在乎i有没有建伐木场,只关心i和i的子树建了多少。
for(int j=1;j<=size;j++)
for(int k=0;k<=K;k++){
if(k>=1)
f[i][stack[j]][k]=min(f[i][stack[j]][k]+sum[i]*(deep[i]-deep[stack[j]]),g[i][stack[j]][k-1]);
//这里是g[i][stack[j]][k-1]的原因是:因为我们之前算g的时候,是假设i上有伐木场。而我们实际上没有把这个伐木场的数量加进去。所以合并前g[i][j][k]实际上代表的是g[i][j][k+1]
else
f[i][stack[j]][k]+=sum[i]*(deep[i]-deep[stack[j]]);
}
size--;
}
完结撒花✿✿ヽ(°▽°)ノ✿
才不会233
看标题显然发现还有另一个超可爱超有趣超神奇的!内容
你每次写树形 \(dp\) 的儿子合并都要为各种边界烦恼吗?
你厌倦了链式前向星存边吗?
来试试孩子兄弟表示法吧!(牛津高中英语M4U1套句 qwq
参考博客:Link
对于每个节点,保存四个值:\(bro\) - 指向这个点一个兄弟,\(son\) - 指向这个点的儿子,\(fa\) - 指向这个点的父亲,\(edge\) - 保存这个点与父亲的边权值
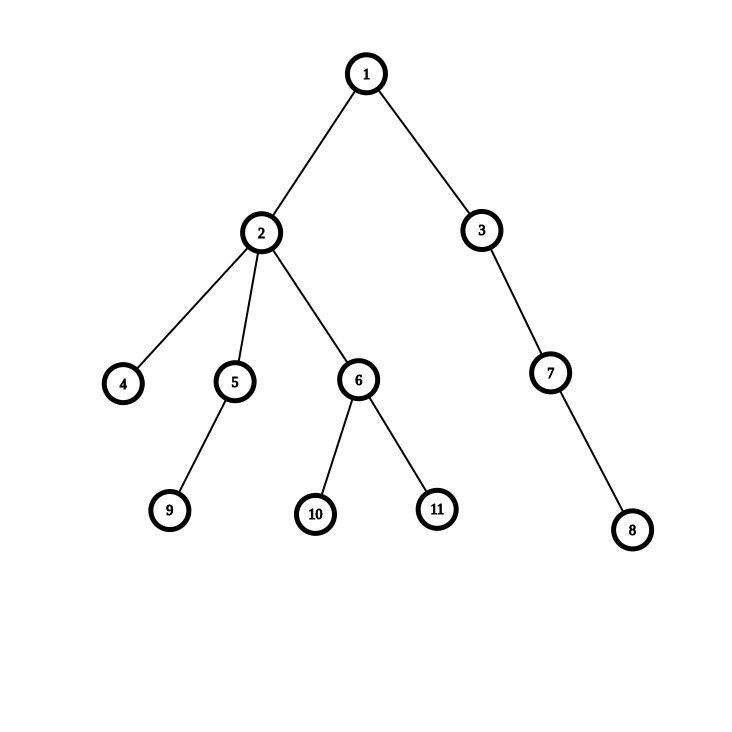
例如在这个图中,\(4, 5, 6\) 分别为兄弟,\(3\) 为 \(7\) 的父亲,\(8\) 为 \(7\) 的儿子
那么用孩子兄弟表示法就会转化为下面这张图
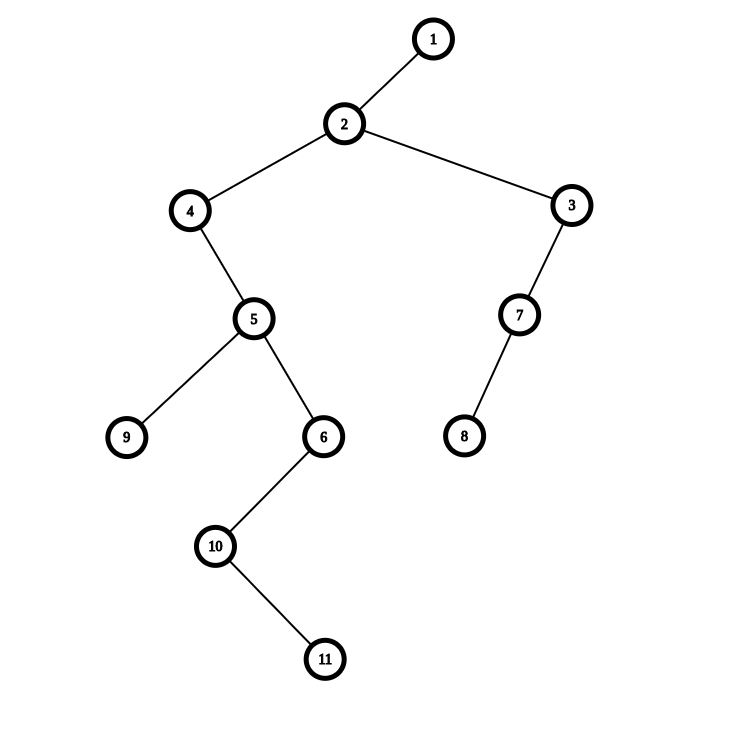
发现这是一个二叉图,为了方便理解,此张图中每个点指向的左儿子为它的儿子,右儿子为它的兄弟
关于如何构建这颗树:
for(int i = 1; i <= n; ++ i) fa[i] = read(), bro[i] = son[fa[i]], son[fa[i]] = i;
我们按照这样的树进行 \(dfs\) 时,它的一些兄弟就暂时的成为了它的子树的一部分,而在这道题中,由于兄弟间是互相不影响的,所以一个节点可以存储它兄弟的信息,同时可以更新它另外一些兄弟的信息,因为这些兄弟们总是在它们的父亲的子树中的,所以答案总会被更新出来
那么这样写有什么好处呢?!
上代码啦啦啦(∇*)
void dfs(int x, int dep)
{
int bro = b[x], son = s[x];
F(i, 1, dep) dis[x][i] = dis[f[x]][i - 1] + e[x];
if(bro) dfs(bro, dep);
if(son) dfs(son, dep + 1);
F(i, 0, k)
F(j, 0, k - i)
F(l, 1, dep)
{
dp[x][i + j][l] = min(dp[x][i + j][l], dp[bro][i][l] + dp[son][j][l + 1] + w[x] * dis[x][l]);
dp[x][i + j + 1][l] = min(dp[x][i + j + 1][l], dp[bro][i][l] + dp[son][j][1]);
}
}
对比上面的代码可以直观地发现,这样子省去了各种合并,由于每个结点只有两个儿子,就用两个循环更新即可!
最后的答案就是 \(dp[son[0]][k][1]\) ~
真——完结撒花✿✿ヽ(°▽°)ノ✿
\(\\\)
\(\\\)
\(Code\)
#include<bits/stdc++.h>
#define F(i, x, y) for(int i = x; i <= y; ++ i)
using namespace std;
int read();
const int N = 105;
int n, k, dp[N][55][N];
int b[N], s[N], f[N], e[N], w[N], dis[N][N];
void dfs(int x, int dep)
{
int bro = b[x], son = s[x];
F(i, 1, dep) dis[x][i] = dis[f[x]][i - 1] + e[x];
if(bro) dfs(bro, dep);
if(son) dfs(son, dep + 1);
F(i, 0, k)
F(j, 0, k - i)
F(l, 1, dep)
{
dp[x][i + j][l] = min(dp[x][i + j][l], dp[bro][i][l] + dp[son][j][l + 1] + w[x] * dis[x][l]);
dp[x][i + j + 1][l] = min(dp[x][i + j + 1][l], dp[bro][i][l] + dp[son][j][1]);
}
}
int main()
{
n = read(), k = read();
F(i, 1, n)
{
w[i] = read(), f[i] = read(), e[i] = read();
b[i] = s[f[i]], s[f[i]] = i;
}
memset(dp, 0x3f, sizeof(dp));
F(i, 0, k) F(j, 0, n) dp[0][i][j] = 0;
dfs(s[0], 1), printf("%d\n", dp[s[0]][k][1]);
return 0;
}
int read()
{
int x = 0, f = 1;
char c = getchar();
while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
return x * f;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号