【学习笔记】零碎知识点记录
前言
想记录一下学了的东西,我金鱼记忆真是学啥忘啥。。。
干啥啥不行,喝奶茶第一名
\(\\\)
\(\\\)
\(2020.7.22\)
暑假期间改为笔记了qwq(教练要检查 雾
\(\\\)
\(\\\)
"中值滤波"
据某位巨佬说是叫这个名字,但是到百度上搜真是一脸懵逼...大概和傅里叶变换情况差不多。
是啥
只能用不严谨的语言描述一下...
对于一个数字序列 \(a\) ,有一个对应 \(01\) 字符串 \(s\) ,其中 \(s[i] \ = \ (a[i] \ >= \ k)\) ,\(k\) 为给定值
对于 \(01\) 字符串 \(s\) ,做一个变换,规则是,当 \(i \ = \ 1 || i \ = \ len\) 时,不变换,剩余 \(s[i]\) 变换为 \((s[i - 1], s[i], s[i + 1])\) 中的中位数
三个性质
\(1.\) \(0\) 和 \(1\) 交替出现的奇数串:若两端是 \(0\) 则最后变换完为全 \(0\);两端为 \(1\) 则最后变换完为全 \(1\)
\(2.\) \(0\) 和 \(1\) 交替出现的偶数串:若左端是 \(0\) ,变换完为左半部分全 \(0\),右半部分全 \(1\);若左端是 \(1\) ,变换完为左半部分全 \(1\),右半部分全 \(0\)
\(3.\) 连续的一串 \(0\) 或 \(1\):变换为仍为它本身
任何一个 \(01\) 串都可以划分为上面三种情况,从而快速求出变换完的情况
应用
\(test0710\) - 数字三角形
\(\\\)
\(\\\)
有关 \(STL - map\)
查询 \(map\) 中某个状态是否存在时,直接用 if(mp[S]) balabala; 的话,其实会在 \(map\) 里新开一个空间
正确的做法是
map<int, int>::iterator k = num.find(i); //定义一个迭代器
k->first = i;//k->first 里面存的是 i ,也就是下标
k->second = num[i];//k->second 里面存的是 num[i] ,也就是原值
k = num.end();//如果 map 中没有过这个状态,那么 k 就等于 num.end()
\(\\\)
\(\\\)
\(splay\)
\(\\\)
\(\\\)
\(Tarjan\) 割点
为什么是low[u] = min(low[u], dfn[v]);而不是low[u] = min(low[u], low[v])
我的理解是,如果你通过 \(v\) 去找到了更远的祖先,那之后想把 \(v\) 删除时,就无法记录 \(v\) 的答案了,因为 \(low[u]\) 里存的东西是已经经过了 \(v\) 的
\(\\\)
\(\\\)
\(Manacher\)
最开始感觉这是个暴力玄学算法...最后发现它居然是严格 \(O(n)\) 的233
分两种情况讨论:
对于某个位置的字符,
若右边界不需要扩展,那么 \(p[i]\) 其实是直接由右边界那里转移过来了,而无法再扩展,因为它的对应点已经扩展完了,及为 \(O(1)\)
若右边界需要扩展,那么在整个算法中,右边界是从 \(0\) 一直到 \(n - 1\) 的,总复杂度是 \(O(n)\)
所以最后应该是 \(O(2n)\) 的
\(\\\)
\(\\\)
泰勒展开
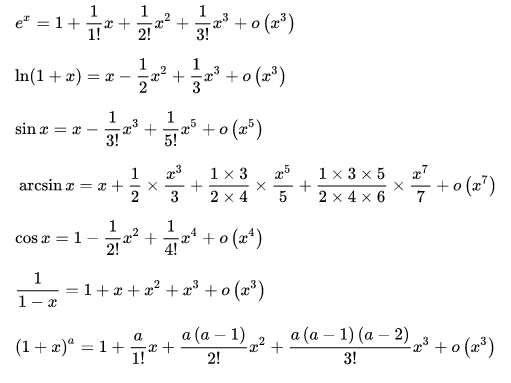
\(\\\)
\(\\\)
二项式定理

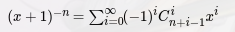
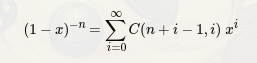
学习博客
\(\\\)
\(\\\)
波利亚瓦罐模型

\((3)\)
设 \(k\) 为第 \(k\) 次取得黑球的事件,\(A\) 为第一次取得黑球的事件
先假设一个结论, \(P(k) = \frac{n_1}{n_1 + n_2}\),\(n_1, n_2\) 为初始堆里黑球白球的数量,利用数学归纳法,若 \(P(k + 1)\) 也成立,那么这个结论成立
利用全概率公式得
\(P(k + 1) = P(k + 1 | A) * P(A) + P(k + 1 | \overline{A}) + P(\overline{A})\)
\(P(k + 1 | A)\) 可以理解为,固定原始堆里有 \(n_1 + r\) 个黑球,\(n_1 + n_2 + r\) 个球,然后取 \(k\) 次
即
证得 \(P(k + 1)\) 也满足上述结论,则 \(P(k) = \frac{n_1}{n_1 + n_2}\) 成立
\(\\\)
\(\\\)
裴蜀定理
内容
若有 \(ax + by = c\) ,且 \(x, y\) 都为整数,那么 \(\gcd(x, y)|c\) ,且 \(a, b\) 一定有整数解
证明有点简单233,不写了
推广
可以推广到多个数,及 \(a_1x_1 + a_2x_2 + ... + a_ix_i = c \ , \ \gcd(x_1, x_2...x_i)|c\)
\(\\\)
\(\\\)
矩阵树 \(Matrix-Tree\)
·对于一个无向图 \(G\) ,它的生成树个数等于其 基尔霍夫\(Kirchhoff\)矩阵 任何一个 \(N - 1\) 阶主子式的行列式的绝对值。
·所谓的 \(N - 1\) 阶主子式就是对于一个任意的一个 \(r\) ,将矩阵的第 \(r\) 行和第 \(r\) 列同时删去得到的新矩阵。
·基尔霍夫\(Kirchhoff\)矩阵 \(K\) \(=\) 度数矩阵 \(D\) (仅在 \((i, i)\) 处为点 \(i\) 的度数,其余为零) \(-\) 邻接矩阵 \(A\) (就是图的那个邻接矩阵)
\(\\\)
\(\\\)
行列式
性质 \(1\):
设矩阵 \(T_1, T_2\)
虽然矩阵不满足乘法交换律,即 \(T_1T_2 \neq T_1T_2\)
但是 \(\det (T_1T_2) = \det (T_1T_2)\)
感性理解:可以把两个矩阵看做两个线性变换,先做 \(T_1\) 或 \(T_2\) 最后表现出来的矩形其实是一样的,而此处行列式可表示为矩形的面积,所以矩形的面积是相同的,即行列式相同
性质 \(2\)
设矩形 \(A, B\),则有 \(\det (AB) = \det(A) · \det(B)\)
简单证明:可以设 \(A, B\) 为二阶矩阵,直接代入然后按照行列式计算方式算就好了(至于如何从特殊到一般嘛...太菜了 \(/kk\)
性质 \(3\)
把行列式里的某两行/某两列交换,行列式变号
证明:首先,行列式里忽略符号的话,每一项是没变的;关于符号...太菜了 \(/kk\)
记录一个证明(虽然没太看懂233

性质 \(4\)
当行列式里有两行完全一样时,行列式 $ = 0$ (简单证明:交换这两行,行列式要变号,就只能等于零)
性质 \(5\)
当行列式里有两行成比例时,行列式 $ = 0$ (简单证明:提取出比例 \(k\) 到整个式子之前,那么式子里就有两项是相同的了,即等于零)
性质 \(6\)
当行列式里某一行加上另一行的 \(k\) 倍时,行列式的值不变(简单证明:按照行列式的加法可以把它拆成两个行列式,一个行列式为原行列式,另一个的某一行为另一行的 \(k\) 倍,行列式值为原行列式值加上零,所以不变)
性质有待补充...(怎么这么多!!大力吐槽
关于如何优化行列式的计算:
根据性质 \(6\) ,可以高斯消元得到一个倒三角类型的东西
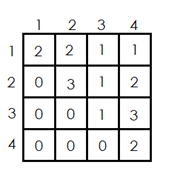
(图源学习博客)
可以发现此时行列式的值就是对角线相乘,因为其他项都有零,总共的复杂度是 \(O(n_3)\)
\(\\\)
\(\\\)
线性变换
记录一个 好棒的blog
线性代数在几何直观三个要点:
·变换前是直线,变换后仍然是直线
·直线比例保持不变
·变换前是原点,变换后仍然是原点
自己想加的:
·变换前变换后,直线都是平行的
·变换前后的系数并没有变,变的是基
如何理解矩阵相乘的几何意义:
“矩阵相乘,其几何意义就是两个线性变换的复合,比如A矩阵表示旋转变换,B矩阵表示伸长变换,AB就是伸长加旋转的总变换:同时伸长和旋转。”
\(\\\)
\(\\\)
旋转卡壳
不能用距离判断的原因:

可以构造一个三角形,易证得过任意一个点做的高,小于等于这个点的两条边(我不会!用数学语言!证明!太菜了 \(/kk\)
然后过这个点做一条射线,使这条射线过这个点的对边,把这个对边往外撑一点点,类似射箭的弓那样(我!尽!力!了!
再把这条射线变成一个向量的话,它就是有可能小于两条对边的,但这时候这三个点(图中 \(2 \ 3 \ 4\) )仍然可以是某个凸包的一部分的,但是 \(b\) 向量的模小于 \(a\) 和 \(c\) 的
所以不能用距离来维护
(淦,自己都看不下去,等之后有机会再改改
用叉积求三角形面积
\(\vec{a} \times \vec{b} = |\vec{a}| * |\vec{b}| * \sin \theta\),其中 \(|\vec{a}| * \sin \theta\) 就是 \(b\) 对应的高
用叉积除以二就是三角形面积
\(\\\)
\(\\\)
\(Pollard-Rho\)
主要思路:
按照某种方式找到 \(n\) 的一个因子,判断它是否是质数( \(Miller-Rabin\) ),是的话直接计入答案,不是则继续分解
注意!! \(floyd\) 判环先要让 \(j\) 多走一步,判一次,然后再开始循环,不然会漏情况
\(\\\)
\(\\\)
\(Miller-Rabin\)
前置知识:
\(1.\)费马小定理 \(a^{p - 1} \equiv 1 \pmod{p}\),\(p\) 为质数
\(2.\)二次探测定理,若 \(p\) 为质数,\(0 <x < p\),则 \(x^2 \equiv 1 \pmod p\) 的解为 \(x_1 = 1, x_2 = p - 1\)
二次探测定理证明:
简要步骤:
\(1.\)随机选取一个数 \(a\)
\(2.\)根据费马小定理判断 \(a^{p - 1} \equiv 1 \pmod{p}\) 是否成立,不成立则直接返回 \(false\) ,成立则进入 \(3\)
\(3.\)由于 \(a^{p - 1} \equiv 1 \pmod{p}\) ,设 \(t = \frac{p - 1}{2}\),根据二次探测定理有,\(a^t \% p\) 为 \(1\) 或 \(p - 1\),于是判断是否成立,不成立则返回 \(false\) ,成立则继续第 \(3\) 步
\(4.\)当 \(t\) 为奇数时,既无法继续二次探测,返回 \(true\),继续 \(1\) ,选择下一个数
代码:
这个代码是反着来的,应该正着反着都可以,但是网上正着的代码看不懂就写了反的emm
#include<bits/stdc++.h>
#define ll long long
#define F(i, x, y) for(int i = x; i <= y; ++ i)
using namespace std;
ll mul(ll x, ll y, ll p)
{
ll res = 0;
while(y)
{
if(y & 1)
{
res += x;
if(res >= p) res %= p;
}
x <<= 1, y >>= 1;
if(x >= p) x %= p;
}
}
ll qpower(ll x, ll y, ll p)
{
ll res = 1;
while(y)
{
if(y & 1) res = mul(x, res, p);
x = mul(x, x, p), y >>= 1;
}
return res;
}
bool Miller_Rabin(ll x)
{
if(x == 2) return true;
if(x == 1 || !(x & 1)) return false;
ll t = x - 1, k = 0;
while(!(t & 1)) ++ k, t >>= 1;
F(i, 1, 20)
{
ll a = rand() % (x - 1) + 1, b = qpower(a, t, x), c;
F(j, 1, k)
{
c = mul(b, b, x);
if(c == 1 && b != 1 && b != p - 1) return false;
b = c;
}
if(c != 1) return false;
}
return true;
}
\(\\\)
\(\\\)
莫比乌斯反演
还有 \(lsq\) 版证明:
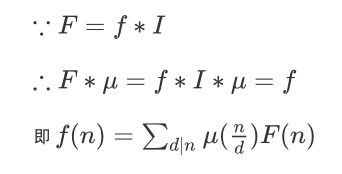
两种形式(我真的连这个都能忘的...)
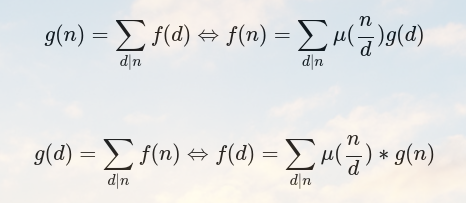
\(\\\)
\(\\\)
狄利克雷卷积
学习博客:狄利克雷卷积
关于结合律:
关于 \(\varphi (n)\) 为积性函数:
存疑:
关于性质六(逆元:对于每一个 \(f(1)≠0\) 的函数 \(f\) ,都有 \(f∗g=ϵ\) )的构造
\(\\\)
\(\\\)
整除分块
求:
两个重要性质:
\(1.\lfloor \dfrac{n}{i} \rfloor\) 最多只有 \(2 * \sqrt{n}\) 种
\(2.\)若 \(\lfloor \dfrac{n}{k} \rfloor = \lfloor \dfrac{n}{i} \rfloor\) ,则 \(i\) 最大值为 \(\lfloor \dfrac{n}{\lfloor \frac{n}{k} \rfloor} \rfloor\)
证明可以看看这篇,好强啊qwq
极其简短代码:
for(ll l = 1, r; l <= n; l = r + 1)
{
if(k / l == 0) r = n;
else r = min(n, k / (k / l));
ans += (k / l) * (r - l + 1);
}
\(\\\)
\(\\\)
线性基
\(1.\)原序列里面的任意一个数都可以由线性基里面的一些数异或得到
简单证明:
由线性基的构造得,\(x\) 在不断异或一些数后
如果二进制下不存在任何一位上为 \(1\),那么 \(x\) 就无法加入进线性基里了,即 \(x = p[i_1] \text{^} p[i_2] \text{^} ... \text{^} p[i_j]\)
如果此时 \(x\) 变成了 \(x'\),且 \(x'\) 符合加入线性基的条件,那么 \(x = p[i_1] \text{^} p[i_2] \text{^} ... \text{^} p[i_j] \text{^} x'\)
证毕
\(\\\)
\(2.\)线性基里面的任意一些数异或起来都不能得到 \(0\)
简单证明:
假设线性基中的 \(p_{i1} \text{^} p_{i2} \text{^} ... \text{^} p_{ij} = 0\)
即有\(p_{i1} \text{^} p_{i2} \text{^} ... \text{^} p_{i \ j-1} = p_{ij}\)
由线性基的构造得, \(p_{ij}\) 不可能被加入进线性基里
证毕
\(\\\)
\(3.\)线性基里面的数的个数唯一,并且在保持性质一的前提下,数的个数是最少的
简单证明:
先看个数能否增多
假设有 \(x, y\) 没有在线性基里,我们想从线性基里拿出一个数 \(z\),再把 \(x, y\) 放进去,尝试是否可行
设 \(S_x\) 和 \(S_y\) 表示线性基中异或出 \(x\) 和 \(y\) 的集合,那么 \(z\) 一定在 \(S_x\) 和 \(S_y\) 中选,如果不是那么并不会对 \(x\) 和 \(y\) 造成任何影响
如果 \(S_x \ \cap \ S_y = 0\),显然 \(x, y\) 不可能被同时放入
如果 \(S_x \ \cap \ S_y \ne 0\),那么 \(z\) 一定要在 \(S_x \ \cap \ S_y\) 中选(不在则同上)
设 \(k_1\) 为 \(S_x\) 去掉 \(z\),\(k_2\) 为 \(S_y\) 去掉 \(z\)
则有 \(k_1 \text{^} z = x\),\(k_2 \text{^} z = y\)
根据异或的性质,又有 \(k_1 \text{^} x = z\),带入进上面的式子则有 \(k_2 \text{^} k_1 \text{^} x = y\)
那么 \(y\) 还是不能加入进去,即个数无法增多
再看个数能否减少
假设我们想把 \(x\) 拿出来,那就要求 \(x = p_{i1} \text{^} p_{i2} \text{^} ... \text{^} p_{ij}\),但根据线性基的构造得,这样的 \(x\) 不可能被加入进去,即个数无法减少


 浙公网安备 33010602011771号
浙公网安备 33010602011771号