计算机算术

目录

• Floating-point number systems
• Rounding error analysis
  • Rounding a single number
  • Binary floating-point operations
  • The propagation of rounding errors
• Accuracy and stability
  • Avoiding catastrophic cancellation
  • Backward stability and numerical stability
  • Condition numbers: scalar functions
  • Condition numbers: vector functions
  • Condition numbers: algorithms
  • Overall error of a computer solution
• Problem

 

Floating-point number systems

Definition 4.1. 位置数字系统的基 base or radix of a positional numeral system 是表示数字的唯一记号的数量.

Definition 4.3. 位 bit 是计算机基本单位，只能有 $0$ 和 $1$ 两种值.

Definition 4.4. 字节 byte 是计算机信息的单位，通常包含 $8$ 位；它是计算机储存的最小单位.

 

Definition 4.7 (Floating point numbers). 浮点数 floating point number (FPN) 具有形式

$$x = \pm m\times \beta^e \tag{4.1}$$

其中 $\beta$ 是基， $e\in[L,U]$ ，有效数字 significand or mantissa $m$ 具有形式

$$m = \left(d_0+\dfrac{d_1}{\beta}+\cdots+\dfrac{d_{p-1}}{\beta^{p-1}}\right) \tag{4.2}$$

其中整数 $d_i$ 满足 $\forall i\in[0,p-1],\ d_i\in[0,\beta-1]$ ； $d_0$ 和 $d_{p-1}$ 称为最大有效数字 most significant digit 和最小有效数字 least significant digit ， $m$ 的数字串 string of digits 是字符串 $d_0.d_1d_2\cdots d_{p-1}$ ，其中 $.d_1d_2\cdots d_{p-1}$ 称为 $m$ 的小数部分 fraction .

 

Algorithm 4.8. 十进制整数转为二进制的方法

• 每次除以 $2$ ，然后记录余数，直到结果为 $0$ ，从后向前排列余数

$$97 = ((((((0\times 2+1)\times 2 + 1)\times 2 + 0) \times 2 + 0)\times 2 + 0)\times 2 + 0)\times 2 + 1 = (1100001)_2$$

十进制小数转为二进制的方法

• 每次乘 $2$ ，检查整数部分是否不大于 $1$ ，如果是就记录 $1$ ，否则记录 $0$ ，直到结果为 $0$ ，从前向后排列

$$\dfrac{2}{3} = \left(\left(\dfrac{1}{3}+1\right)\times\dfrac{1}{2^2}+1\right) \times \dfrac{1}{2} = (0.1010\cdots)_2$$

写成括号嵌套的形式更为直观.

 

Definition 4.11 (FPN systems). 浮点数系统 floating point number system $\mathcal{F}$ 是有理函数 $\mathbb{Q}$ 的真子集，由 $(\beta,p,L,U)$ 描述.

 

Definition 4.12. 一个 FPN 是正规的 normalized 如果它的有效数字 $1\le m<\beta$ .

 

Definition 4.13. 非正规数 subnormal 是 FPNs 中 $e=L,\ m\in(0,1)$ 的数，正规 FPN 系统可以通过包含非正规数扩张 extended .

 

Definition 4.14 (IEEE standard 754-2019). 当前的 IEEE 754 标准中的单精度 single precision 和双精度 double precision 浮点数有三种二进制格式和两种十进制格式；这里主要考虑 $32$ 位比特： $1$ 位符号位 $+$ $8$ 位指数 $+$ $23$ 位有效数字，精度为 $24$ ，因为我们可以在正规二进制浮点系统中取 $d_0=1$ ，然后不用存储 $d_0$ .

 

Definition 4.16. 正规 FPN 系统 $\mathcal{F}$ 的机器精度 machine precision 是 $1.0$ 到 $\mathcal{F}$ 中下一个较大的 FPN 的距离

$$\epsilon_M = \beta^{1-p} \tag{4.3}$$

按照格式整数加小数部分一共有 $p$ 位有效数字，最后一位为 $\beta^{1-p}$ .

 

Definition 4.17. 下溢极限 UFL 和上溢极限 OFL 为

$$UFL(\mathcal{F}) = \min|\mathcal{F}\setminus\{0\}| = \beta^L\\ OFL(\mathcal{F}) = \max|\mathcal{F}| = \beta^U(\beta-\beta^{1-p}) \tag{4.4}$$

下溢极限是最小的非零浮点数，上溢极限则是最大的浮点数.

 

Corollary 4.19 (Cardinality of $\mathcal{F}$ ). 对于二进制正规 FPN 系统，有

$$\#\mathcal{F} = 2^p(U-L+1) + 1 \tag{4.5}$$

$Proof.$ 注意在二进制储存时不用存 $d_0$ ，而是在这里存放符号，因此有 $2\times 2^{p-1}$ 种有效数字，同时有 $U-L+1$ 种指数，再加上 $0$ 就是所有的正规浮点数.

 

Definition 4.20. 正规 FPN 系统的范围 range 是 $\mathbb{R}$ 的子集

$$\mathcal{R}(\mathcal{F}) = \{x:x\in\mathbb{R},\ UFL(\mathcal{F})\le |x|\le OFL(\mathcal{F})\} \tag{4.6}$$

它是两段区间，分别在正半轴和负半轴；注意 $\mathcal{F}$ 不能取得范围内的所有实数.

 

Definition 4.22. 两个正规 FPNs $a,b$ 在 $\mathcal{F}$ 中相邻 adjacent 当且仅当

$$\forall c\in\mathcal{F}\setminus\{a,b\},\quad |a-b|<|a-c|+|b-c| \tag{4.7}$$

也就是两个数之间没有其它浮点数.

 

Lemma 4.23. 令两个正规 FPNs $a,b$ 在 $\mathcal{F}$ 中相邻，满足 $|a|<|b|,\ ab>0$ ，则

$$\beta^{-1}\epsilon_M|a| < |a-b|\le\epsilon_M|a| \tag{4.8}$$

$Proof.$ 考虑 $a = m\times\beta^e > 0$ ，则有 $|a-b| = \epsilon_M\beta^e$ ，由 $1.0\le m<\beta$ 有

$$\beta^{-1}\epsilon_M < \dfrac{|a-b|}{|a|} \le \epsilon_M$$

即证.

 

Rounding error analysis

Rounding a single number

Definition 4.24 (Rounding). 舍入 Rounding 是映射 $\mathrm{fl}:\mathbb{R}\to\mathcal{F}\cup\{+\infty,-\infty,NaN\}$ ，默认舍入是舍入到最近 round to nearest 的浮点数；在距离相等 tie 的情况下， $\mathrm{fl}(x)$ 选择舍入到最后一位为偶数 round to even .

 

Definition 4.25. 舍入数 $\mathrm{fl}(x)$ 上溢 overflows 若 $|x|>OFL(\mathcal{F})$ ，此时 $\mathrm{fl}(x) = NaN$ ；下溢 underflows 若 $0<|x|<UFL(\mathcal{F})$ ，此时 $\mathrm{fl}(x) = 0$ ；扩张的 FPN 系统的下溢称为渐进下溢 gradual underflow .

 

Definition 4.26. $\mathcal{F}$ 的单位舍入 unit roundoff 是

$$\epsilon_u = \dfrac{1}{2}\epsilon_M = \dfrac{1}{2}\beta^{1-p} \tag{4.9}$$

Theorem 4.27 (Range of round-off errors). 对 $x\in\mathcal{R}(\mathcal{F})$ 有

$$\mathrm{fl}(x) = x(1+\delta) \tag{4.10},\quad |\delta| < \epsilon_u$$

$Proof.$ 将浮点范围的实数舍入到 $\mathcal{F}$ 中，则我们考虑相邻的浮点数 $x_L,x_R\in\mathcal{F},\ x_L\le x\le x_R$ ，相等的情况显然；否则

$$|\mathrm{fl}(x)-x| \le \dfrac{1}{2}|x_R-x_L| \le \epsilon_u\min(|x_L|,|x_R|) < \epsilon_u|x|$$

其中第一步由舍入到最近的特性得到，第二步由 Lemma 4.23 得到.

 

Theorem 4.28. 对 $x\in\mathcal{R}(\mathcal{F})$ 有

$$\mathrm{fl}(x) = \dfrac{x}{1+\delta},\quad |\delta| \le \epsilon_u \tag{4.11}$$

$Proof.$ 类似的有

$$|\mathrm{fl}(x)-x| \le \dfrac{1}{2}|x_R-x_L| \le \epsilon_u\min(|x_L|,|x_R|) \le \epsilon_u|\mathrm{fl}(x)|$$

注意最后一步可以取等式.

 

Binary floating-point operations

Definition 4.30 (Addition/subtraction of two FPNs). 对 $a,b\in\mathcal{F},\ a = M_a\times\beta^{e_a},\ b = M_b\times \beta^{e_b},\ M_a = \pm m_a,\ M_b = \pm m_b$ ，不妨设 $|a|\ge|b|$ ，在精度至少为 $2p$ 的寄存器中计算 $c=\mathrm{fl}(a+b)\in\mathcal{F}$ .

• 比较指数
  • 若 $e_a-e_b > p+1$ ，相差超过范围，直接返回 $c=a$
  • 否则 $e_c\gets e_a,\ M_b\gets M_b/\beta^{e_a-e_b}$ ，这里对 $M_b$ 右移即可
• 加法 $M_c\gets M_a+M_b$ 并在寄存器中进行舍入，精度为 $2p$
• 正规化
  • 若 $M_c = 0$ ，返回 $0$
  • 否则移位使 $M_c\in[1,\beta)$
• 检查范围
  • 上溢 $NaN$
  • 下溢 $0$
• 舍入到精度 $p$
• 返回 $c\gets M_c\times \beta^e_c$

需要注意，由于精度为 $p$ ，舍入在第 $p$ 位小数进行；对于加法，最多错开 $p$ 位相加，然后舍入；对于减法，最多错开 $p+1$ 位相减，特殊情况为

$$1.000 \times 10^{0}-9.000 \times 10^{-5} = 1.000 - 0.00009 = 0.9999100\to 9.999 \times 10^{-1},\quad p=4$$

上面错开 $5$ 位，这是因为减法可能使得 $d_0=0$ ，然后左移一位，因而舍入在原先的第 $p+1$ 位小数进行.

 

Lemma 4.34. 对 $a,b\in\mathcal{F},\ a+b\in\mathcal{R}(\mathcal{F})$ 有

$$\mathrm{fl}(a+b) = (a+b)(1+\delta),\quad |\delta|<\epsilon_u \tag{4.12}$$

$Proof.$ 倒数第二步的舍入误差占主要地位，因为第二步舍入精度为 $2p$ ，只有在错开 $p+1$ 位时才有误差；然后由 Theorem 4.27 即证.

 

Definition 4.35 (Multiplication of two FPNs). 对 $a,b\in\mathcal{F},\ a = M_a\times\beta^{e_a},\ b = M_b\times \beta^{e_b},\ M_a = \pm m_a,\ M_b = \pm m_b$ ，在精度至少为 $2p$ 的寄存器中计算 $c = \mathrm{fl}(ab)\in\mathcal{F}$ .

• 指数求和 $e_c\gets e_a+e_b$
• 乘法 $M_c\gets M_aM_b$ 并在寄存器中进行舍入
• 正规化：移位使 $M_c\in[1,\beta)$
• 检查范围
  • 上溢 $NaN$
  • 下溢 $0$
• 舍入到精度 $p$
• 返回 $c\gets M_c\times \beta^e_c$

两个 $p$ 位精度的浮点数相乘得到 $2p$ 位小数.

 

Lemma 4.37. 对 $a,b\in\mathcal{F},\ |ab|\in\mathcal{R}(\mathcal{F})$ 有

$$\mathrm{fl}(ab) = (ab)(1+\delta),\quad |\delta|<\epsilon_u \tag{4.13}$$

$Proof.$ 只有倒数第二步的舍入误差，由 Theorem 4.27 即证.

 

Definition 4.38 (Division of two FPNs). 对 $a,b\in\mathcal{F},\ a = M_a\times\beta^{e_a},\ b = M_b\times \beta^{e_b},\ M_a = \pm m_a,\ M_b = \pm m_b$ ，在精度至少为 $2p+1$ 的寄存器中计算 $c = \mathrm{fl}(a/b)\in\mathcal{F}$ .

• 如果 $m_b=0$ ，直接返回 $NaN$ ；指数作差 $e_c\gets e_a-e_b$
• 除法 $M_c\gets M_a/M_b$ 并在寄存器中进行舍入
• 正规化：移位使 $M_c\in[1,\beta)$
• 检查范围
  • 上溢 $NaN$
  • 下溢 $0$
• 舍入到精度 $p$
• 返回 $c\gets M_c\times \beta^e_c$

 

Lemma 4.39. 对 $a,b\in\mathcal{F},\ a/b\in\mathcal{R}(\mathcal{F})$ 有

$$\mathrm{fl}\left(\dfrac{a}{b}\right) = \dfrac{a}{b}(1+\delta),\quad |\delta|<\epsilon_u \tag{4.14}$$

$Proof.$ 当 $|M_a|=|M_b|$ 时，没有误差；考虑 $|M_a|>|M_b|$ ，则由 $|M_a|,|M_b|\in[1,\beta)$ ，尽可能让商更小，有

$$\beta > \beta-\epsilon_M > \beta-2\epsilon_M,\quad \left|\dfrac{M_a}{M_b}\right| \ge \dfrac{\beta-\epsilon_M}{\beta-2\epsilon_M} > 1+\beta^{-1}\epsilon_M$$

这意味着第三步正规化不需要进行；设有 $p+k$ 精度，则舍入单位

$$\dfrac{1}{2}\beta^{1-p-k} = \dfrac{1}{2}\beta^{1-p}\beta^{1-p}\beta^{p-1-k} = \epsilon_u\epsilon_M\beta^{p-1-k}$$

令 $k=p+1$ ，则舍入单位为 $\epsilon_u\epsilon_M\beta^{-2}$ ；记第二步舍入结果为 $M_{c_1}$ ，倒数第二步舍入结果为 $M_{c_2}$ ，从而

$$\begin{aligned} M_{c_2} &= M_{c_1} + \delta_2,\quad |\delta_2| < \epsilon_u\\ &= \dfrac{M_a}{M_b} + \delta_1 + \delta_2,\quad |\delta_1|<\epsilon_u\epsilon_M\beta^{-2}\\ &= \dfrac{M_a}{M_b}(1+\delta)\\ |\delta| &= \left|\dfrac{\delta_1+\delta_2}{M_a/M_b}\right| < \dfrac{\epsilon_u(1+\epsilon_M\beta^{-2})}{1+\epsilon_M\beta^{-1}} < \epsilon_u \end{aligned}$$

考虑 $|M_a|<|M_b|$ ，则类似的有

$$\left|\dfrac{M_a}{M_b}\right| \le \dfrac{\beta-2\epsilon_M}{\beta-\epsilon_M} = 1 - \dfrac{\epsilon_M}{\beta-\epsilon_M} < 1 - \beta^{-1}\epsilon_M$$

因此第三步正规化一定会进行， $M_{c_1}$ 需要左移一位，因此

$$M_{c_1} = \dfrac{M_a}{M_b} + \delta_1,\quad |\delta_1|<\epsilon_u\epsilon_M\beta^{-2}\\ M_{c_2} = \beta M_{c_1} + \delta_2 = \beta\dfrac{M_a}{M_b}\left(1+\dfrac{\beta\delta_1+\delta_2}{\beta M_a/M_b}\right),\quad |\delta_2|<\epsilon_u$$

我们考虑分母上的部分，进行缩放则有

$$\beta\left|\dfrac{M_a}{M_b}\right| \ge \dfrac{\beta}{\beta-\epsilon_M} = 1 + \dfrac{\epsilon_M}{\beta-\epsilon_M} > 1 + \beta^{-1}\epsilon_M$$

代入得到

$$|\delta| = \left|\dfrac{\beta\delta_1+\delta_2}{\beta M_a/M_b}\right| < \dfrac{\epsilon_u\epsilon_M\beta^{-1}+\epsilon_u}{1+\beta^{-1}\epsilon_M} = \epsilon_u$$

即证.

 

Theorem 4.40 (Model of machine arithmetic). 记 $\mathcal{F}$ 为精度 $p$ 的正规 FPN 系统，则对任意运算 $\odot = +,-,\times,/$ ，我们有

$$\forall a,b\in\mathcal{F},\ a\odot b\in\mathcal{R}(\mathcal{F}),\quad \mathrm{fl}(a\odot b) = (a\odot b)(1+\delta),\quad |\delta|<\epsilon_u \tag{4.15}$$

当且仅当在 $2p+1$ 精度的寄存器中计算.

 

The propagation of rounding errors

Theorem 4.41. 若 $\forall i=0,1,\cdots,n,\ a_i\in\mathcal{F},\ a_i>0$ ，则

$$\mathrm{fl}\left(\sum_{i=0}^na_i\right) = (1+\delta_n)\sum_{i=0}^na_i \tag{4.16}$$

其中 $|\delta_n|<(1+\epsilon_u)^n-1\approx n\epsilon_u$ .

 

Theorem 4.44. 对给定的 $\mu\in\mathbb{R}^+$ 及正整数 $n\le \lfloor \frac{\ln2}{\mu}\rfloor$ ，设 $|\delta_i|\le \mu,\ i=1,2,\cdots,n$ ，则

$$1-n\mu\le \prod_{i=1}^n(1+\delta_i) \le 1+n\mu+(n\mu)^2 \tag{4.17}$$

或者等价地对 $I_n=[-\frac{1}{1+n\mu},1]$ 有

$$\exists\theta\in I_n,\quad \mathrm{s.t.}\quad \prod_{i=1}^n(1+\delta_i) = 1+\theta(n\mu+n^2\mu^2) \tag{4.18}$$

$Proof.$ 由 $|\delta_i|\le \mu,\ i=1,2,\cdots,n$ 可得

$$(1-\mu)^n \le \prod_{i=1}^n(1+\delta_i) \le (1+\mu)^n \le e^{n\mu}$$

我们将 $f(\mu) = (1-\mu)^n$ 在 $\mu=0$ 泰勒展开的拉格朗日余项有

$$(1-\mu)^n = 1-n\mu+\frac{1}{2}n(n-1)\theta^2 \ge 1-n\mu$$

从而左边不等式得证，而

$$e^{x} = 1+x+\dfrac{x^2}{2}+\dfrac{x^3}{3!} +\cdots \le 1+x+\dfrac{x^2}{2}e^x$$

令 $x=n\mu\le \ln2$ ，则有

$$e^{n\mu} \le 1+n\mu+(n\mu)^2$$

右边不等式得证；最后，由于 $\prod_{i=1}^n(1+\delta_i)$ 在连续函数 $f(\tau) = 1+\tau(1+n\mu)n\mu,\ \tau\in I_n$ 的值域中，由中值定理即证.

 

Accuracy and stability

Avoiding catastrophic cancellation

Definition 4.45. 令 $\hat{x}$ 为 $x\in\mathbb{R}$ 的逼近，则逼近精度可由绝对误差 absolute error

$$E_{abs}(\hat{x}) = |\hat{x}-x| \tag{4.18}$$

或者相对误差 relative error

$$E_{rel}(\hat{x}) = \dfrac{|\hat{x}-x|}{|x|} \tag{4.19}$$

进行度量.

 

Definition 4.46. 对于通过 $\hat{y} = \hat{f}(x)$ 逼近 $y=f(x)$ ，向前误差 forward error 是逼近 $y$ 的相对误差，向后误差 backward error 是满足 $f(\hat{x})=\hat{f}(x)$ 的用 $\hat{x}$ 逼近 $x$ 的相对误差的最小值.

Note. 关于向后误差，我们原本想要的是 $y=f(x)$ ，但必须通过 $\hat{y} = \hat{f}(x)$ 来近似，也就是说我们计算的是 $\hat{f}(x)$ ，有 $f(\hat{x}) = \hat{f}(x)$ ，即我们实际计算的是 $f$ 在 $\hat{x}$ 处的值。总的来说，可以看作我们实际上是在用 $f$ 在 $\hat{x}$ 处的值逼近 $f$ 在 $x$ 处的值，向后误差考虑的就是用于逼近的 $\hat{x}$ 关于实际的 $x$ 的相对误差。

事实上，我们不需要考虑结果的误差，只要 $\hat{x}$ 离 $x$ 足够近，也可以认为这种逼近是有效的。因为 $f(\hat{x}) = \hat{f}(x)$ ，所以我们保证了用 $\hat{f}(x)$ 逼近 $f(\hat{x})$ 是完全准确的，当 $\hat{x}$ 离 $x$ 足够近，$f(\hat{x})$ 离 $f(x)$ 也足够近， $\hat{f}(x)$ 可以看做是对 $f(x)$ 的良好逼近.

 

Definition 4.47 (Accuracy). 计算 $y=f(x)$ 的算法 $\hat{y} = \hat{f}(x)$ 是精确的 accurate 如果它的向前误差对任意的 $x$ 都很小

$$\exist c>0,\quad \mathrm{s.t.}\quad \forall x\in \mathrm{dom}(f),\ E_{rel}(\hat{f}(x)) = \left|\dfrac{\hat{f}(x)-f(x)}{f(x)}\right| \le c\epsilon_u \tag{4.20}$$

 
Note. 糟糕的消去：我们知道乘法和除法是精确的，但是加法和减法不一定是精确的；事实上，通过计算

$$\mathrm{fl}(\mathrm{fl}(x)\odot \mathrm{fl}(y)) = (1+C(x,y))(x\odot y)$$

对于乘法和除法 $C(x,y) = C$ ；而对于加法和减法 $C(x,y)\to \infty$ 当 $x+y\to 0$ .

 

Theorem 4.49 (Loss of most significant digits). 设 $x,y\in\mathcal{F},\ x>y>0$ ，且

$$\beta^{-t}\le 1-\dfrac{y}{x} \le \beta^{-s} \tag{4.21}$$

则在计算减法 $x-y$ 时最大有效数字的位数至多丢失 $t$ ，至少丢失 $s$ .

$Proof.$ 我们写成浮点格式 $x=m_x\times \beta^n,\ y=m_y\times \beta^m,\ 1\le m_x,m_y< \beta$ ，根据减法过程，首先对较小的 $y$ 进行移位

$$y = (m_y\times \beta^{m-n})\times\beta^n \Rightarrow x-y = (m_x-m_y\times \beta^{m-n})\times\beta^n$$

把相减后的有效数字记为 $m_{x-y}$ ，则m

$$m_{x-y} = m_x-m_y\times \beta^{m-n} = m_x\left(1-\dfrac{m_y\times \beta^m}{m_x\times \beta^n}\right) = m_x\left(1-\dfrac{y}{x}\right)$$

根据题中的不等式以及 $m_x$ 的条件有

$$\beta^{-t}\le m_{x-y} < \beta^{1-s}$$

因此进行正规化时，要左移至多 $t$ 位，至少 $s$ 位.

 

Note. 当 $x,y$ 是两个非常接近的数时，进行减法操作就会出现上面的问题，因此要尽量避免这种情况出现.

 

Backward stability and numerical stability

Definition 4.52 (Backward stability). 计算 $y=f(x)$ 的算法 $\hat{y} = \hat{f}(x)$ 是向后稳定的 backward stable 若

$$\exist c>0,\quad \mathrm{s.t.}\quad \forall x\in \mathrm{dom}(f),\ \exists\hat{x}\in\mathrm{dom}(f),\quad \mathrm{s.t.}\quad \hat{f}(x)=f(\hat{x})\ \Rightarrow\ E_{rel}(\hat{x}) \le c\epsilon_u \tag{4.20}$$

Definition 4.53. 计算 $y=f(x_1,x_2)$ 的算法 $\hat{y} = \hat{f}(x_1,x_2)$ 是向后稳定的 backward stable 若

$$\exist c_1,c_2>0,\quad \mathrm{s.t.}\quad \forall (x_1,x_2)\in \mathrm{dom}(f),\ \exists(\hat{x}_1,\hat{x}_2)\in\mathrm{dom}(f),\quad \mathrm{s.t.}\\ \hat{f}(x_1,x_2)=f(\hat{x}_1,\hat{x}_2)\ \Rightarrow\ E_{rel}(\hat{x}_1) \le c_1\epsilon_u,\ E_{rel}(\hat{x}_2) \le c_2\epsilon_u \tag{4.21}$$

也就是说对任何 $x$ 的向后误差都足够小.

 

Lemma 4.54. 对 $f(x_1,x_2) = x_1-x_2,\ x_1,x_2\in\mathcal{R}(\mathcal{F})$ ，则算法 $\hat{f}(x_1,x_2) = \mathrm{fl}(\mathrm{fl}(x_1)- \mathrm{fl}(x_2))$ 是向后稳定的.

$Proof.$ 直接计算

$$\hat{f}(x_1,x_2) = (x_1(1+\delta_1)-x_2(1+\delta_2))(1+\delta_3) = x_1(1+\delta_1+\delta_3+\delta_1\delta_3)-x_2(1+\delta_2+\delta_3+\delta_2\delta_3)$$

因此分别有

$$\hat{x}_1 = (1+\delta_1+\delta_3+\delta_1\delta_3)x_1,\quad \hat{x}_2 = (1+\delta_2+\delta_3+\delta_2\delta_3)x_2$$

从而向后稳定.

 

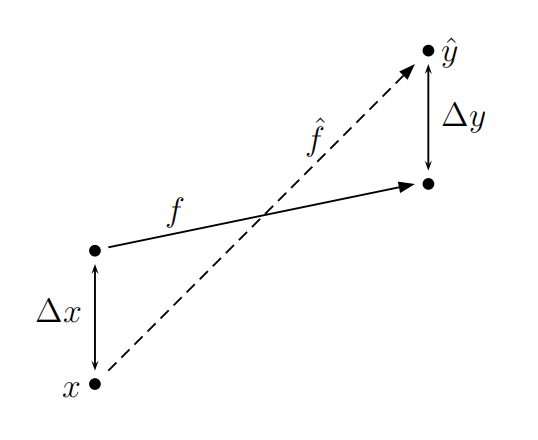
Definition 4.56. 计算 $y=f(x)$ 的算法 $\hat{y} = \hat{f}(x)$ 是稳定的 stable 或数值稳定 numerically stable 当且仅当

$$\exist c,c_f>0,\quad \mathrm{s.t.}\quad \forall x\in \mathrm{dom}(f),\ \exists\hat{x}\in\mathrm{dom}(f),\quad \mathrm{s.t.}\quad \left|\dfrac{\hat{f}(x)-f(\hat{x})}{f(\hat{x})}\right| \le c_f\epsilon_u,\ E_{rel}(\hat{x}) \le c\epsilon_u \tag{4.22}$$

注意这里第一个条件是关于 $f(\hat{x})$ 的相对误差，第二个条件是关于 $\hat{x}$ 的相对误差.

 

Lemma 4.57. 如果一个算法向后稳定，则它是数值稳定的.

$Proof.$ 由向后稳定，有 $\hat{f}(x)=f(\hat{x})$ ，故第一个条件显然；第二个条件显然成立.

 

Condition numbers: scalar functions

Definition 4.59. 函数 $y=f(x)$ 的相对条件数 condition number 是输入的微小变化对输出的相对变化的度量

$$C_f(x) = \left|\dfrac{xf^{\prime}(x)}{f(x)}\right| \tag{4.23}$$

Definition 4.60. 条件数小的问题称为是良态的 well-conditioned 否则称为是病态的 ill-conditioned .

 

Lemma 4.63. 考虑在单根 $r$ 附近求解 $f(x)=0$ ，即有 $f(r)=0,\ f^{\prime}(r)\neq 0$ ，设有微小扰动 $F=f+\epsilon g,\ f,g\in\mathcal{C}^2,\ g(r)\neq 0$ 且满足 $|\epsilon g^{\prime}(r)|\ll |f^{\prime}(r)|$ ，则 $F$ 有根 $r+h$ ，其中

$$h\approx -\epsilon\dfrac{g(r)}{f^{\prime}(r)} \tag{4.24}$$

$Proof.$ 直接泰勒展开

$$0 = F(r+h) = f(r) + hf^{\prime}(r) + \epsilon [g(r)+hg^{\prime}(r)] + O(h^2)$$

从而有

$$h\approx -\epsilon\dfrac{g(r)}{f^{\prime}(r)+\epsilon g^{\prime}(r)} \approx -\epsilon\dfrac{g(r)}{f^{\prime}(r)}$$

即证.

 

Example 4.64 (Wilkinson). 定义

$$f(x) = \prod_{k=1}^p(x-k),\quad g(x) = x^p$$

考虑根 $x=p$ 受到扰动 $f+\epsilon g$ 后的影响.

由上面的引理，我们有

$$h\approx -\epsilon\dfrac{g(r)}{f^{\prime}(r)} = -\epsilon \dfrac{p^p}{(p-1)!}$$

当 $p$ 很大时，扰动越来越大，因此求解高阶多项式的根几乎不可能.

 

Condition numbers: vector functions

Definition 4.65. 向量函数 $\mathbf{f}:\mathbb{R}^m\to\mathbb{R}^n$ 的条件数为

$$\mathrm{cond}_{\mathbf{f}}(\mathbf{x}) = \dfrac{\|\mathbf{x}\|\|\nabla\mathbf{f}\|}{\|\mathbf{f}(\mathbf{x})\|} \tag{4.25}$$

其中 $\|\cdot\|$ 表示欧几里得范数.

 

Definition 4.68. 向量函数 $\mathbf{f}:\mathbb{R}^m\to\mathbb{R}^n$ 的分量条件数 component wise condition number 为

$$\mathrm{cond}_{\mathbf{f}}(\mathbf{x}) = \|A(\mathbf{x})\| \tag{4.26}$$

其中矩阵 $A(\mathbf{x}) = [a_{ij}(\mathbf{x})]$ ，每一个部分为

$$a_{ij}(\mathbf{x}) = \left|\dfrac{x_j\frac{\partial f_i}{\partial x_j}}{f_i(\mathbf{x})}\right| \tag{4.27}$$

也就是说 $a_{ij}$ 是 $f_i(\mathbf{x})$ 关于 $x_j$ 的条件数.

 

Definition 4.70. 希尔伯特矩阵 Hilbert matrix $H_n\in\mathbb{R}^{n\times n}$ 是

$$h_{i,j} = \dfrac{1}{i+j-1} \tag{4.28}$$

 
Definition 4.72. 范德蒙德矩阵 Vandermonde matrix $V_n\in\mathbb{R}^{n\times n}$ 是

$$v_{i,j} = t_j^{i-1} \tag{4.29}$$

其中 $t_1,\cdots,t_n$ 是参数.

 

Condition numbers: algorithms

Definition 4.74. 向量函数 $\mathbf{f}:\mathbb{R}^m\to\mathbb{R}^n$ 通过算法 $\mathbf{f}_A:\mathcal{F}^m\to\mathcal{F}^n$ 逼近，设

$$\forall \mathbf{x}\in\mathcal{F}^m,\ \exist\mathbf{x}_A\in\mathbb{R}^m,\quad \mathrm{s.t.}\quad \mathbf{f}_A(\mathbf{x}) = \mathbf{f}(\mathbf{x}_A) \tag{4.30}$$

则算法 $\mathbf{f}_A$ 的条件数定义为

$$\mathrm{cond_A(\mathbf{x})} = \dfrac{1}{\epsilon_u}\inf_{\{\mathbf{x}_A\}}\dfrac{\|\mathbf{x}_A-\mathbf{x}\|}{\|\mathbf{x}\|} \tag{4.31}$$

也就是向后误差的下确界.

 

Theorem 4.76. 设光滑函数 $f:\mathbb{R}\to\mathbb{R}$ 由算法 $A:\mathcal{F}\to\mathcal{F},\ f_A(x) = f(x)(1+\delta(x)),\ |\delta(x)|\le\varphi(x)\epsilon_u$ 逼近，若 $\mathrm{cond}_f(x)$ 有界非零，则有

$$\forall x\in\mathcal{F},\quad \mathrm{cond}_A(x)\le \dfrac{\varphi(x)}{\mathrm{cond}_f(x)} \tag{4.32}$$

$Proof.$ 设有 $x_A$ 满足 $f(x_A)=f_A(x)$ ，将 $x_A$ 写作 $x(1+\epsilon_A)$ ，则

$$f(x)(1+\delta) = f(x_A) = f(x(1+\epsilon_A)) = f(x) + x\epsilon_Af^{\prime}(x) + O(\epsilon_A^2)\ \Rightarrow\ \epsilon_A = \dfrac{f(x)}{xf^{\prime}(x)}\delta$$

计算相对误差

$$\left|\dfrac{x_A-x}{x}\right| = |\epsilon_A| = \left|\dfrac{f(x)}{xf^{\prime}(x)}\right||\delta(x)|\ \Rightarrow\ \dfrac{1}{\epsilon_u}\left|\dfrac{x_A-x}{x}\right| = \left|\dfrac{\delta(x)}{\epsilon_u\mathrm{cond}_f(x)}\right| \le \dfrac{\varphi(x)}{\mathrm{cond}_f(x)}$$

对 $x_A$ 取下确界， $x$ 取上确界即证.

 

Overall error of a computer solution

Theorem 4.79. 考虑正规 FPN 求解数学问题

$$\mathbf{f}:\mathbb{R}^m\to\mathbb{R}^n,\quad \mathbf{y} = \mathbf{f}(\mathbf{x}) \tag{4.33}$$

将计算机的输入输出表示为

$$\mathbf{x}^*\approx \mathbf{x},\quad \mathbf{y}^*_A = \mathbf{f}_A(\mathbf{x}^*) \tag{4.34}$$

其中 $\mathbf{f}_A$ 是逼近 $\mathbf{f}$ 的算法，则逼近 $\mathbf{y}$ 与 $\mathbf{y}^*$ 的相对误差有界

$$E_{rel}(\mathbf{y}^*_A) \lessapprox E_{rel}(\mathbf{x}^*_A)\mathrm{cond}_{\mathbf{f}}(\mathbf{x}) + \epsilon_u\mathrm{cond}_{\mathbf{f}}(\mathbf{x}^*)\mathrm{cond}_{A}(\mathbf{x}^*) \tag{4.35}$$

$Proof.$ 证明省略.

 

Problem

$\mathrm{III}.$ 令 $x=\beta^e,\ e\in\mathbb{Z},\ L<e<U$ 为正规 FPN ，而 $x_L,x_R$ 为两个相邻的正规 FPN 满足 $x_L<x<x_R$ ，则 $x_R-x=\beta(x-x_L)$ .

$Proof.$ 由 $x = 1 \times \beta^e$ ，则有 $x_R = (1 + 1 \times \beta^{1-p}) \times \beta^e$ ，从而 $x_R - x = \beta^{1-p} \times \beta^e = \beta^{e+1-p}$ ，而

$$x_L = (\beta - 1) \times (1 + \beta^{-1} + \beta^{-2} + \cdots + \beta^{1-p}) \times \beta^{e-1}$$

从而有

$$\begin{aligned} x - x_L &= (\beta - (\beta - 1) \times (1 + \beta^{-1} + \beta^{-2} + \cdots + \beta^{1-p})) \times \beta^{e-1}\\ &= \left(\beta - (\beta - 1) \times \dfrac{1-\beta^{-p}}{1-\beta^{-1}}\right) \times \beta^{e-1}\\ &= (\beta - (1-\beta^{-p}) \times \beta) \times \beta^{e-1}\\ &= \beta^{e-p} \end{aligned}$$

故 $x_R - x = \beta(x - x_L)$ .

 

$\mathrm{IV}.$ 在 IEEE 754 单精度下进行舍入.

$$\begin{aligned} \dfrac{3}{5} = (1.00110011\cdots)_2 \times 2^{-1}\\ x_L = (1.0011\cdots001)_2 \times 2^{-1}\\ x_R = (1.0011\cdots010)_2 \times 2^{-1} \end{aligned}$$

且有

$$\begin{aligned} x - x_L &= \dfrac{3}{5} \times 2^{-24}\\ x_R - x_L &= 2^{-24}\\ x_R - x &= (x_R - x_L) - (x - x_L) = \dfrac{2}{5} \times 2^{-24} \end{aligned}$$

故 $\mathrm{fl}(x) = x_R = (1.0011\cdots010)_2 \times 2^{-1}$ ，

$$\left|\dfrac{x_R-x}{x}\right| = \dfrac{2}{3} \times 2^{-24}$$

注意舍入精度为 $24$ ，即保留到小数点后 $23$ 位.

 

$\mathrm{V}.$ 如果 IEEE 754 单精度不再舍入到最近，而是直接截断，求单位舍入.

机器精度 $\epsilon_M = 2^{-23}$ ，由于直接截断，则舍入的最大相对误差

$$\epsilon_u = \max\left|\dfrac{\mathrm{fl}(x)-x}{x}\right| < \max\left|\dfrac{2^{-23}}{x}\right| = 2^{-23}$$

从而 $\epsilon_u = 2^{-23}$ .

 

$\mathrm{VI}.$ 在计算 $1-\cos \frac{1}{4}$ 的精度损失.

根据定理 Theorem 4.49 我们计算

$$1-\dfrac{y}{x} = 1 - \dfrac{\cos \frac{1}{4}}{1} = 1-\cos \frac{1}{4}$$

有范围

$$0.015625 = 2^{-6} < 1 - \cos\frac{1}{4} < 2^{-5} = 0.03125$$

故精度损失 $6$ 位.

 

$\mathrm{VII}.$ 两种避免 $1-\cos x$ 的精度损失的方法.

• 计算泰勒展开

$$\begin{aligned} 1 - \cos x &= 1 - \left(1 - \dfrac{x^2}{2} + \dfrac{x^4}{4!} - \dfrac{x^6}{6!} \cdots \right)\\ &= \dfrac{x^2}{2} - \dfrac{x^4}{4!} + \dfrac{x^6}{6!} - \cdots \end{aligned}$$

• 计算

$$1 - \cos x = \dfrac{1 - \cos^{2}x}{1 + \cos x} = \dfrac{\sin^{2}x}{1 + \cos x}$$

用多个乘除法替代.

 

$\mathrm{IX}.$ 算法 $A$ 估计 $f(x)=1-e^{-x}$ ，其中指数函数的相对误差为机器精度，对 $[0,1]$ 估计 $\mathrm{cond}_A(x)$ .

利用估计

$$\forall x\in\mathcal{F},\quad \mathrm{cond}_A(x)\le \dfrac{\varphi(x)}{\mathrm{cond}_f(x)}$$

不妨假设估计为 $f_A(x)$ ，在计算时忽略 $\delta_i\delta_i$ ，则有

$$\begin{aligned} f_A(x) &= (1-e^{-x}(1+\delta_1))(1+\delta_2)\\ &= 1 + \delta_2 - e^{-x}(1+\delta_1+\delta_2 + \delta_1\delta_2)\\ &\approx f(x)\left(1+\dfrac{\delta_2-e^{-x}(\delta_1+\delta_2)}{1-e^{-x}}\right)\\ &= f(x)(1+\delta(x)) \end{aligned}$$

考虑 $|\delta(x)|<\epsilon_u\varphi(x)$ ，从而有

$$\varphi(x) = \dfrac{1-2e^{-x}}{1-e^{-x}},\quad \mathrm{cond}_f(x) = \left|\dfrac{xf^{\prime}(x)}{f(x)}\right| = \dfrac{x}{e^x-1}$$

其中 $\mathrm{cond}_f(x)$ 有界非零，代入估计式

$$\mathrm{cond}_A(x) \le \dfrac{e^x-2}{x}$$

从而在 $x=0$ 附近算法条件数趋于无穷.

 

$\mathrm{X}.$ 寻找多项式的根

$$q(x) = \sum_{i=0}^na_ix^i,\quad a_n=1,\ a_0\neq 0,\ a_i\in\mathbb{R}$$

可以考虑向量函数 $f:\mathbb{R}^n\to\mathbb{C}$

$$r=f(a_0,a_1,\cdots,a_{n-1})$$

推导 $f$ 基于 $1$ 范数的分量条件数.

令 $\mathbf{a} = (a_0,a_1,\cdots,a_{n-1})^{T}$ ，根据 $q(x)$ 得到的函数 $f$ 为

$$f(\mathbf{a}) = \sum_{i=0}^{n}a_ix^i$$

条件矩阵 $A(\mathbf{a})$ 是 $1\times n$ 矩阵

$$A(\mathbf{a}) = \dfrac{1}{|f(\mathbf{a})|}\left(|a_0|, |a_1x|, \cdots, \left|a_{n-1}x^{n-1}\right|\right)$$

从而有

$$\begin{aligned} \mathrm{cond}_f(\mathbf{a}) &= \dfrac{1}{|f(\mathbf{a})|}\left\|\left(|a_0|, |a_1x|, \cdots, \left|a_{n-1}x^{n-1}\right|\right)\right\|_1\\ &= \dfrac{\max\left(|a_0|, |a_1x|, \cdots, \left|a_{n-1}x^{n-1}\right|\right)}{\left|\sum_{i=0}^{n}a_ix^i\right|} \end{aligned}$$

对于 Wilkinson 情况，

$$f(x) = \prod_{k=1}^p(x-k) = x^p + \sum_{i=0}^{p-1}b_ix^i,\quad g(x) = x^p$$

则求 $f+\epsilon g$ 的根等价于

$$f+\epsilon g= x^p + \sum_{i=0}^{p-1}b_ix^i + \epsilon x^{p} = 0\ \Leftrightarrow\ x^p + \sum_{i=0}^{p-1}c_ix^i = 0,\ c_i = \dfrac{b_i}{1+\epsilon}$$

也就是说，求解 $f+\epsilon g$ 的根实际上相当于对 $f$ 的系数做出相对扰动

$$\dfrac{\left|c_i-b_i\right|}{|b_i|} = \dfrac{\epsilon}{1+\epsilon}$$

得到的首一多项式求根，应用之前首一多项式系数的条件数公式，它在 $x=p$ 附近条件数趋于无穷，因此系数受到的扰动很大，它的根受到的扰动也很大.

 

$\mathrm{XII}.$ 在 IEEE 754 单精度 FPN 中，对区间 $[128,129]$ 应用二分法，则绝对精度能否 $<10^{-6}$ ？

要满足 $|x-x^*| < 10^{-6}$ ，但有整数部分 $128 = 2^7$ ，而

$$2^{-20} < 1 \times 10^{-6} < 2^{-19}$$

从而整数部分 $8$ 位，小数部分 $19$ 位，正规化后需要至少 $27$ 位，因此不能达到要求.