裁剪算法

目录

• 直线段裁剪
  • Cohen-Sutherland 裁剪
  • 中点分割裁剪
  • 梁友栋 -Barskey 算法
• 多边形裁剪

 

在使用计算机处理图形信息时，计算机内部存储的图形往往比较大，而屏幕显示的只是图形的一部分。因此需要确定图形中哪些部分落在显示区之内，哪些落在显示区之外，一般只显示落在显示区内部的图形，这个选择过程称为裁剪。

 

直线段裁剪

任意一条直线段与窗口之间只有以下四种情况

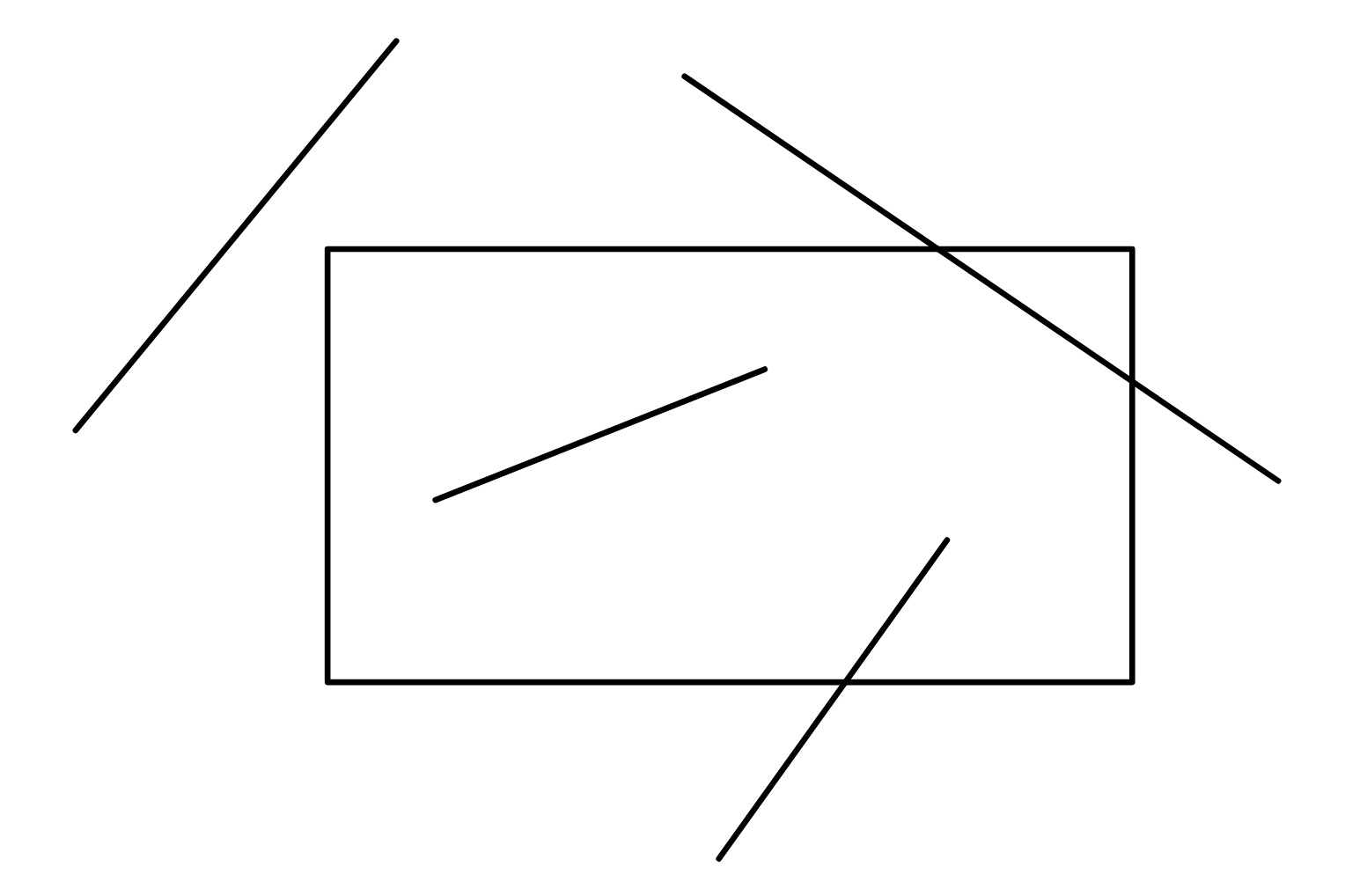
我们通过位运算编码来判断线段与窗口之间的位置关系：对于上下左右四种情况分四位编码

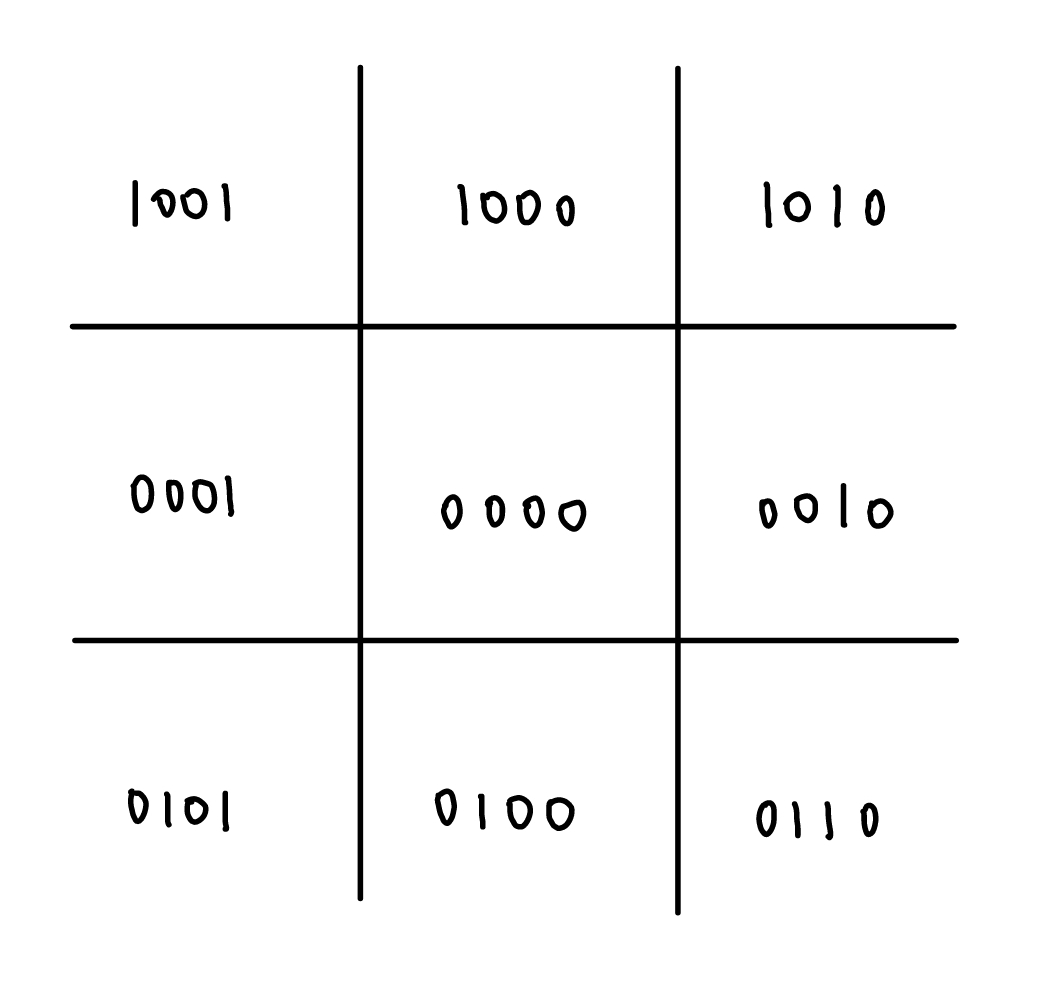
如图各位分别表示表示在窗口上方、下方、右方、左方，只要满足位置关系，该位就设为 1 ，否则为 0 。

 

Cohen-Sutherland 裁剪

该算法的思想就是利用上面的编码，先将在窗口内和在窗口外的简单情况处理掉，然后对有交点的情况计算交点。

对于有交点的情况：

1. 选择在窗口外的端点
2. 根据此端点与窗口的位置关系，利用线段表达式 \(y=y_0+k(x-x_0)\) 计算交点
3. 用交点替换此端点来实现裁剪

不断循环直到端点均在窗口内，这样就得到裁剪后的线段。

 

中点分割裁剪

此算法使用类似于前的端点编码，但是对于有交点的情况，使用中点分割的方式分别计算交点

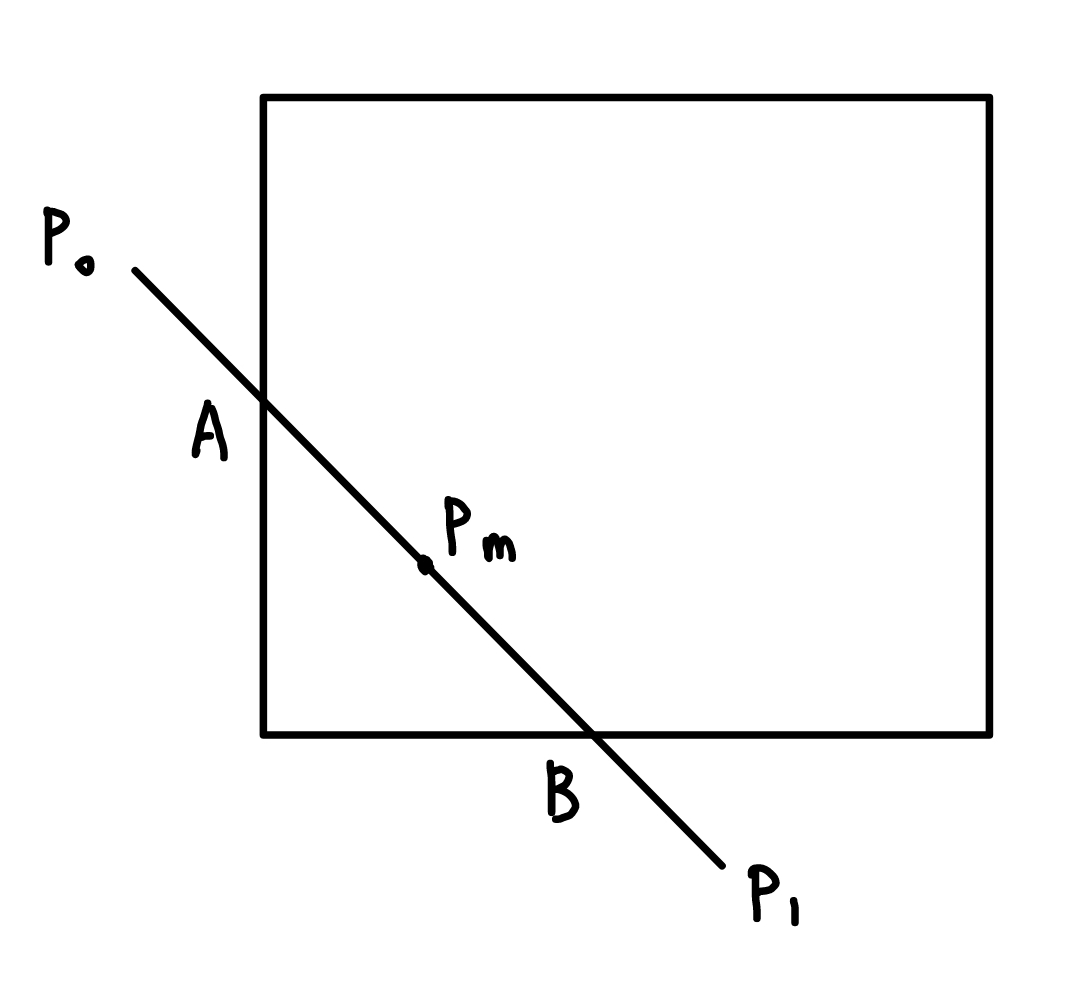
本质上是一种二分法，如上图中分别在 \(P_0P_m,\ P_mP_1\) 两段上再取中点，选择有交点的部分重复操作，直到线段长度足够小时停止。这种裁剪方式的好处在于它只需要加法和除以 2 ，便于硬件实现。

 

代码实现

#define LEFT 1
#define RIGHT 2
#define BOTTOM 4
#define TOP 8

// 裁剪区域
RECT area = {100, 100, 300, 300};

// 根据区域编码
int encode(POINT &p)
{
    int c = 0;
    if (p.x < area.left)
    {
        c |= LEFT;
    }
    if (p.x > area.right)
    {
        c |= RIGHT;
    }
    if (p.y < area.top)
    {
        c |= TOP;
    }
    if (p.y > area.bottom)
    {
        c |= BOTTOM;
    }
    return c;
}

POINT midPoint(POINT &p1, POINT &p2)
{
    return {(p1.x + p2.x) / 2, (p1.y + p2.y) / 2};
}

// 取中点搜索交点
POINT midFind(POINT &p1, POINT &p2)
{
    int code[2], ind = 0;

    // 记录位置
    code[0] = encode(p1);
    code[1] = encode(p2);

    POINT points[2] = {p1, p2};

    // 当两个点相差很小才退出
    while (abs(points[0].x - points[1].x) > 1 || abs(points[0].y - points[1].y) > 1)
    {
        // 当第一个点在区域中，就选择这个点
        ind = (code[0] == 0) ? 0 : 1;
        // points[ind] 在内部

        // 取中点
        POINT pm = midPoint(points[0], points[1]);
        int codem = encode(pm);

        // 如果中点在区域中，选择 pm 替代
        if (codem == 0)
        {
            points[ind] = pm;
            code[ind] = codem;
        }
        else
        {
            points[1 - ind] = pm;
            code[1 - ind] = codem;
        }
    }
    return points[ind];
}

void cutLine(HDC hdc, POINT *points)
{
    int code[2], codem;

    code[0] = encode(points[0]);
    code[1] = encode(points[1]);

    // 两点在区域同侧，舍弃
    if ((code[0] & code[1]) != 0)
    {
        return;
    }

    // 有交点
    if (code[0] != 0 || code[1] != 0)
    {
        int ind = (code[0] == 0) ? 0 : 1;

        // 如果有一个为 0 ，直接寻找交点
        if (code[ind] == 0)
        {
            points[1 - ind] = midFind(points[0], points[1]);
        }
        else
        {
            // 取中点
            POINT pm = midPoint(points[0], points[1]);

            // 如果不在区域内就裁剪
            while ((codem = encode(pm)) != 0)
            {
                // 如果在同侧，就用中点替代
                if ((code[0] & codem) != 0)
                {
                    points[0] = pm;
                    code[0] = codem;
                }
                else
                {
                    points[1] = pm;
                    code[1] = codem;
                }
                pm = midPoint(points[0], points[1]);
            }

            // 分两段搜索交点
            points[0] = midFind(points[0], pm);
            points[1] = midFind(pm, points[1]);
        }
    }

    Polyline(hdc, points, 2);
}

 

绘图测试程序：

case WM_PAINT:
{
    PAINTSTRUCT ps;
    HDC hdc = BeginPaint(hWnd, &ps);
    // TODO: 在此处添加使用 hdc 的任何绘图代码...
    Rectangle(hdc, area.left, area.top, area.right, area.bottom);

    HPEN mPen = CreatePen(PS_SOLID, 1, RGB(255, 0, 0));

    POINT points[2] = {{50, 200}, {150, 250}};
    POINT points1[2] = {{20, 200}, {350, 250}};

    HPEN oldPen = (HPEN)SelectObject(hdc, mPen);

    // 裁剪前的图像
    Polyline(hdc, points, 2);
    Polyline(hdc, points1, 2);

    SelectObject(hdc, oldPen);
    DeleteObject(mPen);

    // 裁剪后的图像
    cutLine(hdc, points);
    cutLine(hdc, points1);

    EndPaint(hWnd, &ps);
}

 

梁友栋 -Barskey 算法

梁友栋和 Barskey 提出了更快的参数化裁剪算法，首先写出裁剪条件

\[x_l \le x_1+u\Delta x \le x_r\\ y_b \le y_1+u\Delta y \le y_t \]

下标 \(l,r,t,b\) 分别表示左右上下。这四个不等式可以表示为形式 \(up_k\le q_k\) ，其中

\[\left\{ \begin{aligned} p_1 &= -\Delta x\\ q_1 &= x_1-x_l \end{aligned} \right. \quad \left\{ \begin{aligned} p_2 &= \Delta x\\ q_2 &= x_r-x_1 \end{aligned} \right. \quad \left\{ \begin{aligned} p_3 &= -\Delta y\\ q_3 &= y_1-y_b \end{aligned} \right. \quad \left\{ \begin{aligned} p_4 &= \Delta y\\ q_4 &= y_t-y_1 \end{aligned} \right. \]

于是对每条直线都可以计算出 \(u_1,u_2\) ，它们定义了在窗口内的线段部分。

 

多边形裁剪

显然我们希望多边形裁剪的结果仍然是多边形，但如果还使用线段的裁剪方式，很可能得到的是一系列无法封闭的线段。当多边形作为实区域考虑时，为了方便填充，我们也应当使裁剪结果封闭。

 

Sutherland-Hodgeman 算法的基本思想是一次用窗口的一条边裁剪多边形。先考虑窗口的一条边的延长线，我们用这条延长线来裁剪多边形的点。按照顺序考虑多边形边的端点，有如下四种情况：

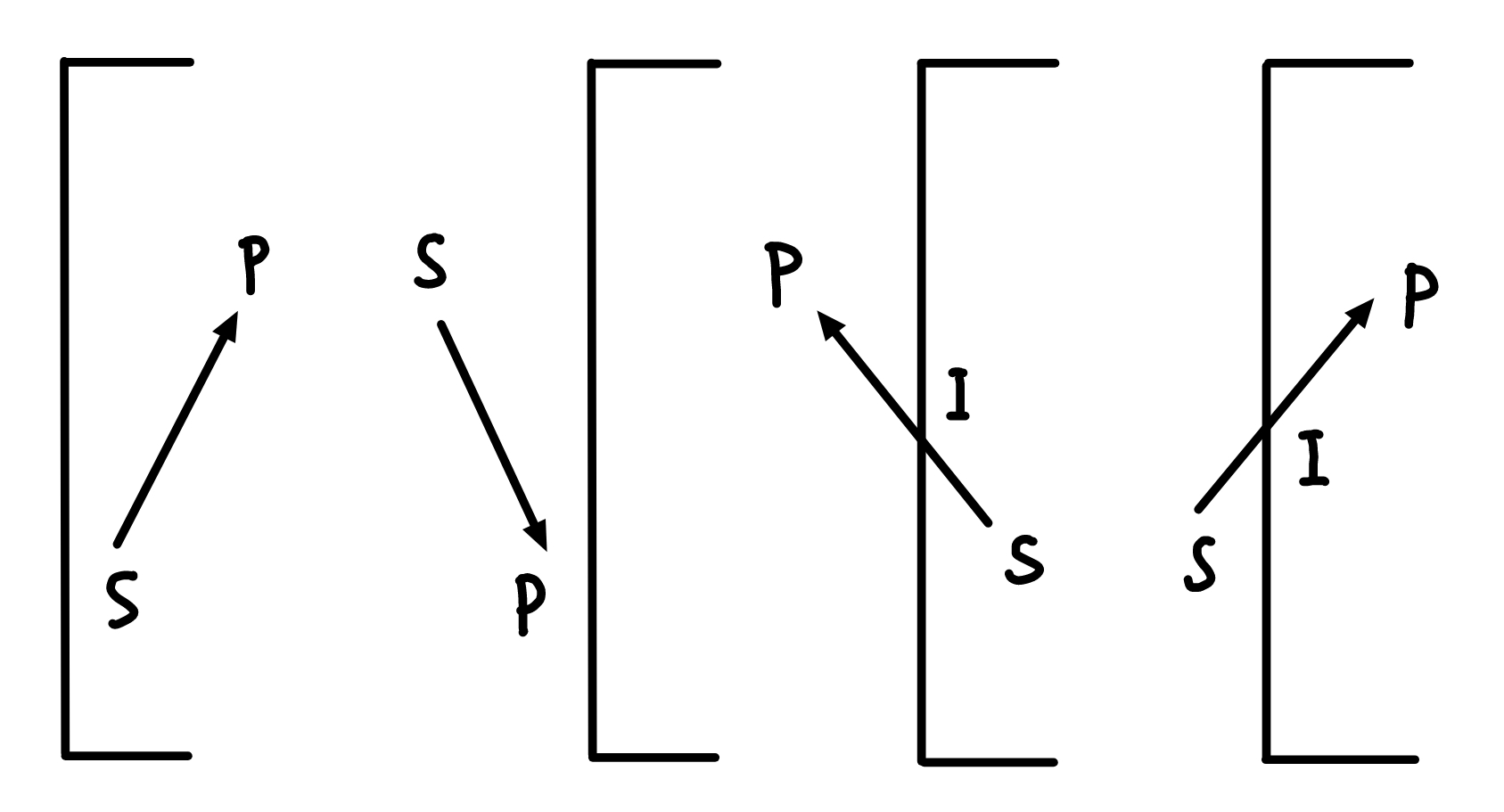
其中箭头方向表示读取端点的顺序，对于情况 1 返回 \(P\) ，情况 2 不返回，情况 3 返回 \(S,I\) ，情况 4 返回 \(I,P\) ，也就是说我们对每条边都返回有效的顶点，最后得到的顶点集就构成了封闭图形。

 

代码实现

#define MAX_SIZE 128

// 裁剪区域
RECT boundary = { 400, 100, 600, 300 };

typedef POINT Edge[2];
typedef POINT Vertex[MAX_SIZE];

// 判断点是否在裁剪框内部，裁剪边的点按照逆时针顺序排布
bool inside(POINT &p, Edge ClipBoundary)
{
    // 裁剪边是下边
    if (ClipBoundary[0].x < ClipBoundary[1].x)
    {
        if (p.y <= ClipBoundary[0].y)
        {
            return true;
        }
    }
    // 裁剪边是上边
    else if (ClipBoundary[0].x > ClipBoundary[1].x)
    {
        if (p.y >= ClipBoundary[0].y)
        {
            return true;
        }
    }
    // 裁剪边是右边
    else if (ClipBoundary[0].y > ClipBoundary[1].y)
    {
        if (p.x <= ClipBoundary[0].x)
        {
            return true;
        }
    }
    // 裁剪边是左边
    else if (ClipBoundary[0].y < ClipBoundary[1].y)
    {
        if (p.x >= ClipBoundary[0].x)
        {
            return true;
        }
    }
    return false;
}

// 直线段 SP 与窗口边界求交，返回交点 I
void intersect(POINT &S, POINT &P, Edge ClipBoundary, POINT &I)
{
    // 裁剪边水平
    if (ClipBoundary[0].y == ClipBoundary[1].y)
    {
        I.y = ClipBoundary[0].y;
        I.x = S.x + 1.0 * (ClipBoundary[0].y - S.y) * (P.x - S.x) / (P.y - S.y);
    }
    // 否则是竖直
    else
    {
        I.x = ClipBoundary[0].x;
        I.y = S.y + 1.0 * (ClipBoundary[0].x - S.x) * (P.y - S.y) / (P.x - S.x);
    }
}

// 将点输出
void output(POINT &p, int &outLength, Vertex outPoints)
{
    outPoints[outLength] = p;
    outLength++;
}

// 单边 ClipBoundary 裁剪
void oneBoundaryClip(Vertex inPoints, Vertex outPoints, Edge ClipBoundary, int &inLength, int &outLength)
{
    POINT S, P, ip;
    S = inPoints[inLength - 1];
    outLength = 0; // 输出点的个数

    for (int i = 0; i < inLength; i++)
    {
        P = inPoints[i];
        if (inside(P, ClipBoundary))
        {
            // 两个点都在裁剪框中，输出 P
            if (inside(S, ClipBoundary))
            {
                output(P, outLength, outPoints);
            }
            // 否则裁剪
            else
            {
                intersect(S, P, ClipBoundary, ip);
                output(ip, outLength, outPoints);
                output(P, outLength, outPoints);
            }
        }
        else if (inside(S, ClipBoundary))
        {
            // S 在窗口内， P 在窗口外
            intersect(S, P, ClipBoundary, ip);
            output(ip, outLength, outPoints);
        }
        // 两个点都不在窗口中不需要处理
        S = P;
    }
}

// 复制顶点
void copyVertex(Vertex v1, Vertex v2, int size)
{
    for (int i = 0; i < size; i++)
    {
        v1[i] = v2[i];
    }
}

// 完整裁剪过程
void SutherlandHodgemanClip(HDC hdc, Vertex inPoints, int n)
{
    // 4 条裁剪边
    Edge boundaryList[4] = {{boundary.left, boundary.top, boundary.left, boundary.bottom},
                            {boundary.right, boundary.top, boundary.left, boundary.top},
                            {boundary.right, boundary.bottom, boundary.right, boundary.top},
                            {boundary.left, boundary.bottom, boundary.right, boundary.bottom}};

    // 作为输出的容器
    Vertex outPoints;
    int inLength = n;
    int outLength;

    // 依次裁剪 4 个边
    for (int i = 0; i < 4; i++)
    {
        oneBoundaryClip(inPoints, outPoints, boundaryList[i], inLength, outLength);
        copyVertex(inPoints, outPoints, outLength);
        inLength = outLength;
    }

    Polygon(hdc, inPoints, inLength);
}

 

绘图测试程序：

case WM_PAINT:
{
    PAINTSTRUCT ps;
    HDC hdc = BeginPaint(hWnd, &ps);
    // TODO: 在此处添加使用 hdc 的任何绘图代码...
    Rectangle(hdc, boundary.left, boundary.top, boundary.right, boundary.bottom);

    Vertex points2 = {{380, 260}, {450, 320}, {630, 150}, {610, 120}};

    HPEN mPen = CreatePen(PS_SOLID, 1, RGB(255, 0, 0));
    HPEN oldPen = (HPEN)SelectObject(hdc, mPen);

    // 裁剪前的图像
    Polygon(hdc, points2, 4);

    SelectObject(hdc, oldPen);
    DeleteObject(mPen);

    // 裁剪后的图像
    SutherlandHodgemanClip(hdc, points2, 4);

    EndPaint(hWnd, &ps);
}