重要性采样和蒙特卡洛方法
蒙特卡洛积分
在工程任务中，往往会出现无法求出定积分的精确值的情况，这时就需要使用数值积分方法进行求解。
对定义在 \([a,b]\) 上的函数 \(f(x)\) 的积分 \(\int_a^bf(x)dx\) ，蒙特卡洛积分通过选取采样点 \(\{x_1,\cdots,x_n\}\) 对应的函数值进行求和来近似定积分。例如对于均匀采样，估计式为
\[\int_a^bf(x)dx = \dfrac{b-a}{n}\sum_{i=1}^nf(x_i)
\]
这种估计的精度取决于采样点的个数和分布，我们需要用尽可能少的取样点，调整到合适的分布来提高近似精度。
重要性采样
不妨假设被积函数非负，这样其定积分就是与 \(x\) 轴围成的面积 \(S\) ，我们用端点代替区间，记 \(\Delta_i\) 处的面积为 \(S_i\) ，那么可以考虑
\[p(\Delta_i) = \dfrac{S_i}{S},\quad \int_a^bf(x)dx = \dfrac{1}{n}\sum_{i=1}^n\dfrac{S_i}{p(\Delta_i)}
\]
其中 \(p(\Delta_i)\) 表示端点处的面积密度；需要注意 \(p(\Delta_i)\) 不是概率而是密度，则
\[\int_{\Delta_i}^{\Delta_{i+1}}f(\Delta_i)dx = S\int_{\Delta_i}^{\Delta_{i+1}}p(\Delta_i)dx
\]
即此处的定积分是密度函数积分后得到的概率乘上总面积，因此 \(S_i=f(\Delta_i)\) ，但这种局部估计往往并不精确，因此我们在每一段区间上估计 \(S\) ，然后取平均值来近似。
我们并不知道概率密度函数 \(p\) ，实际上通常需要根据 \(f(x)\) 的 “形状” 来取定。如果取均匀分布，上述估计式就变为先前的均匀采样估计式；由于近似受到函数值大小的影响：函数值越大，影响越大。因此需要在函数值大的部分赋予更大的概率密度，例如
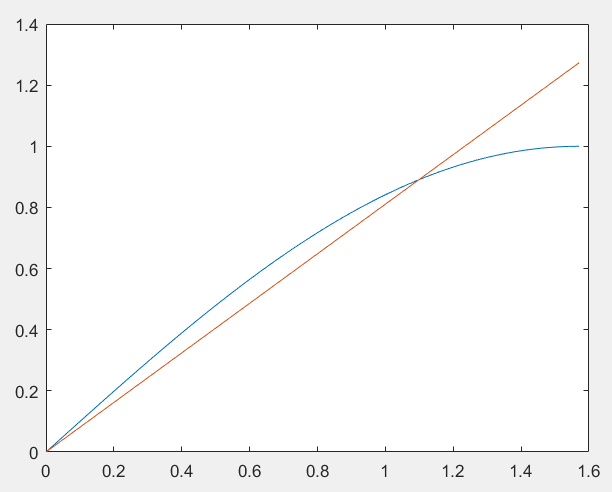
\[f(x) = \sin x,\quad x\in\left[0,\dfrac{\pi}{2}\right],\quad p(x) = \dfrac{8x}{\pi^2}
\]
两个函数在此区间上具有类似的增长关系
最后我们给出不同取样数量下的近似方法程序
N = [10 100 1000 10000];
dx = pi / 2;
for j = 1:4
n = N(j);
fprintf('n = %d\n', n);
% 均匀采样
sum = 0;
for i = 1:n
x = i * dx/n;
sum = sum + dx/n * sin(x);
end
disp(sum);
% 概率密度函数
sum = 0;
for i = 1:n
x = i * dx/n;
px = 8 / (pi^2) * x;
sum = sum + 1 / n * sin(x) / px;
end
disp(sum);
% 随机均匀取点，随机取样本点
sum = 0;
x = random_number(n);
x = [0 sort(x)];
for i = 1:n
sum = sum + sin(x(i+1)) * (x(i+1) - x(i));
end
disp(sum);
end
其中 random_number 函数定义如下
function [x] = random_number(N)
% N 为生成随机数的数目.
y = rand(1, N); % 生成 N 个 0，1 间均匀分布随机数
x = pi * sqrt(y) / 2;
end
