直线和圆弧的生成算法

目录

• 直线生成算法
  • 逐点比较法
  • 数值微分法 (DDA)
  • 中点画线法
  • Bresenham 算法
• 圆弧生成算法
  • 逐点比较法
  • 中点画圆法
  • Bresenham 算法

 

直线生成算法

逐点比较法

所谓逐点比较法，就是在绘图过程中，绘图笔每走一步就与规定图形进行偏差比较，然后决定下一步的走向。

• 偏差判别：判断画笔的当前位置与规定图形的位置之间的偏差，以确定画笔下一步的走步方向
• 画笔走步：画笔在 X 或 Y 方向走一步
• 终点判断：判断画笔的当前位置是否是规定图形的终点
• 偏差计算：计算画笔在当前位置上与规定图形之间的偏差

画直线时，将端点作为原点，按照象限规定走笔的方向，如图所示

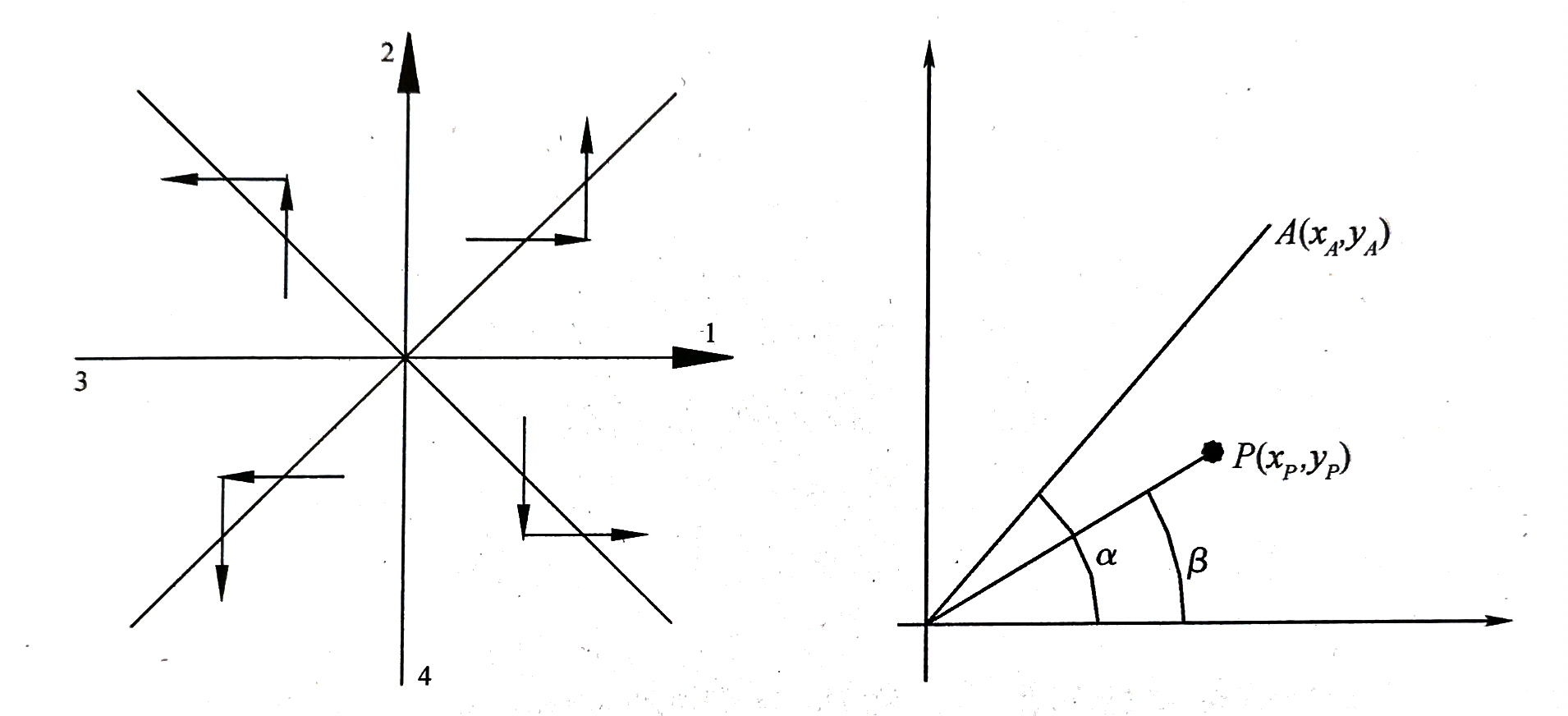
然后，我们将直线的斜率作为偏差计算的原始参数：

\[\Delta = \tan\beta - \tan\alpha = \dfrac{y_P}{x_P} - \dfrac{y_A}{x_A} = \dfrac{y_Px_A-x_Py_A}{x_Px_A} \]

其中 \(A\) 是理想点， \(P\) 是当前画笔位置。实际上，我们只需要考虑 \(\Delta\) 的符号。对于第一象限：

• \(\Delta < 0\) ，笔在直线下方，应该向 \(+Y\) 方向走一步
• \(\Delta\ge 0\) ，笔在直线上方，应该向 \(+X\) 方向走一步

因此，只要计算 \(F = x_Ay_P-x_Py_A\) 即可。

 

考虑第一象限，其它象限的情况是类似的。由于每一步长度为 1 ，可以借此简化偏差计算为递推式。设当前位置为 \(P_1\) ，则若

$$ F_1 = y_1x_A - y_Ax_1 < 0 $$

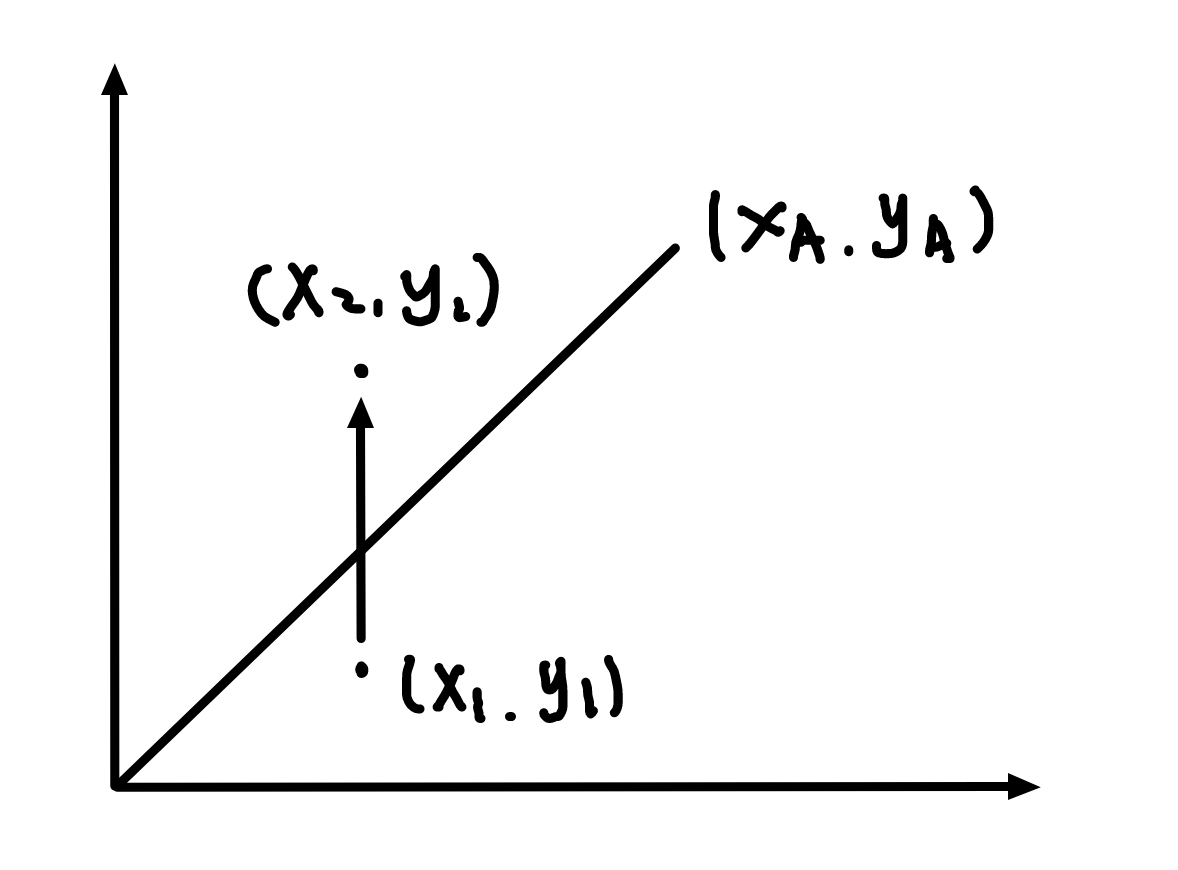
应当向 \(+Y\) 方向走一格，则新的偏差为

\[F_2 = y_2 x_A - y_Ax_2 = y_1x_A-y_Ax_1+x_A = F_1 + x_A \]

而如果 \(F_1\ge 0\) 则向 \(+X\)​ 方向走一格，则新的偏差为

$$ F_2 = y_2 x_A - y_Ax_2 = y_1x_A-y_Ax_1-y_A = F_1 - y_A $$ 因此我们总结得到

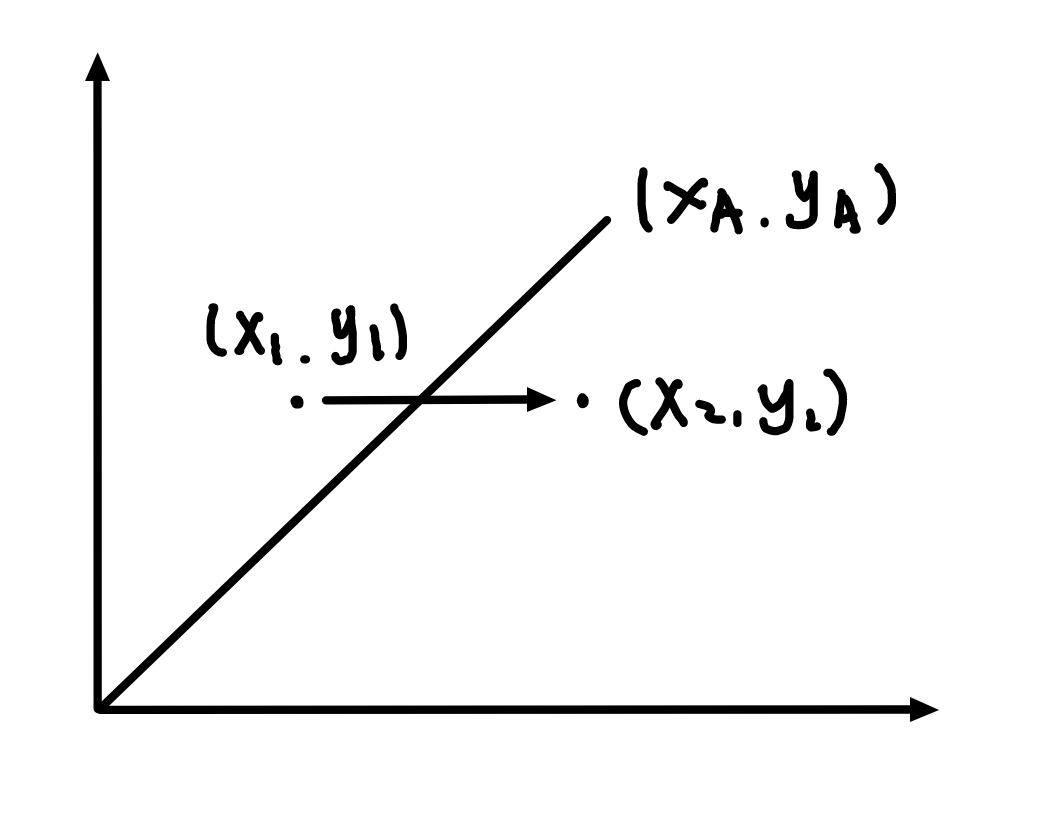
• \(F_i\ge 0\) ，向 \(+X\) 方向走一格，新的偏差为 \(F_{i+1}=F_i-y_A\)
• \(F_i\le 0\) ，向 \(+Y\) 方向走一格，新的偏差为 \(F_{i+1}=F_i+x_A\)

其中 \(F_1=0\) ，因为这里是起点。

 

最后，我们根据笔画的总步数判断是否终止。令 \(N=\Delta X/s +\Delta Y/s\) ，其中 \(s\) 为步长，则总步数为

\[N = (|x_A|+|y_A|) /s \]

每走一步 \(N=N-1\) ，直到为 \(0\) 就停止。

 

数值微分法 (DDA)

数值微分法直接计算要绘制的点的位置。我们假设通过端点 \(P_0(x_0,y_0),P_1(x_1,y_1)\) 绘制线段，则斜率为

\[k = \dfrac{y_1-y_0}{x_1-x_0} \]

我们假设 \(|k|\le 1\) ，此时将 \(x\) 作为主导方向，即 \(x\) 每次递增 \(1\) ，而 \(y\) 递增 \(k\) ，这是因为要保证绘制精度，每个方向的步长不能超过 \(1\) ；从而就有递推式

\[y_{i+1} = kx_{i+1} + b = kx_i+b+k\Delta x = y_i+k\Delta x = y_i + k \]

根据这一原理，我们给出画图算法程序：

void DDALine(HDC hdc, POINT p1, POINT p2, COLORREF color)
{
	double dx = p2.x - p1.x, dy = p2.y - p1.y;
	double k = fabs(dy / dx);

	double x = 0, y = 0;

	// 判断延伸方向
	int sx = (dx > 0) ? 1 : -1;
	int sy = (dy > 0) ? 1 : -1;

	// 如果斜率大于 1 就改变优先级
	bool trans = (k > 1) ? true : false;

	if (trans)
	{
		// y 主导，y++ ，x 增加斜率的倒数
		for (; y <= std::abs(dy); y++, x += 1 / k)
		{
			// 横坐标补充 0.5
			SetPixel(hdc, x * sx + p1.x + 0.5 * sx, int(y * sy + p1.y), color);
		}
	}
	else
	{
		// x 主导，x++ ，y 增加斜率
		for (; x <= std::abs(dx); x++, y += k)
		{
			// 纵坐标补充 0.5
			SetPixel(hdc, x * sx + p1.x, int(y * sy + p1.y + 0.5 * sy), color);
		}
	}
}

需要注意几点：

• 实际使用时需要先将绘图端点移动到原点位置，方便朝不同象限绘制，在绘图时再将端点移回原位
• 由于进行浮点运算后需要转换为整型，因此补充坐标 \(0.5\)

正是因为浮点运算的四舍五入问题，它并不利于硬件实现。

 

中点画线法

首先假设斜率 \(k\in[0,1]\) ，当前像素点为 \((x_P,y_P)\) ，则下一个像素点有两种可能性 \(P_1(x_P+1,y_P),P_2(x_P+1,y_P+1)\) ，如图所示

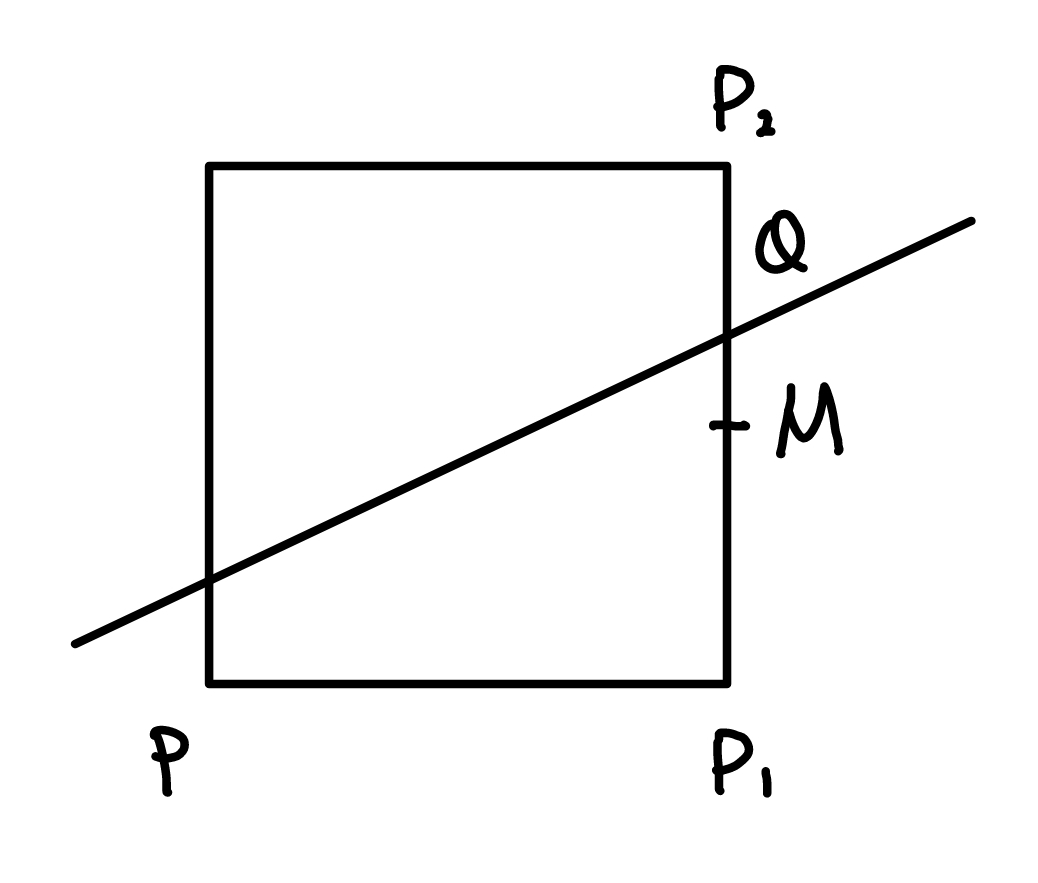
我们根据中点相对直线的位置来判断选择哪个像素点

• 当 \(M\) 在 \(Q\) 下方，则选择 \(P_2\)
• 当 \(M\) 在 \(Q\) 上方，则选择 \(P_1\)

我们知道，过点 \((x_0,y_0),(x_1,y_1)\) 的线段方程为 \(F(x,y)=ax+by+c=0\) ，其中

\[a=y_0-y_1,\quad b=x_1-x_0,\quad c = x_0y_1-x_1y_0 \]

只需要代入点 \(M\) 就可以知道它在 \(F\) 的哪个方位。实际上，构造

\[d = F(M) = F(x_P+1,y_P+0.5) = a(x_P+1)+b(y_P+0.5)+c \]

• 当 \(d<0\) ，则选择 \(P_2\)
• 当 \(d\ge 0\) ，则选择 \(P_1\)

由于每次选择的方向只有两种，我们考虑增量计算来提高效率。假设我们选取 \(P_1\) ，新的中点为 \(M_1(x_P+2,x_P+0.5)\) ，从而

\[d_1 = F(M_1) = F(x_P+2,x_P+0.5) = a(x_P+2)+b(y_P+0.5)+c = d + a \]

选取 \(P_2\) ，新的中点为 \(M_2(x_P+2,x_P+1.5)\) ，从而

\[d_2 = F(M_2) = F(x_P+2,x_P+1.5) = a(x_P+2)+b(y_P+1.5)+c = d + a + b \]

又从 \((x_0,y_0)\) 出发计算 \(d_0\) 为

\[d_0 = F(x_0+1,y_0+0.5) = F(x_0,y_0) + a + 0.5b = a + 0.5b \]

因此我们总结得到

• \(d_i\ge 0\) ，选取 \(P_1\) ， \(d_{i+1} = d_i+a\)
• \(d_i< 0\) ，选取 \(P_2\) ， \(d_{i+1} = d_i+a+b\)

其中 \(d_0=a+0.5b\) ，因为这里是起点。

 

注意到上面的所有运算中只出现了浮点数 \(0.5\) ，而我们的判断只与 \(d\) 的符号相关，因此用 \(2d\) 来代替 \(d\) ，得到只有整数运算的程序：

void Midpointline(HDC hdc, POINT p1, POINT p2, COLORREF color)
{
	int a = -std::abs(p1.y - p2.y), b = std::abs(p2.x - p1.x);
	// 中点距离，向右/下移动的距离的增量 dd1 ，向右下移动的距离的增量 dd2
	int d, dd1, dd2;

	bool trans = (a + b) > 0 ? false : true;	// 判断是否需要交换 x y 优先级
	d = trans ? (a + 2 * b) : (2 * a + b);		// d ：下一个像素中点距离 * 2 两种情况 F(x+0.5,y+1) 或 F(x+1,y+0.5)
	dd1 = trans ? (2 * b) : (2 * a);		    // 下一像素距离增量 * 2 ： d1  正右方 F(x+1,y) 正下方 F(x,y+1)
	dd2 = 2 * (a + b);						   // d2 “右上方” F(x+1,y+1) ，注意 y 方向向下

	// 判断延伸方向
	int sy = (p1.y - p2.y) > 0 ? -1 : 1;
	int sx = (p2.x - p1.x) > 0 ? 1 : -1;

	int x = 0, y = 0;	// 初始位置
	bool t = true;		// 循环条件

	// 绘制当前点
	SetPixel(hdc, x + p1.x, y + p1.y, color);

	while (t)
	{
		// 以 y 方向为主导，y++ ，否则 x++ 
		trans ? y++ : x++;
		// 根据主导方向和中点距离符号判断另一个方向的增加
		if (trans)
		{
			// 当 d < 0 ，应当向 正下方 F(x,y+1) 移动，否则向 F(x+1,y+1) 移动 x++						
			d < 0 ? d += dd1 : (x++, d += dd2);
		}
		else
		{
			// 当 d < 0 ，应当向 F(x+1,y+1) 移动 y++，否则向 正右方 F(x+1,y) 移动
			d < 0 ? (y++, d += dd2) : d += dd1;
		}
		t = trans ? (y < -a) : (x < b);						  // 结束条件值
		SetPixel(hdc, x * sx + p1.x, y * sy + p1.y, color);		// 绘制当前点
	}
}

 

Bresenham 算法

Bresenham 算法是计算机图形学领域使用最广泛的直线扫描转换算法。这里仍然假定斜率 \(k\in[0,1]\) ，类似于中点法，由一个误差项符号决定下一个像素点。

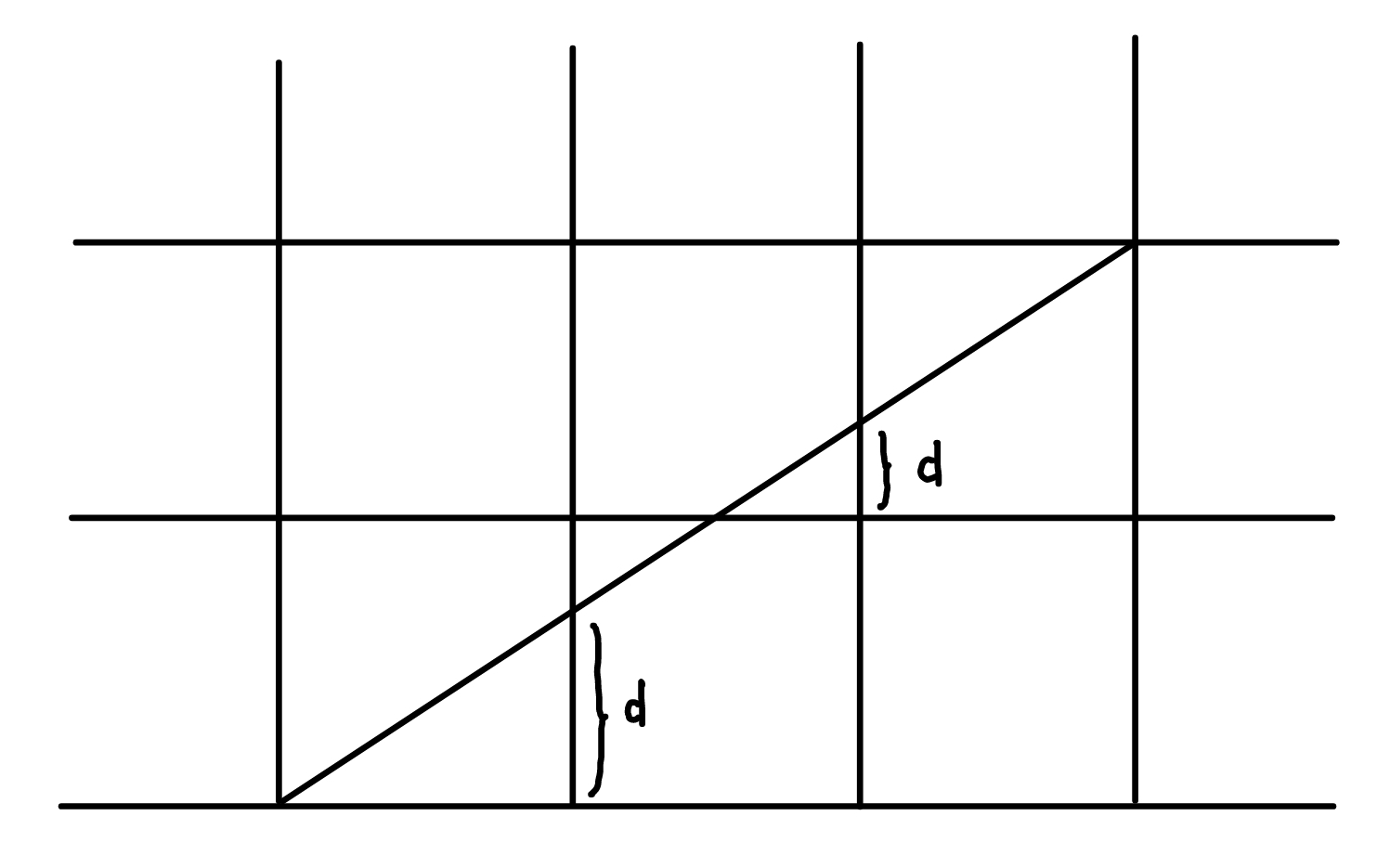
假设当前像素点为 \((x_i,y_i)\) ，则下一个像素点可能为 \((x_i+1,y_i),(x_i+1,y_i+1)\) ，我们保存一个误差项 \(d\) ，用于记录直线与网格线交点与 \((x_i+1,y_i)\) 的距离。每当 \(x\) 增加 \(1\) ，就将 \(d\) 增加 \(k\) ，当 \(d\ge1\) 就把它减去 \(1\) ，这样就保证 \(d\in[0,1]\) ；然后，当 \(d\ge 0.5\) ，就选择 \((x_i+1,y_i+1)\) ，否则选择 \((x_i+1,y_i)\) 。

为了方便计算，我们令 \(e=d-0.5\) ，这样就可以只通过 \(e\) 的符号来判断选择点

• \(e\ge 0\) ，选择 \((x_i+1,y_i+1)\)
• \(e<0\) ，选择 \((x_i+1,y_i)\)

然后，每次增加 \(k\) 以及减去 \(0.5\) 会导致浮点运算，因此乘上 \(2\cdot dx\) 得到 \(2\cdot e\cdot dx\) 来进行判断，每次 \(e=e+2\cdot dy\) ，就得到只有整型运算的算法程序：

void Bresenhamline(HDC hdc, POINT p1, POINT p2, COLORREF color)
{
	int x = 0, y = 0;
	int dx = std::abs(p2.x - p1.x);
	int dy = std::abs(p2.y - p1.y);

	bool trans = (dy > dx) ? true : false; // 判断是否转换 xy 主导地位
	int d = trans ? dy : dx;			   // 绘图范围
	int e = trans ? -dy : -dx;			   // 判断误差

	// 延伸方向
	int sy = (p2.y - p1.y) > 0 ? 1 : -1;
	int sx = (p2.x - p1.x) > 0 ? 1 : -1;

	for (int i = 0; i <= d; i++)
	{
		// 绘制当前点
		SetPixel(hdc, x * sx + p1.x, y * sy + p1.y, color);
		if (trans)
		{
			y++;
			e += 2 * dx;
			if (e >= 0)
			{
				x++;
				e -= 2 * dy;
			}
		}
		else
		{
			x++;
			e += 2 * dy;
			if (e >= 0)
			{
				y++;
				e -= 2 * dx;
			}
		}
	}
}

 

测试绘图程序：

case WM_PAINT:
{
	PAINTSTRUCT ps;
	HDC hdc = BeginPaint(hWnd, &ps);
	// TODO: 在此处添加使用 hdc 的任何绘图代码...
	int r = 100;
	int N = 20;

	POINT c1 = {150, 200};

	for (int i = 0; i < N; i++)
	{
		POINT p = {c1.x + int(r * cos(2 * PI / N * i)), c1.y + int(r * sin(2 * PI / N * i))};
		Bersenhamline(hdc, c1, p, RGB(255, 0, 0));
	}

	EndPaint(hWnd, &ps);
}

 

圆弧生成算法

逐点比较法

由于圆弧不但有四个象限的区分，还有顺时针画和逆时针画的区别，因此逐点比较法需要考虑 8 种不同情况

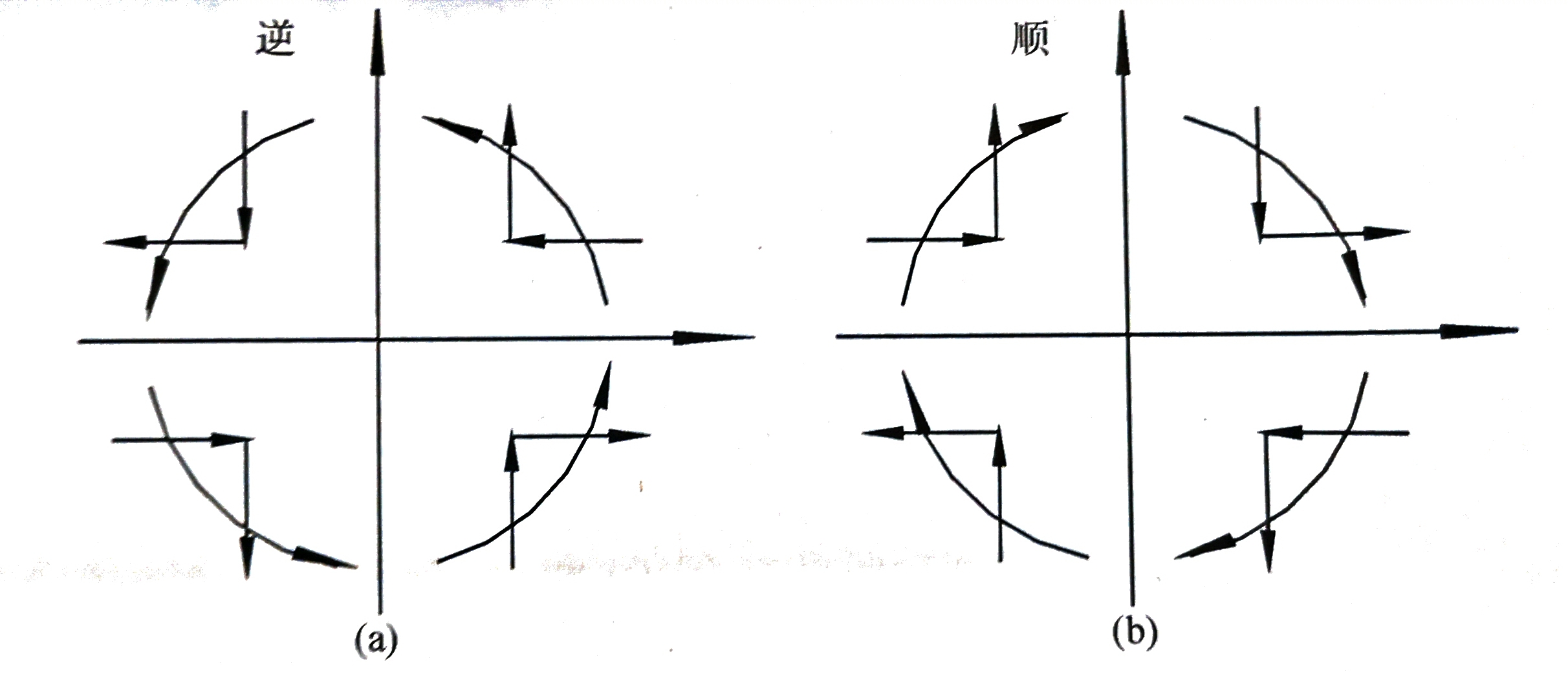
我们只考虑在第二象限的顺时针画圆算法，其它情况是完全类似的。

逐点比较法保存一个误差项

\[\Delta = R_P-R = \sqrt{x_P^2+y_P^2} - R \]

为了方便起见，用平方来代替

\[F = R_P^2-R^2 = (x_P^2+y_P^2) - R^2 \]

类似于前，作如下判断

• \(F\ge0\) ，说明 \(P\) 在圆弧外，应该向 \(+X\) 方向（朝内）移动
• \(F<0\) ，说明 \(P\) 在圆弧内，应该向 \(+Y\) 方向（朝外）移动

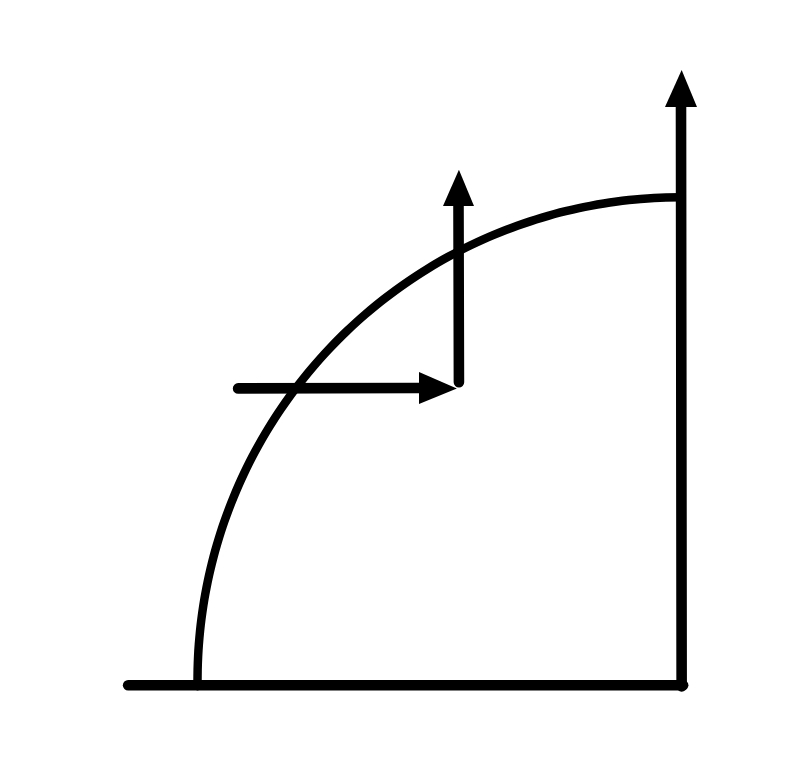
我们从左下角的点 \((-R,0)\) 出发，首先会向 \(+X\) 方向移动。然后用递推式简化计算：当向 \(+X\) 方向移动

\[F_1 = (x+1)^2 + y^2 - R^2 = F +2x+1 \]

当向 \(+Y\) 方向移动

\[F_1 = x^2 + (y+1)^2 - R^2 = F +2y+1 \]

于是我们得到如下算法程序：

// 顺向画圆弧
void pointwiseCircle(HDC hdc, POINT c, int r, COLORREF color)
{
	int x = -r, y = 0;
	int F = 0;

	while (x <= 0)
	{
		SetPixel(hdc, x + c.x, y + c.y, color);
		if (F >= 0)
		{
			F += 2 * x + 1;
			x++;
		}
		else
		{
			F += 2 * y + 1;
			y++;
		}
	}
}

// 逆向画圆弧
void pointwiseAntiCircle(HDC hdc, POINT c, int r, COLORREF color)
{
	int x = 0, y = r;
	int F = 0;

	while (y >= 0)
	{
		SetPixel(hdc, x + c.x, y + c.y, color);
		if (F >= 0)
		{
			F += -2 * y + 1;
			y--;
		}
		else
		{
			F += -2 * x + 1;
			x--;
		}
	}
}

 

测试绘图程序：

// 逐点画圆法，第二象限顺圆，逆圆
pointwiseCircle(hdc, { 200,400 }, r, RGB(255, 0, 0));
pointwiseAntiCircle(hdc, { 300,400 }, r, RGB(255, 0, 0));

 

中点画圆法

如果构造函数 \(F(x,y)=x^2+y^2-R^2\) ，那么就可以用之前的中点法来作为判断标准。

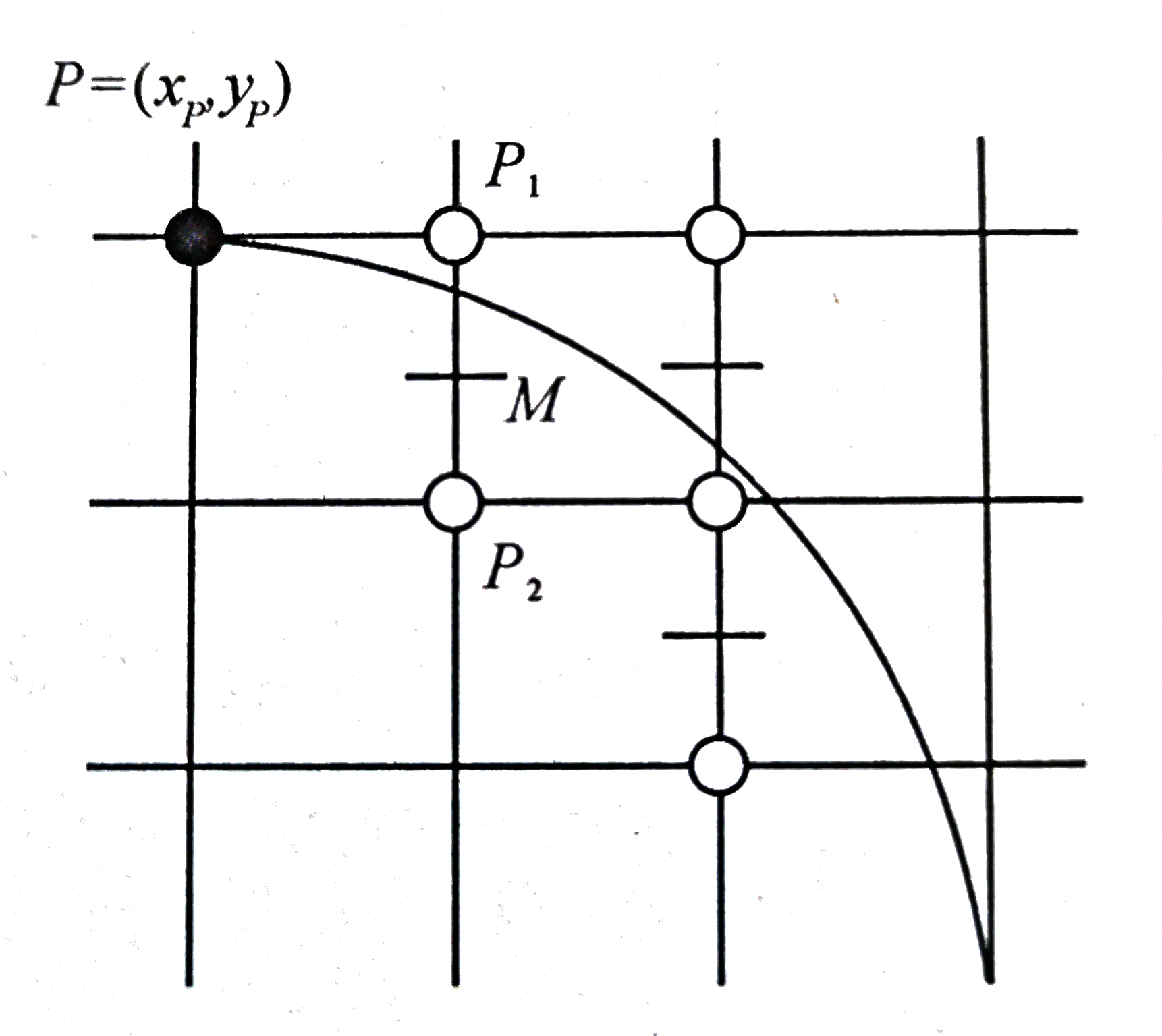
对每一当前像素点 \(P\) ，判断选择 \(P_1\) 或 \(P_2\) ，只需要计算判别式

\[d = F(M) = F(x+1,y-0.5) = (x+1)^2 + (y-0.5)^2 - R^2 \]

如果 \(d\ge0\) ，则 \(M\) 在外部，选择向内的点 \(P_2\) ，此时中点 \(M_1\) 在 \(P_2\) 右下方

\[d_1 = F(M_1) = F(x+2,y-1.5) = d +2(x-y) + 5 \]

相反的，如果 \(d<0\) ，则选择 \(P_1\) ，此时中点 \(M_1\) 在 \(P_1\) 右下方

\[d_1 = F(M_1) = F(x+2,y-0.5) = d +2x + 3 \]

这样就得到了递推关系，假设初始绘制点为 \((0,R)\) ，则有

\[d = F(1,R-0.5) = 1.25 - R \]

可以乘 \(8\) 来避免浮点数运算。

Bresenham 算法

考虑圆心在原点，半径为 \(R\) ，取 \((0,R)\) 为起点，画第一象限顺圆弧。如果当前像素点为 \((x,y)\) ，则考虑候选像素 \(H,D,V\) ，如图所示

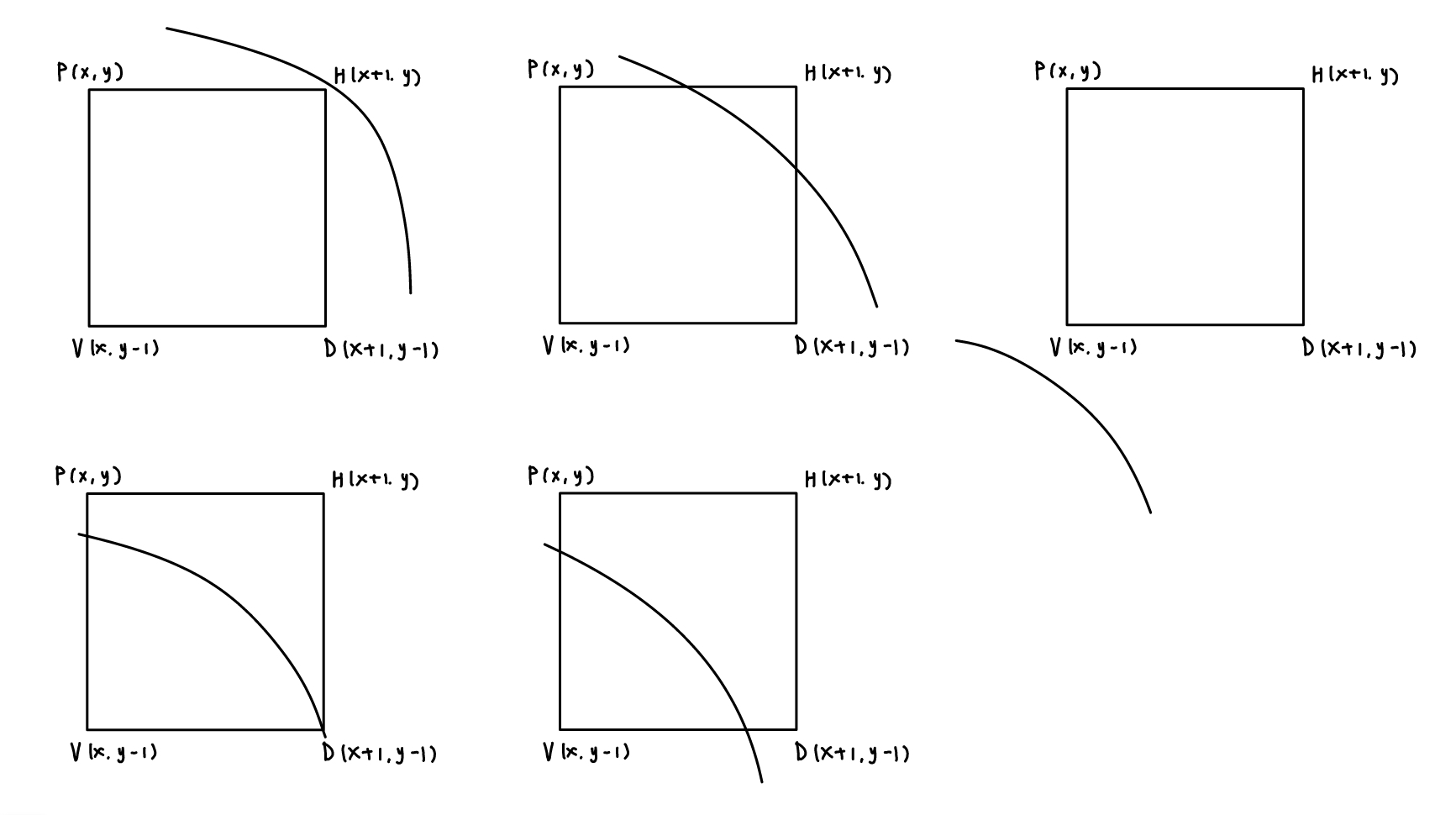
共有 5 种可能的关系

• \(H,D,V\) 都在圆内
• \(H\) 在圆外， \(D,V\) 在圆内
• \(D\) 在圆上， \(H\) 在圆外， \(V\) 在圆内
• \(H,D\) 在圆外， \(V\) 在圆内
• \(H,D,V\) 都在圆外

我们保存三个距离差值

\[\begin{aligned} D_h &= (x+1)^2+y^2-R^2\\ D_d &= (x+1)^2+(y-1)^2-R^2\\ D_v &= x^2+(y-1)^2-R^2 \end{aligned} \]

它们的符号分别表明了是否在圆内的信息。

 

选择 \(D_d\) 作为判断的开始：

• 如果 \(D_d=0\) ，那么 \(D\) 在圆上，直接选择 \(D\) 即可；

• 如果 \(D_d>0\) ，那么 \(D\) 在圆外，应该向内靠近

  • 计算 \(d_{DV} = D_d+D_v\) 的符号，如果为正，则取 \(V\) ；否则取 \(D\)

• 如果 \(D_d<0\) ，那么 \(D\) 在圆内，应该向外移动

  • 计算 \(d_{DH} = D_d+D_h\) 的符号，如果为正，则取 \(D\) ；否则取 \(H\)

 

最后，为了简便计算，推导递推式：

若取 \(H(x+1,y)\) ，则新的 \(D_1(x+2,y-1)\) 满足

\[D_{d_1} = ((x+1)+1)^2 + (y-1)^2 - R^2 = D_d + 2(x+1)+1 \]

若取 \(D(x+1,y-1)\) ，则新的 \(D_1(x+2,y-2)\) 满足

\[D_{d_1} = ((x+1)+1)^2 + ((y-1)-1)^2 - R^2 = D_d + 2(x+1)-2(y-1)+2 \]

若取 \(V(x,y-1)\) ，则新的 \(D_1(x+1,y-2)\) 满足

\[D_{d_1} = (x+1)^2 + ((y-1)-1)^2 - R^2 = D_d - 2(y-1) + 1 \]

注意到新选择的点的坐标恰好对应增量，例如

• \(H(x+1,y)\) 对应增量 \(2(x+1)+1\) ，因此可以先取 x++ ，然后直接计算增量 \(2x+1\) ；
• 类似地，对于 \(D(x+1,y-1)\) ，先取 x++,y-- ，然后计算增量 \(2(x-y+1)\) ；
• 对于 \(V(x,y-1)\) ，先取 y-- ，然后计算增量 \(-2(y-1)+1\)

 

接着是 \(d_{DV},d_{DH}\) 的计算，根据定义就有

\[d_{DH} = D_h + D_d = 2D_d+2y-1\\ d_{DV} = D_v + D_d = 2(D_d-x)-1 \]

结合点的坐标旋转，就得到任意象限中的任意弧度圆弧的生成算法程序：

// 逆时针旋转 90 度的 n 倍
POINT rotate(int x, int y, int n)
{
	POINT p = { x,y };
	// 根据 n 判断要旋转几个 90 度
	n = n % 4;
	switch (n)
	{
	case 0: break;
	case 1:
	{
		int tmp = p.x;
		p.x = -p.y;
		p.y = tmp;
	}
	case 2:
	{
		p.x = -p.x;
		p.y = -p.y;
	}
	case 3:
	{
		int tmp = p.y;
		p.y = -p.x;
		p.x = tmp;
	}
	}
	return p;
}

void BresenhamCircle(HDC hdc, POINT c, int r, double _arg1, double _arg2, COLORREF color)
{
	// 下一个选择的点
	enum class NextPoint
	{
		H, D, V
	};

	// 下一个选择的点
	NextPoint nextPoint;

	// 调整角度参数，全部改为顺时针画圆
	double arg1 = (_arg1 > _arg2) ? _arg1 : _arg2;
	double arg2 = (_arg1 > _arg2) ? _arg2 : _arg1;

	// 记录旋转的次数，转到第一象限
	int n = arg2 * 2 / PI;

	// 以 (0,0) 为原点，转换为第一象限，确定 xy 位置
	int x = r * cos(arg1 - n * PI / 2), y = r * sin(arg1 - n * PI / 2);

	// 距离判断条件
	int Dd = 2 * (1 - r);
	int dHD, dDV;

	// 结束条件
	int end = r * sin(arg2 - n * PI / 2);

	while (y >= end)
	{
		POINT p = rotate(x, y, n);						// 旋转点到正确的象限
		SetPixel(hdc, p.x + c.x, p.y + c.y, color);		// 绘制当前点

		// 根据 D 在圆内外分情况讨论
		if (Dd < 0)
		{
			// 选择 H 或 D，dHD = Dh + Dd
			dHD = 2 * (Dd + y) - 1;
			nextPoint = (dHD <= 0) ? NextPoint::H : NextPoint::D;
		}
		else if (Dd > 0)
		{
			// 选择 V 或 D，dDV = Dd + Dv
			dDV = 2 * (Dd - x) - 1;
			nextPoint = (dDV <= 0) ? NextPoint::D : NextPoint::V;
		}
		else
		{
			// D 在圆上，选择 D
			nextPoint = NextPoint::D;
		}
		switch (nextPoint)
		{
		case NextPoint::H:
			// H = (x+1,y)
			x++;
			Dd += 2 * x + 1;
			break;
		case NextPoint::D:
			// D = (x+1,y-1)
			x++, y--;
			Dd += 2 * (x - y + 1);
			break;
		case NextPoint::V:
			// V = (x,y-1)
			y--;
			Dd += (-2 * y + 1);
			break;
		}
	}
}

 

测试绘图程序：

case WM_PAINT:
{
	PAINTSTRUCT ps;
	HDC hdc = BeginPaint(hWnd, &ps);
	// TODO: 在此处添加使用 hdc 的任何绘图代码...
	POINT c = { 200,200 };
	int r = 100;
	BresenhamCircle(hdc, c, r, PI / 2, PI / 6, RGB(255, 0, 0));
	BresenhamCircle(hdc, c, r, PI, PI * 2 / 3, RGB(255, 0, 0));
	BresenhamCircle(hdc, c, r, PI * 3 / 2, PI * 7 / 6, RGB(255, 0, 0));
	BresenhamCircle(hdc, c, r, 2 * PI, PI * 5 / 3, RGB(255, 0, 0));

	EndPaint(hWnd, &ps);
}