定义 设 \(\xi(\omega)\) 是定义在概率空间 \(\{\Omega, F,P\}\) 上的单值实函数,且对于 \(\mathbb{R}\) 上的任一波雷尔集 \(B\) 有
\[\xi^{-1}(B) = \{\omega:\xi(\omega)\in B \}\in F
\]
则称 \(\xi(\omega)\) 为随机变量,而称 \(\{P(\xi(\omega)\in B) \}\) 为随机变量的概率分布.
定义 若随机变量 \(\xi_1(\omega),\xi_2(\omega),\cdots,\xi_n(\omega)\) 定义在同一概率空间 \((\Omega,F,P)\) 上,就称
\[\xi(\omega) = (\xi_1(\omega),\xi_2(\omega),\cdots,\xi_n(\omega))
\]
为 \(n\) 维随机变量.
离散型分布
定义 离散型随机变量的分布列如下
\[\left[
\begin{matrix}
x_1 & x_2 & \cdots & x_n\\
p(x_1) & p(x_2) & \cdots & p(x_n)
\end{matrix}
\right]
\]
随机变量在离散点处取得对应的概率.
定义 离散型二维联合分布列
\[P(\xi=x_i,\eta=y_j) = p_{ij},\quad i,j=1,2,\cdots
\]
记作 \(p(x_i,y_j),\quad i,j=1,2,\cdots\) .
定义 边际分布是固定其中一个分量,取另一个分量的分布的和
\[P(\xi=x_i) = \sum_{j=1}^{+\infty}P(\xi=x_i,\eta=y_j) = \sum_{j=1}^{+\infty}p_{ij} = p_i\\
P(\eta=y_j) = \sum_{i=1}^{+\infty}P(\xi=x_i,\eta=y_j) = \sum_{i=1}^{+\infty}p_{ij} = p_j
\]
定义 离散随机向量分布函数是在一个矩形区域中的概率
\[F(x_1,\cdots,x_n) = P(\xi_1\le x_1,\cdots,\xi_n\le x_n)
\]
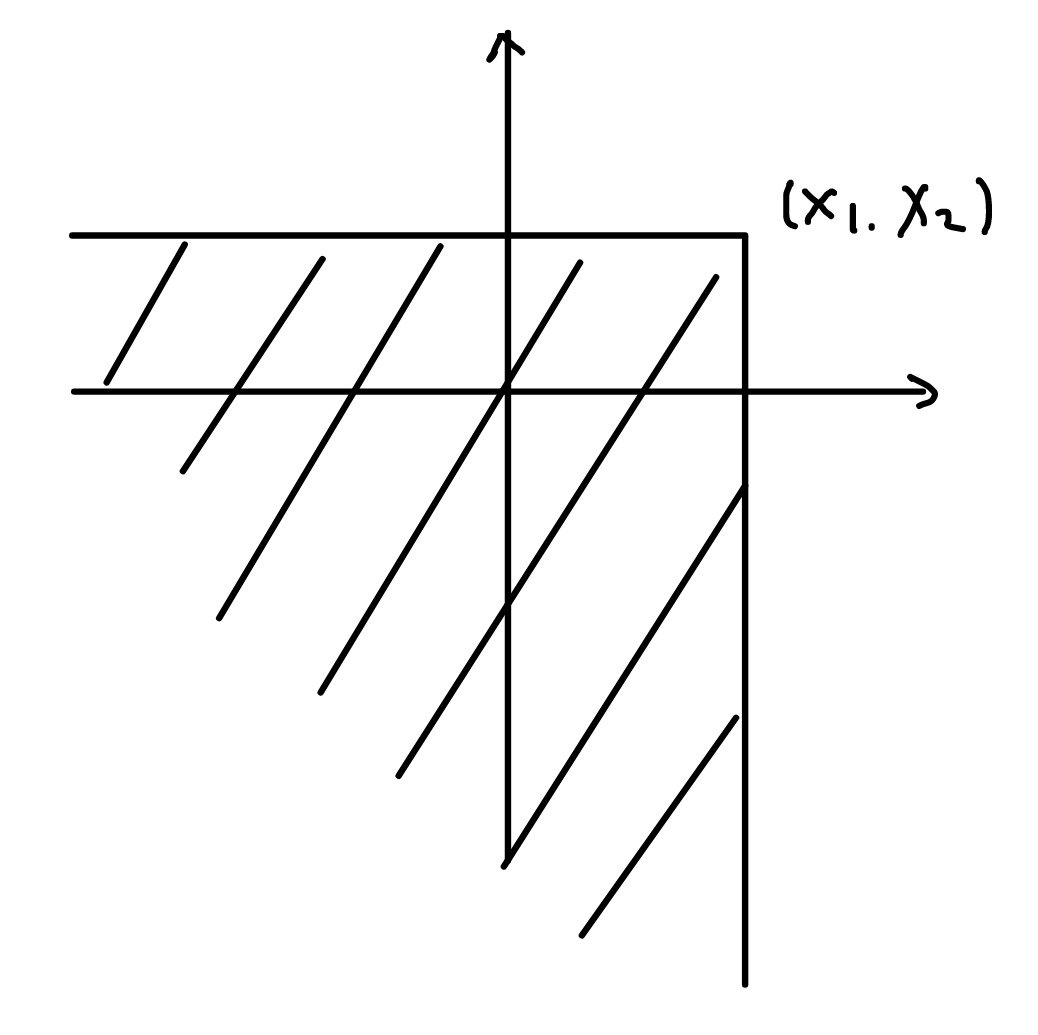
它是左下角的区域中的概率总和.
连续型分布
定义 分布函数具有形式
\[F(x) = P(\xi\le x),\quad -\infty<x<+\infty
\]
它是随机变量 \(\xi(\omega)\) 的分布函数.
定义 连续随机变量 \(\xi\) 应当可以取得一个区间中的一切值,并且存在某个非负的可积函数 \(p(x)\) ,使得分布函数满足
\[F(x) = \int_{-\infty}^x p(y)dy,\quad -\infty<x<+\infty
\]
则称 \(p(x)\) 为 \(\xi\) 的密度函数.
定义 联合密度函数为 \(p(x_1,\cdots,x_n)\) ,则分布函数为
\[F(x_1,\cdots,x_n) = \int_{-\infty}^{x_1}\cdots\int_{-\infty}^{x_n}p(y_1,\cdots,y_n)dy_1\cdots dy_n
\]
它也表示一个矩形区域中的概率总和.
定义 二维边际分布定义为
\[F_{\xi}(x) = F(x,\infty) = \int_{-\infty}^{x}\int_{-\infty}^{+\infty}p(u,v)dudv = \int_{-\infty}^{x}p_{\xi}(u)du
\]
其中被积函数称为边际密度
\[p_{\xi}(u) = \int_{-\infty}^{+\infty}p(u,v)dv,\quad p_{\eta}(u) = \int_{-\infty}^{+\infty}p(u,v)du
\]
对密度函数的其中一个变量作积分得到边际密度.
随机变量独立性
定义 离散型随机向量
\[P(\xi=x_i,\eta=y_j) = P(\xi=x_i)P(\eta=y_j),\quad i,j=1,2,\cdots
\]
则称 \(\xi,\ \eta\) 相互独立;可以发现
\[F(x,y) = P(\xi\le x,\eta\le y) = P(\xi\le x)P(\eta\le y) = F_{\xi}(x)F_{\eta}(y)
\]
也就是说,概率的相互独立意味着分布相互独立,只需
\[P(\xi=i,\eta=j) = P(\xi=i)P(\eta=j)
\]
即可证明离散联合分布列 \((\xi,\eta)\) 中 \(\xi,\eta\) 独立.
定义 连续型随机向量
\[F(x,y) = F_{\xi}(x)F_{\eta}(y)
\]
则称 \(\xi,\ \eta\) 相互独立;类似的有 \(p(x,y) = p_{\xi}(x)p_{\eta}(y)\) 当且仅当 \(\xi,\eta\) 相互独立.
离散型条件分布
定义 若 \(P(\xi=x_i)>0\) ,则
\[P(\eta=y_j|\xi=x_i) = \dfrac{P(\xi=x_i,\eta=y_j)}{P(\xi=x_i)} = \dfrac{p_{ij}}{p_i},\quad i,j=1,2,\cdots
\]
称为在 \(\xi=x_i\) 下 \(\eta\) 的条件分布,记为 \(P_{\eta|\xi}(y_j|x_i)\) .
定义 条件分布函数为
\[P(\eta\le y|\xi=x_i) = \sum_{y_j\le y}P(\eta=y_j|\xi=x_i)
\]
容易证明 \(P(\eta=y_j|\xi=x_i) = P(\eta=y_j)\) 当且仅当 \(\xi,\eta\) 相互独立.
连续型条件分布
定义 若在 \(x\) 处边际密度
\[p_{\xi}(x) = \int_{-\infty}^{+\infty}p(u,v)dv > 0
\]
则称
\[P(\eta\le y|\xi=x) = \int_{-\infty}^y\dfrac{p(x,v)}{p_{\xi}(x)}dv
\]
为在 \(\xi=x\) 下 \(\eta\) 的条件分布,记为 \(P_{\eta|\xi}(y|x)\) .
于是我们得到连续分布下的贝叶斯公式
\[P_{\eta|\xi}(y|x) = \dfrac{P_{\xi|\eta}(x|y)p_{\eta}(y)}{\int_{-\infty}^{+\infty}P_{\xi|\eta}(x|v)p_{\eta}(v)dv}
\]
上面是 \(x,y\) 同时发生的概率,下面是 \(x\) 发生的概率.
注意到当 \(x\) 发生时 \(A\) 发生的概率可以看作是一个关于 \(x\) 的函数,我们考虑
\[g(x) = P(A|X=x)
\]
从而有全概率公式
\[P(A) = \int_{-\infty}^{+\infty}g(x)p_X(x)dx
\]
它表示的是 \(A\) 发生的概率是每一个 \(x\) 发生时 \(A\) 发生的概率的总和.
卷积公式
离散分布 \(\zeta = \xi + \eta\) 的分布列为
\[P(\zeta=r) = \sum_{k=0}^rP(\xi=k)P(\eta=r-k)
\]
根据定义很容易验证.
连续型分布 \(\eta = f(\xi)\) 的分布函数为
\[G(y) = P(\eta \le y) = P(f(\xi)\le y) = \int_{x\in D}p(x)dx,\quad D=\{x|f(x)\le y\}
\]
限制 \(f(x)\) 严格单调, \(f^{-1}(y)\) 有连续导数,则 \(\eta = f(\xi)\) 是连续型随机变量,有密度函数
\[g(y) = \left\{
\begin{aligned}
&p(f^{-1}(y))\left|\left[f^{-1}(y)\right]^{\prime}\right|,\quad &y\in f(x)\\
&0,\quad &\mathrm{otherwise}
\end{aligned}
\right.
\]
\(Proof.\) 只需利用定义
\[\int_{-\infty}^{y}g(v)dv = G(y) = P(f(\xi)\le y) = P(\xi\le f^{-1}(y)) = \int_{-\infty}^{f^{-1}(y)}p(x)dx = \int_{-\infty}^{x}p(f^{-1}(y))\left|\left[f^{-1}(y)\right]^{\prime}\right|dy
\]
当 \(y\notin f(x)\) ,显然有密度为 \(0\) .
令 \(\eta = f(\xi_1,\cdots,\xi_n)\) ,则有分布函数
\[F_{\eta}(y) = P(f(\xi_1,\cdots,\xi_n)\le y) = \int_{f(x_1,\cdots,x_n)\le y}p(x_1,\cdots,x_n)dx_1\cdots dx_n
\]
这是计算所有此类分布函数的通用方式.
通过上述公式,使用类似的方法,我们计算出以下几种常见情况:
- 若 \(\eta = \xi_1+\xi_2\) ,则有密度函数
\[p_{\eta}(z) = \int_{-\infty}^{+\infty}p(x,z-x)dx
\]
当 \(\xi_1,\xi_2\) 相互独立,则有
\[p_{\eta}(z) = \int_{-\infty}^{+\infty}p_{\xi_1}(x)p_{\xi_2}(z-x)dx
\]
对于 \(\eta = \xi_1-\xi_2\) ,只需将其中的符号反转
\[p_{\eta}(z) = \int_{-\infty}^{+\infty}p(x,x-z)dx
\]
- 若 \(\eta = \frac{\xi_1}{\xi_2}\) ,则有密度函数
\[p_{\eta}(z) = \int_{-\infty}^{+\infty}p(zx,x)|x|dx
\]
如果计算 \(\eta = \xi_1\xi_2\) ,先计算 \(1/\xi_2\) ,这只需要取密度函数的倒数,然后应用上式.
次序统计量
设 \(\xi_1,\cdots,\xi_n\) 独立同分布,分布函数为 \(F(x)\) ,定义
\[\xi_1^{*} = \min\{\xi_1,\cdots,\xi_n\},\quad \xi_n^{*} = \max\{\xi_1,\cdots,\xi_n\}
\]
这里 \(\min\) 是对每一个给定的事件 \(A\) ,取 \(\xi_i^*(A) = \min\{\xi_1(A),\cdots,\xi_n(A) \}\) ,而 \(\max\) 也是类似的;则我们有 \(\xi_n^*\) 的分布函数为
\[\begin{aligned}
P(\xi_n^*\le x) &= P(\xi_1\le x,\cdots,\xi_n\le x)\\
&= P(\xi_1\le x)\cdots P(\xi_n\le x)\\
&= [F(x)]^n
\end{aligned}
\]
\(\xi_1^*\) 的分布函数为
\[\begin{aligned}
P(\xi_1^*\le x) &= 1-P(\xi_1^*> x)\\
&= 1- P(\xi_1> x,\cdots,\xi_n> x)\\
&= 1- P(\xi_1> x)\cdots P(\xi_n> x)\\
&= 1-[1-F(x)]^n
\end{aligned}
\]
\((\xi_1^*,\xi_n^*)\) 的联合分布为
\[\begin{aligned}
F(x,y) &= P(\xi_1^*\le x,\xi_n^*\le y)\\
&= P(\xi_n^*\le y) - P(\xi_1^*> x,\xi_n^*\le y)\\
&= [F(y)]^n - P\left(\cap_{i=1}^n(x<\xi_i\le y)\right)
\end{aligned}
\]
- 当 \(x<y\) , \(F(x,y) = [F(x)]^n - [F(y)-F(x)]^n\) ;
- 当 \(x\le y\) , \(F(x,y) = [F(y)]^n\) .
随机向量变换
对 \(f_j(x_1,\cdots,x_n),\ j=1,\cdots,n\) ,若有唯一反函数组 \(x_i=x_i(y_1,\cdots,y_n),\ i=1,\cdots,n\) ,且
\[J = \dfrac{\partial(x_1,\cdots,x_n)}{\partial(y_1,\cdots,y_n)} \neq 0
\]
则 \((\eta_1,\cdots,\eta_n) = (f_1,\cdots,f_n)\) 为随机向量,当 \((y_1,\cdots,y_n)\in(f_1,\cdots,f_n)\) ,有密度函数
\[q(y_1,\cdots,y_n) = p(x_1(y_1,\cdots,y_n),\cdots,x_n(y_1,\cdots,y_n))|J|
\]
这也就是将随机向量 \((\xi_1,\cdots,\xi_n)\) 变换为 \((\eta_1,\cdots,\eta_n)\) 后的密度函数.
如果有 \(k\) 个反函数组 \(x_i^j=x_i^j(y_1,\cdots,y_n),\ i=1,\cdots,n,\ j=1,\cdots,k\) ,即可能存在多个反函数,且有
\[J^j = \dfrac{\partial(x_1^j,\cdots,x_n^j)}{\partial(y_1,\cdots,y_n)} \neq 0
\]
那么密度函数是它们的直接相加
\[q(y_1,\cdots,y_n) = \sum_{j=1}^{k}p(x_1^j(y_1,\cdots,y_n),\cdots,x_n^j(y_1,\cdots,y_n))|J^j|
\]
需要注意反函数的定义域,在定义域外, \(q(y_1,\cdots,y_n) = 0\) .



