Octave 使用方法

目录

• 查询和退出
• 数据类型
• 变量
• 向量及矩阵
  • 特殊向量
  • 向量函数
  • 访问元素
  • 向量运算
  • 创建矩阵
  • 矩阵运算
• 字符串
• 运算符
  • 关系运算
  • 逻辑运算
• 数值计算
  • 计时方法
  • 函数求导
  • 数值求导
  • 求解线性方程组
  • 多项式
  • 插值函数
• 脚本
  • 全局变量
  • 数学函数
  • 输入输出
  • 载入和保存
  • 条件语句
  • 循环语句
  • 函数
• 绘图方法
  • 图形窗口
  • 基本绘图函数
  • 直方图
• package

 

查询和退出

使用 disp 命令输出字符串， help 命令查看帮助

help func;				% 帮助

 

输入 quit 退出 octave

quit					% 退出

 

数据类型

变量	含义
ans	Matlab 中的默认变量
pi	圆周率
eps	计算机中的最小数，浮点运算的相对精度
inf	无穷大，如 1/0
NaN	不定值，如 0/0 0*∞
i / j	复数中的虚数单位
realmin	最小可用正实数
realmax	最大可用正实数

 

数字格式化命令

格式	含义
format short	5 位定点表示
format long	15 位定点表示
format short e	5 位浮点表示
format long e	15 位浮点表示
format short g	5 位定点和 5 位浮点中自动选择最好格式表示
format long g	15 位定点和 15 位浮点中自动选择最好格式表示
format hex	16 进制格式表示
format +	在矩阵中，用符号 + - 和空格表示正号、负号和零

使用时直接输入命令即可

 

基本运算符

运算	作用
+ - * / ^ \	普通加减乘除、幂运算和左除
.* ./ .^ .\	点乘，点除，点乘幂和点左除

 

变量

Octave 变量区分大小写，解释性语言不需要指定变量类型。变量有几种操作命令：

clear 		 	    % 清除所有变量
clear variable 		% 清除指定变量

其中 % 开头的文字是注释，命令末尾的分号不是必须的，如果不在语句结尾加上分号，会输出语句的结果；加上分号则会隐藏结果

 

通过如下函数获取变量的信息

size(var);		% 变量的尺寸
length(var);	% 变量的长度

设置小数位数

vpa(x, n); 		% 显示 x 的 n 位小数

 

向量及矩阵

用方括号括起来的元素表示矩阵和向量，在方括号中由空格或者逗号隔开的一组数据被定义为行向量，而由分号或者回车隔开的一组数据被定义为列向量；实际使用时

% 给出向量
re = [

1 2

3 4

...

];

% 定义矩阵
X = [2 3 4;5 6 7;8 9 10]

使用 ... 进行换行连接，例如

Y = [1 2 3 ...
4 5 6]

它等价于

Y = [1 2 3 4 5 6]

 

可以用向量初始化向量，例如

a = [2 3 4]
b = [a 5]

 

特殊向量

冒号可以用于构建特殊向量，表示从给定值开始每次增加给定值直到大于最大值，有格式：

v = [start[:step=1]:end]

例如，我们创建一个从 2 开始，间隔为 3 ，最后一个值恰好小于 6 的向量 [2 5]

e = 2:3:6

创建均匀分布的向量

linspace(x1,x2,N) 	 % 创建一个 N 个元素的向量，从 x1 开始，到 x2 结束

 

向量函数

函数	作用	函数	作用
max	求最大值	mean	求平均值
min	求最小值	median	求中间值
sum	求和	prod	乘积
length	求长度	sort	从小到大排序

 

访问元素

通过 () 来访问元素，注意下标从 1 开始，例如

a = [1 5 6 -3 8];

则 a(3) 就是 6 ；另外，可以利用 : 取向量切片：

a(1:2:5);

使用规则与之前相同，这里返回 [1 5 -3]

 

向量运算

加法、减法遵循向量的运算，但是其余运算有特殊格式：

dot(a, b)		 % 内积 
cross(a, b) 	 % 外积 

.表示两个向量的元素一对一地进行运算，因此当需要计算向量元素依次运算时，可以利用 .*、./、.^ 算符对每个元素分别操作

a = [1 2 3];
b = [1 2 3];
a.*b => [1 4 9]
a.^b => [1 4 27]

 

创建矩阵

函数	矩阵
[ ]	空矩阵
zeros(M,N)	创建一个 M x N 的全零矩阵
ones(M,N)	创建一个 M x N 的全一矩阵
eye(M)	创建一个 M x M 的单位矩阵
rand(M,N)	创建一个 M x N 的矩阵，元素为 0 ~ 1 随机值
randn(M,N)	创建一个 M x N 的矩阵，元素为满足标准正态分布
randi([a,b],M,N)	创建 [a,b] 范围的 M X N 随机矩阵
compan(A)	创建 A 的伴随矩阵
diag(a)	创建对角元为向量 a 元素的对角阵

 

矩阵运算

加法、减法、乘法遵循矩阵的运算，但除法有所不同：

• 左除 \ 表示将 A 的逆乘在左边 A\b
• 右除 / 表示将 A 的逆乘在右边 A/b

 

转置矩阵

利用上引号 ' 来进行转置操作，例如

A = [1 2 3]
A' = [1 2 3]^T

下面列举常用的函数

函数	作用	函数	作用
inv	矩阵的逆	det	矩阵行列式
trace	矩阵的迹	flipud	上下翻转
fliplr	左右翻转	diag	取对角向量
tril	取下三角	triu	取上三角
cond	矩阵条件数	norm	矩阵范数或模
rank	矩阵的秩	size	返回各维度上元素的数量

 

字符串

octave 中直接可以定义字符串，并且可以用单/双引号表示字符串

a = "hello"
b = 'hello'

下面是字符串相关函数

函数	作用	函数	作用
size	查看字符数组维数	deblank	删除字符串中的空格
char	把数字转换为字符串	strmatch	查找匹配字符串
strcmp	比较字符串	strjust	对齐字符数组
strcat	字符串连接	findstr	在字符串中找字符串
upper	转换为大写	lower	转换为小写

 

运算符

关系运算

关系运算符有 == >= <= > < ~= ，注意其中 ~= 表示不等于；如果关系成立结果为 1 ，否则结果为 0 。

 

逻辑运算

逻辑运算符有 & | ~ 表示或、与、非；另外使用 xor 表示异或

xor(1, 0);

 

数值计算

计时方法

% 开始计时
tic

% 需要计时的部分
...

% 停止计时
time = toc;

disp(time);
fprintf('Time = %3.2f',time);

 

函数求导

定义函数

syms x y z 		% 表示用 x y z 作为变量
u = x^2+y^2;	% 定义函数

函数取值 u(1,2,z) 得到一个 z 的函数

subs(u,x,y,1,2);

使用 disp 输出

disp(subs(u,x,y,1,2));

 

函数求偏导

函数	含义
diff(u,x)	u 对 x 求偏导
diff(u,x,2)	u 对 x 求 2 阶偏导

求得结果可以在给定点取值。注意它不能取得数值，只能取得表达式，因此给定值的个数不能超过未知数的个数

subs(diff(u,x),x,y,1,2); % 在 x = 1, y = 2 取值

只带其中一个变量的值

subs(diff(u,x),x,1);	% 在 x = 1 取值

最后会得到有关 y 的函数或者可以直接得到函数的 Jacobi 矩阵：

J = jacobian(u,[x y]);

 

数值求导

Matlab 没有内置直接计算数值求导的函数，只能把求导转化为差分格式。例如已知横坐标向量 x 和对应的函数值向量 y ，则导数向量可以被估计为

diff(y)./diff(x);

对于求梯度的时候， Matlab 有内置的函数，例如求 \(u=x^2y^3\) 在点 \((1,-2)\) 处的梯度

x = -3:0.2:3;	  % 将函数在一个 x y 的二维矩阵中离散
y = x'; 		 % 这里 y 做了转置

f = x.^2 ∗ y.^3;				% 计算函数的二维矩阵
[fx,fy] = gradient(f,0.2,0.2);	 % 求梯度

% 要找到 x = 1, y = -2 的那个点
x0 = 1;
y0 = -2;
% 判断表达式
t = (x == x0) & (y == y0);
% 寻找条件
indt = find(t);
% 查找满足坐标条件 x = 1, y = -2 的那个点的值
grad = [fx(indt) fy(indt)];

 

我们介绍其中的部分函数

gradient(F, dx, dy, ...);

它会求取矩阵 F 在不同方向上的梯度，默认每个方向的间隔为 1

x = gradient(F);

它会求出向量 F 的梯度向量 \(\partial F/\partial x\) ，默认间隔为 1

[x y] = gradient(F, 0.2, 0.2);

它会求出二维矩阵 F 的两个梯度向量 \(\partial F/\partial x\) 和 \(\partial F/\partial y\) ，每个方向间隔为 0.2

 

ind = find(X)

查找条件函数，找出矩阵 X 中的所有非零元素，并将这些元素的线性索引值（linear indices：按列）返回到向量 ind 中。如果 X 是一个行向量，则 ind 是一个行向量；否则，ind是一个列向量。

ind = find(X, k)

找到前 k 个不为 0 的线性索引值。 k 必须是一个正数，但是它可以是任何数字数值类型。

ind = find(X, k, 'last')

找到后 k 个不为零元素的线性索引值。

[row,col] = find(X, ...)

返回矩阵 X 中非零元素的行和列的索引值。这个语法对于处理稀疏矩阵尤其有用。如果 X 是一个N（N>2）维矩阵，col 包括列的线性索引。

需要注意， find 有精度要求，如果搜索精度过高会找不到，因此需要设定一个最小误差

t = (abs(x - x0) < 1e-5 & abs(y - y0) < 1e-5 );

 

求解线性方程组

设方程组形式为 \(Ax=b\) ，分为适定、超定、欠定三种情况讨论。

适定方程组

• inv(A)*b;

• A\b;

• [L,U] = lu(A); x = U\(L\b);

超定方程组

• A\b; 求得最小二乘解

• x = pinv(A)*b; 利用矩阵伪逆求解

欠定方程组：

• A\b; 求得最小二乘解

• x = pinv(A)*b; 利用矩阵伪逆求解

• 上面两种方法都只能求得一个特解，利用 null(A) 可以求得零空间，通过零空间的线性组合加特解可以得到通解

 

多项式

通过向量 \(p=[a_0,a_1,\cdots,a_n]\) ，多项式降幂排列系数数组可以直接构造多项式

poly2sym(p)

这个函数在 symbolic 包当中，需要手动安装

 

我们可以直接将数组当做一个多项式使用。通过将两个数组补充为相同长度，就可以通过数组加减进行多项式加减；还可以做乘法

p = conv(p1, p2)

返回相乘后得到的数组；以及带余除法

[p, r] = deconv(p1, p2)

返回商数组和余数数组；也可以进行积分和求导，同样返回结果数组

de = polyder(p);
in = polyint(p);

 

可以对多项式逐点求值，也可以利用函数转换为向量或矩阵

polyval(p, x)  			 % 单点求值
polyval(p, [x y]) 		 % 数组求值，返回向量
polyvalm(p, [x y; z w])   % 矩阵求值，返回矩阵

通过 roots 函数求多项式的所有根

roots(p)

最后给出两个暂时不用的函数：

polyeig	% 求解特征值问题
residue % 部分分式展开

 

插值函数

进行多项式插值

interp1(x, y, x1, 'method')

其中 x y 表示节点和对应的值，x1 是要插值的点，最终会返回 y1 ，表示插值多项式在 x1 处的值向量；最后一个参数选择插值方法：

method	作用
nearest	最近插值
linear	线性插值
spline	三次样条插值
cubic	三次插值

举一个例子：

interp1([1 2], [2 3], [1 1.5 2], 'linear')

注意 x1 不能超出 x 的范围。

 

曲线拟合函数

polyfit(x, y, n)

其中 x y 表示节点和对应的值， n 是多项式阶数，返回多项式系数和生成预测值误差估计的矩阵 s ，因此可以接收返回值

[p,s]= polyfit(x, y, n);

 

脚本

Octave 脚本是普通的文本文件，但需要以 .m 为后缀

 

调用脚本的命令有：

edit 调出编辑器来编辑脚本

edit name 编辑已有脚本

run name 运行脚本

 

全局变量

无论在脚本文件还是在函数文件中，都会定义一些变量。函数文件所定义的变量是局部变量，这些变量独立于其他函数的局部变量和工作空间的变量，即只能在该函数的工作空间引用，而不能在其他函数工作空间和命令工作空间引用。

但是如果某些变量被定义成全局变量，就可以在整个工作空间进行存取和修改，以实现共享。因此，定义全局变量是函数间传递信息的一种手段。

global A B C

 

数学函数

函数	作用	函数	作用
sin(x)	正弦	asin(x)	反正弦
cos(x)	余弦	acos(x)	反余弦
tan(x)	正切	atan(x)	反正切
cot(x)	余切	acot(x)	反余切
abs(x)	绝对值	max(x)	最大值
min(x)	最小值	sum(x)	求和
sqrt(x)	开平方	exp(x)	以 e 为底的指数
log(x)	自然对数	log10(x)	以 10 为底的对数
sign(x)	符号函数	fix(x)	取整
ceil(x)	向上取整	floor(x)	向下取整

 

输入输出

input()			% 输入函数
disp(); 	 	% 输出函数

例如：

x = input('请输入数据：');
disp(x);

 

还可以格式化输出结果

fprintf(format, ...);

使用方法和 C 语言中的 printf 类似。

 

载入和保存

save name 				 % 保存一个指定名称的命名空间（当前所有变量储存在其中）
save name var1 var2 ...   % 保存包含这些变量的命名空间
load name 				 % 载入一个指定名称的命名空间

 

可以从其它文件中载入数据

x = load('test.txt');

 

条件语句

if condition1
% code
elseif condition2
% code
else
% code
end

 

循环语句

for n = n1:step:n2
% code
end

 

while condition
% code
end

 

循环控制语句

break 结束当前循环

continue 跳过本次循环

return 返回

pause 程序暂停直到键盘响应；可以用 pause(n) 指定暂停的秒数

 

函数

用户可以自定义函数， octave 函数通过值传递并能返回多个返回值，按如下格式定义函数：

function[输出1, 输出2, ...] = name(输入1, 输入2, ...)
% code
end

例如我们可以定义计算 sin 的函数

function s=sind(x)
% SIND(x) Calculates sine(x) in degrees
s=sin(x*pi/180);
end

 

octave 中也有内联（inline）函数，例如将如下方程组：

\[\left\{\begin{aligned} &\sin x_1 + x_2 + x_3^2e^{x_1} - 4 = 0\\ &x_1 + x_2x_3 = 0\\ &x_1x_2x_3 = -2 \end{aligned}\right. \]

转化为下面的形式函数：

f = @(x) [sin(x(1)) + x(2) + x(3)^2*exp(x(1))-4; ...
x(1) + x(2)*x(3); x(1)*x(2)*x(3)+2];

这样就可以直接通过 f(x) 来调用该函数，返回一个结果向量；相当于求解该函数等于 [0 0 0] 的解。

 

绘图方法

图形窗口

通过 figure 来创建窗口

figure(n);	% 创建 n 号窗口

可以对创建的窗口进行操作

命令	作用
close	关闭当前窗口
close(n)	关闭指定窗口
close all	关闭所有窗口
clf	清空当前窗口

只需要点击一下窗口，就会自动把该窗口作为当前绘图窗口。

 

基本绘图函数

plot(x);			% x 的序号作为横坐标， x 值为纵坐标
plot(x, y); 		% 其中x, y分别为横纵坐标数据
subplot(a, b, c);    % 表示在一个格子中画图，分成axb的格子，在第c个格子里画图，其中格子的顺序为从左到右从上到下

可以对颜色和样式进行选择

• ro 代表红色圆圈
• b 代表蓝色点

plot(re(:, 1), re(:, 2), '.', 'MarkerSize', 20);
plot(re(:, 1), re(:, 2)./(re(:, 1).*log(re(:, 1))), '.');
plot(x, x.^2);	% 绘制y = x^2的图像
% 这表示将re分成re(:, 1)和re(:, 2)两个列向量

注意：由于这是向量运算，如果报错的话，尽量在每一个运算前加点'.'

 

plot 参数

• 曲线线型、颜色和标记点类型

plot(X1,Y1,LineSpec,...) % 通过字符串LineSpec指定曲线的线型、颜色及数据点的标记类型

% 注意：这些标识符写在一个字符串里
plot(x, y, '-b');

标识符	意义	标识符	意义
-	实线	+	加号
-.	点划线	x	叉号
--	虚线	r	红色
:	点线	g	绿色
.	点	b	蓝色
*	星号	y	黄色

 

• 设置曲线线宽、标记点大小，标记点边框颜色和标记点填充颜色

plot(..., 'Property Name', Property Value, ...);% 设置属性plot(x, y, '-b', 'MarkerSize', 20);

Property Name	意义	选项
LineWidth	线宽	数值，单位为points
MarkerEdgeColor	标记点边框线条颜色颜色字符	'g','b'等
MarkerFaceColor	标记点内部区域填充颜色颜色字符	'g','b'等
MarkerSize	标记点大小	数值，单位为points

具体参数的部分：https://blog.csdn.net/wzhw1992/article/details/26866491

 

• 同时绘制多条曲线

plot(x1, y1, 'style1', x2, y2, 'style2');

 

• 设置与保存

set(gca, 'FontSize', 20); 			% 设置字号
saveas(gcf, '文件名.xxx'); 		  % 输出为指定文件

 

• 更多函数

title() 	% 添加标题
xlabel() 	% 添加 x 轴名称
ylabel() 	% 添加 y 轴名称
legend() 	% 添加图例

 

• 在原图上继续绘制

plot(x, y);
hold on;
plot(x, y);

 

• 设置坐标轴

% 横纵坐标等比例
axis equal
% 设置横、纵坐标范围
axis([x1 x2, y1 y2]);

 

• 快速绘制曲线

linspace(a, b) 设置区间为a到b

x = linspace(-10, 10); % 设置 x 自变量为 -10 到 10
plot(x, sin(x)); 	   % 绘制 sinx 在 -10 到 10 的图像

 

• 三维绘图

绘制三维曲线的函数

plot3(x, y, z);

具体使用类似于 plot 函数；还可以绘制三维网格

mesh(x, y, z);

绘制三维曲面

surf(x, y, z);

 

直方图

使用 hist 函数绘制直方图，它有如下几种用法：

• 单一参数

hist(w);		% 绘制向量 w 的直方图

此时，向量 w 的数据范围作为横坐标的区间范围，然后从左向右将出现在该区间中的元素个数（频数）作为纵坐标

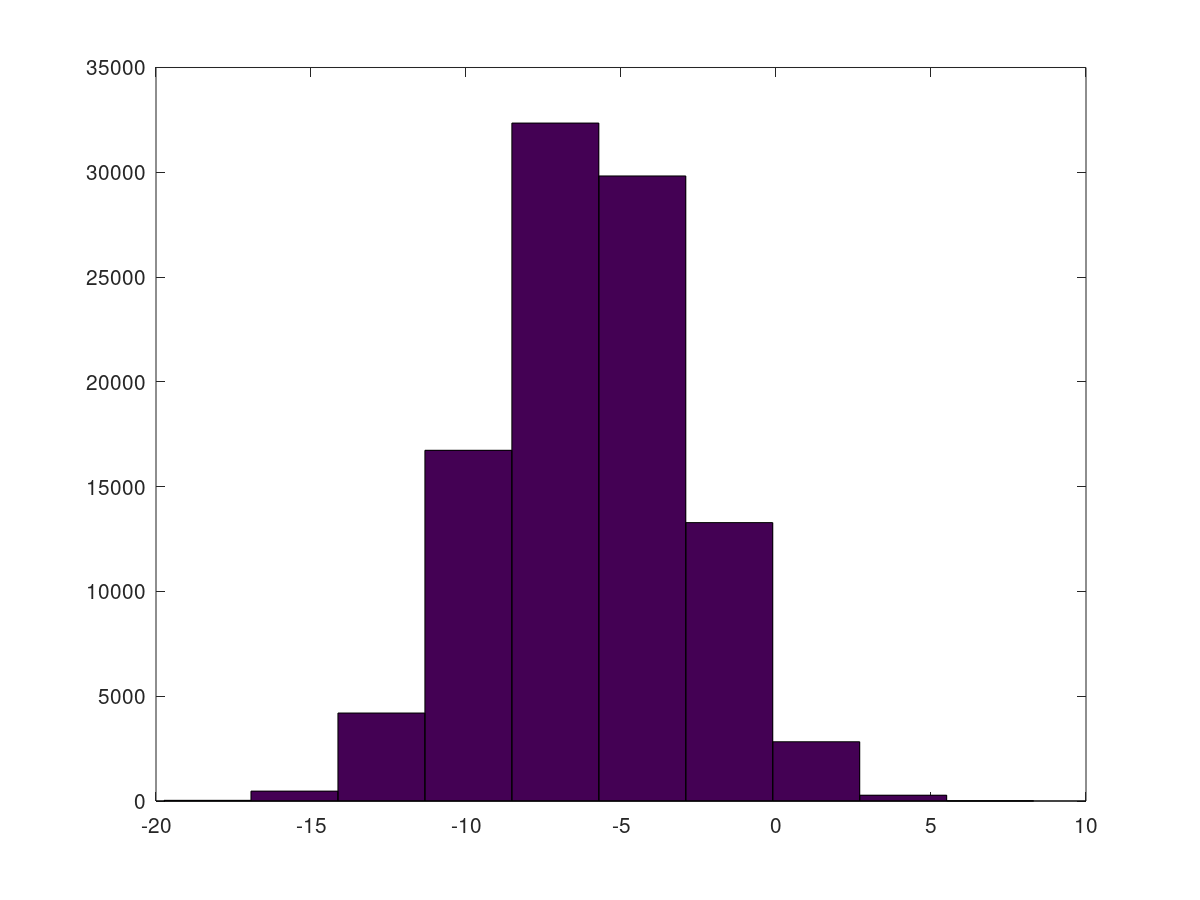
如图是一个 100000 维数组绘制的直方图，图中柱形的高度之和就是 100000 。

 

• 划分区间个数

hist(w, n);

可以指定将区间范围划分为 n 块，然后从左向右将出现在该区间中的元素个数（频数）作为纵坐标

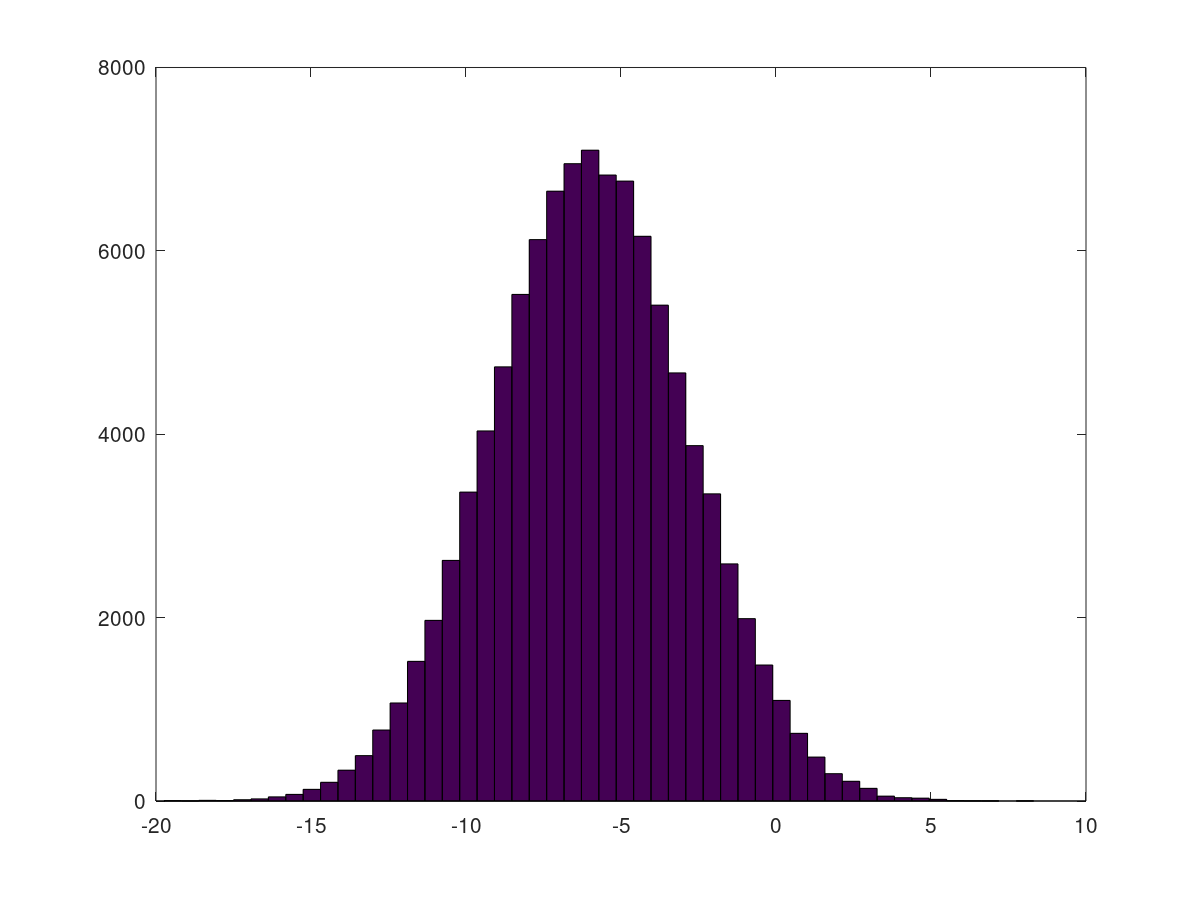
这是之前的 100000 维数组在 50 个区间上的频数直方图。

 

package

有时需要手动安装一些包，这时就需要使用 pkg 命令

pkg install -forge name

安装指定的 package ，然后加载 package

pkg load name