求解非线性方程
The bisection method
Algorithm 1.1. 二分法每次将区间减小一半,在其中有根的部分寻找连续函数 \(f:\mathbb{R}\to\mathbb{R}\) 的根.
Input: \(f:[a,b]\to\mathbb{R},\ a\in\mathbb{R},\ b\in\mathbb{R},\ M\in\mathbb{N}^+,\ \delta\in\mathbb{R}^+,\ c\in\mathbb{R}^+\)
Preconditions: \(f\in\mathcal{C}[a,b],\ \mathrm{sgn}(f(a))\neq \mathrm{sgn}(f(b))\)
Output: \(c,\ h,\ k\)
Postconditions: \(|f(c)|<\epsilon\) or \(|h|<\delta\) or \(k=M\)
// 二分法
double solve(double u, double v)
{
double u_f = f(u), v_f = f(v);
// 判断符号是否相同,如果相同,则退出
if (SIGN(u_f) == SIGN(v_f))
{
cout << "Same sign!" << endl;
return INFTY;
}
double mid, mid_f;
// 限制最多迭代 ITERATION 次
for (int i = 0; i < ITERATION; i++)
{
mid = (u + v) / 2;
mid_f = f(mid);
// 根据精度判断退出
if (fabs(u - v) < ACCURACY || fabs(u_f - v_f) < ACCURACY)
{
break;
}
// 根据端点符号选取区间
else if (SIGN(u_f) == SIGN(mid_f))
{
u = mid;
u_f = f(u);
}
else
{
v = mid;
v_f = f(v);
}
}
return mid;
}
Algorithm 1.9. 注意到每次循环,左端和右端符号都不变,因此只需要保存端点符号和区间长度,然后计算中间点的符号并与端点符号比较来选择区间,不需要保存端点的值.
Q-order convergence
Definition 1.10 (Q-order convergence). 收敛序列 \(\{x_n\}\) 称为是以 Q-order \(p\) \((p\ge 1)\) 收敛到 \(L\) ,若
常数 \(c\) 称为渐近因子 asymptotic factor ;特别的,当 \(p=1\) 时, \(\{x_n\}\) 有 Q-linear 收敛;当 \(p=2\) 时, \(\{x_n\}\) 有 Q-quadratic 收敛.
Definition 1.11. 序列 \(\{x_n\}\) 称为是线性收敛到 \(L\) ,若
收敛的阶是最大的 \(p\in\mathbb{R}^+\) ,满足
特别的,当 \(p=2\) 时, \(\{x_n\}\) 二阶收敛.
Theorem 1.12 (Monotonic sequence theorem). 单调有界序列收敛.
Theorem 1.13 (Convergence of the bisection method). 连续函数 \(f:[a_0,b_0]\to\mathbb{R}\) 满足 \(\mathrm{sgn}(f(a_0))\neq\mathrm{sgn}(f(b_0))\) ,则二分法序列线性收敛到根 \(\alpha\) 并且有渐近因子 \(\frac{1}{2}\) .
\(Proof.\) 收敛性显然;由 \(|c_n-\alpha|\le 2^{-(n+1)}(b_0-a_0)\) ,则有渐近因子 \(\frac{1}{2}\) .
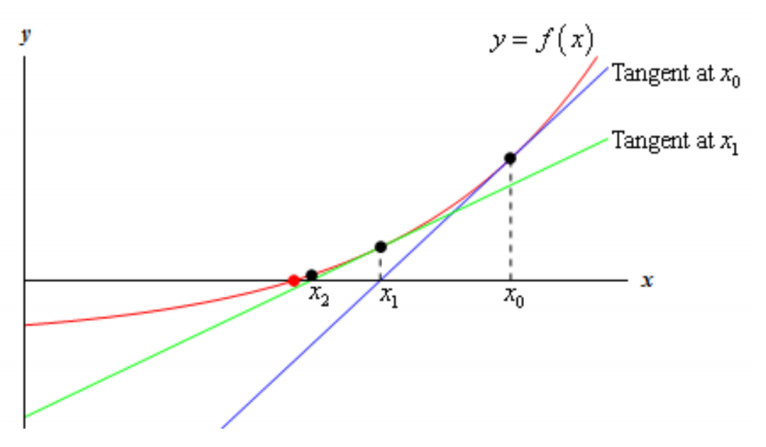
Newton's method
Algorithm 1.14. 牛顿法在初始位置 \(x_0\) 通过迭代公式
寻找连续函数 \(f:\mathbb{R}\to\mathbb{R}\) 的根.
Input: \(f:\mathbb{R}\to\mathbb{R},\ f^{\prime},\ x_0\in\mathbb{R},\ M\in\mathbb{N}^+,\ \epsilon\in\mathbb{R}^+\)
Preconditions: \(f\in\mathcal{C}^2\) 并且 \(x_0\) 足够接近 \(f\) 的根
Output: \(x,\ k\)
Postconditions: \(|f(x)|<\epsilon\) or \(k=M\)
// 牛顿法
double solve(double a, double b)
{
double dx, root = (b + a) / 2;
// 最多迭代 ITERATION 次
for (int i = 0; i < ITERATION; i++)
{
// 判断导函数是否为0
if (g(root) == 0)
{
cout << "Stop" << endl;
return root;
}
dx = f(root) / g(root);
// 误差精度小于 ACUURACY 则退出
if (fabs(dx) < ACCURACY)
{
break;
}
root -= dx;
}
return root;
}
Theorem 1.15 (Convergence of Newton's method). 连续函数 \(f:\mathcal{B}\to\mathbb{R},\ f\in\mathcal{C}^2,\ \mathcal{B}=[\alpha-\delta,\alpha-\delta]\) 满足 \(f(\alpha)=0,\ f^{\prime}(\alpha)\neq 0\) ,若选取 \(x_0\) 距离 \(\alpha\) 足够近,则牛顿公式中的迭代序列 \(\{x_n\}\) 至少二阶收敛到根 \(\alpha\) ,即
\(Proof.\) 在 \(x_n\) 处 Taylor 展开得
其中 \(\xi\) 在 \(\alpha\) 和 \(x_n\) 之间。代入 \(f(\alpha) = 0\) 有
由于 \(f^{\prime}\) 的连续性和 \(f^{\prime}(\alpha)\neq 0\) ,则
由最大最小值定理可定义
则当 \(x_0\) 离 \(\alpha\) 足够近时, \(|x_0-\alpha|=\delta_0<\delta_1\) ,并且 \(M\delta_0<1\) ,从而有
由于 \(M|x_0-\alpha|<1\) ,并且容易得到
从而 \(x_n\) 二次收敛到 \(\alpha\) .
Theorem 1.16. 连续函数 \(f:[a,b]\to[c,d]\) 是双射当且仅当它是严格单调的.
Theorem 1.17 若 \(\mathcal{C}^2\) 函数 \(f:\mathbb{R}\to\mathbb{R}\) 满足 \(f(\alpha)=0,\ f^{\prime}>0,\ f^{\prime\prime}>0\) ,则 \(\alpha\) 是 \(f\) 唯一的根,并且 \(\forall x_0\in\mathbb{R}\) ,牛顿迭代序列 \(\{x_n\}\) 二阶收敛到 \(\alpha\).
\(Proof.\) 由于 \(f\) 连续且严格单调,因此是双射。显然 \(\alpha\) 是唯一的根,且有
则由 \(f^{\prime}>0,\ f^{\prime\prime}>0\) 有 \(RHS>0\) ,因此 \(x_{n+1}-\alpha > 0\) ,这意味着 \(f(x_n)>f(\alpha)=0,\ \forall n>0\) , 根据迭代公式有
可以看到 \(\{x_n-\alpha :n>0\}\) 是单调递减的,因此是收敛的。不妨设 \(x_n\) 收敛到 \(a\) ,则
由于 \(\alpha\) 是唯一的根,只能有 \(a = \alpha\) .
Definition 1.18 令 \(\mathcal{V}\) 是向量空间,子集 \(\mathcal{U}\subseteq \mathcal{V}\) ,是凸集 convex set 当且仅当
函数 \(f:\mathcal{U}\to\mathbb{R}\) 是凸函数当且仅当
特别的,称 \(f\) 是严格凸函数,当上述 \(\le\) 替换为 \(<\) .
The secant method
Algorithm 1.19. 割线法在初始位置 \(x_0\) 通过迭代公式
寻找连续函数 \(f:\mathbb{R}\to\mathbb{R}\) 的根.
Input: \(f:\mathbb{R}\to\mathbb{R},\ x_0\in\mathbb{R},\ x_1\in\mathbb{R},\ M\in\mathbb{N}^+,\ \delta\in\mathbb{R}^+,\ \epsilon\in\mathbb{R}^+\)
Preconditions: \(f\in\mathcal{C}^2;\ x_0,\ x_1\) 足够接近 \(f\) 的根
Output: \(x_n,\ x_{n-1},\ k\)
Postconditions: \(|f(x_n)|<\epsilon\) or \(|x_n-x_{n-1}|<\delta\) or \(k = M\)
// 割线法
double solve(double x_0, double x_1)
{
double dx;
// 最多迭代 ITERATION 次
for (int i = 0; i < ITERATION; i++)
{
// 分母为0,退出
if (f(x_1) - f(x_0) == 0)
{
cout << "Stop" << endl;
return x_1;
}
dx = f(x_1) * (x_1 - x_0) / (f(x_1) - f(x_0));
// 根据精度判断是否退出
if (fabs(dx) < ACCURACY || fabs(x_1 - x_0) < ACCURACY)
{
break;
}
double tmp = x_1;
x_1 -= dx;
x_0 = tmp;
}
return x_1;
}
Definition 1.20. 斐波那契数列 Fibonacci numbers \(\{F_n\}\) 定义为
Theorem 1.21 (Binet's formula). 黄金比例 \(r_0 = \frac{1+\sqrt{5}}{2}\) ,令 \(r_1 = 1-r_0 = \frac{1-\sqrt{5}}{2}\) ,则
\(Proof.\) 我们定义
因此有 \(\mathbf{u}_n = A^n\mathbf{u}_0\) ,则有
注意到 \(A\) 的特征值为 \(r_0,\ r_1\) ,分别对应特征向量 \(\mathbf{x}_0 = (r_0,1)^T\) 和 \(\mathbf{x}_1 = (r_1,1)^T\) ;我们将初始向量 \(\mathbf{u}_0\) 表示为特征向量的线性组合
从而有
其中第二个分量的等式就是要求的结果.
Corollary 1.22. 比例 \(r_0,\ r_1\) 满足
\(Proof.\) 代入通项公式容易验证.
Lemma 1.23 (Error relation of the secant method). 在割线法中,存在 \(\xi_n\) 处于 \(x_{n-1}\) 与 \(x_n\) 之间,以及 \(\zeta_n\) 处于 \(\min(x_{n-1},x_n,\alpha)\) 与 \(\max(x_{n-1},x_n, \alpha)\) 之间,使得
\(Proof.\) 定义差分为
观察割线法的右边式子,利用 \(f(\alpha)=0\) 可以将割线法迭代公式写为
由中值定理存在 \(\xi_n\) 处于 \(x_{n-1}\) 与 \(x_n\) 之间,使得
定义函数 \(g(x) = f[x,x_n]\) ,再对 \(g(x)\) 应用中值定理,存在 \(\beta\) 在 \(x_{n-1}\) 和 \(\alpha\) 之间,使得
并且有
注意到 Taylor 展开
带回并计算 \(g^{\prime}(\beta)\) 得
其中 \(\zeta_n\) 处于 \(\min(x_{n-1},x_n,\alpha)\) 与 \(\max(x_{n-1},x_n, \alpha)\) 之间.
Theorem 1.24 (Convergence of the secant method). 考虑 \(\mathcal{C}^2\) 函数 \(f:\mathcal{B}\to\mathbb{R},\ \mathcal{B} = [\alpha-\delta, \alpha+\delta]\) 满足 \(f(\alpha) = 0,\ f^{\prime}(\alpha)\neq 0\) ,若选取 \(x_0,\ x_1\) 足够接近根 \(\alpha\) 且 \(f^{\prime\prime}(\alpha)\neq 0\) ,则割线法迭代序列 \(\{x_n\}\) 以阶 \(p = \frac{1+\sqrt{5}}{2}\) 收敛到根 \(\alpha\) .
Corollary 1.25. 考虑在根 \(\alpha\) 附近求解 \(f(x)=0\) 。令 \(m\) 和 \(sm\) 为计算 \(f(x)\) 和 \(f^{\prime}(x)\) 的时间,则通过牛顿法和割线法达到精度 \(\epsilon\) 所需的时间满足
其中 \(r_0 = \frac{1+\sqrt{5}}{2},\ c = \left|\frac{f^{\prime\prime}(\alpha)}{2f^{\prime}(\alpha)}\right|\) ,
\(Proof.\) 通过精度分析可证,但有些繁琐,证明省略.
Fixed-point iterations
Definition 1.26. 函数 \(g\) 的不动点 fixed point 是一个满足 \(g(\alpha) = \alpha\) 的独立参数.
Lemma 1.28. 若 \(g:[a,b]\to[a,b]\) 是连续的,则 \(g\) 在 \([a,b]\) 上至少有一个不动点.
\(Proof.\) 函数 \(f(x) = g(x) - x\) 满足 \(f(a)\ge 0,\ f(b)\le 0\) ,由连续函数的介值定理 \(f(x)\) 在 \([a,b]\) 上有根,即证.
Theorem 1.30 (Brouwer's fixed point). 任意连续函数 \(f:\mathbb{D}^n\to\mathbb{D}^n\) 其中
有一个不动点.
Definition 1.33. 不动点迭代 fixed-point iteration 是寻找 \(g\) 的不动点的公式方法,具有形式
Definition 1.36. 函数 \(f:[a,b]\to[a,b]\) 是 \([a,b]\) 上的压缩映射 contraction / contractive mapping 如果
Theorem 1.38 (Convergence of contractions). 若 \(g(x)\) 是 \([a,b]\) 上的连续压缩函数,则它有唯一不动点 \(\alpha\) ,使得对任意 \(x_0\in[a,b]\) 的不动点迭代收敛到 \(\alpha\) 且有
\(Proof.\) 由 Lemma 1.28 , \(g\) 有不动点。不妨设有两个不动点 \(\alpha,\ \beta\) ,则 \(|\alpha-\beta|=|g(\alpha)-g(\beta)|\le \lambda|\alpha-\beta|\) ,从而 \(\alpha = \beta\) ;在不动点迭代中,我们有
通过三角不等式和归纳得到
当 \(n=0\) 时,有 \(|x_0-\alpha|\le \frac{1}{1-\lambda}|x_1-x_0|\) ,代回上式即证.
Theorem 1.39. 考虑 \(g:[a,b]\to[a,b]\) ,若 \(g\in\mathcal{C}^1[a,b]\) 并且 \(\lambda = \max_{x\in[a,b]}\left|g^{\prime}(x)\right|<1\) ,则 \(g\) 有唯一不动点 \(\alpha\) ,使得对任意 \(x_0\in[a,b]\) 的不动点迭代收敛到 \(\alpha\) ,则 Theorem 1.38 成立,以及
\(Proof.\) 很容易通过主值定理证明 \(g\) 是连续压缩函数,从而 Theorem 1.38 成立。由于存在 \(\xi\) 在 \(x_n\) 与 \(\alpha\) 之间,使得
令 \(n\to\infty\) ,则有 \(g^{\prime}(\xi_n)\to g^{\prime}(\alpha)\) ,即证.
Corollary 1.40. 令 \(\alpha\) 为 \(g:\mathbb{R}\to\mathbb{R}\) 的不动点,且有 \(\left|g^{\prime}(\alpha)\right|<1\) 以及 \(g\in\mathcal{C}^1(\mathcal{B}),\ \mathcal{B} = [\alpha-\delta,\alpha+\delta],\ \delta>0\) ,若选取 \(x_0\) 足够接近 \(\alpha\) ,则 Theorem 1.38 成立.
\(Proof.\) 利用连续性取 \(\alpha\) 的邻域,使得 \(|g^{\prime}(x)|<1\) ,即证.
Corollary 1.41. 考虑 \(g:[a,b]\to[a,b]\) ,若有不动点 \(g(\alpha) = \alpha\in[a,b]\) ,则 \(x_0\) 足够接近 \(\alpha\) 的不动点迭代以 \(p\) 阶 \((p>1,\ p\in\mathbb{N})\) 收敛到 \(\alpha\) ,当
\(Proof.\) 由 Corollary 1.40 以及 \(g^{\prime}(\alpha) = 0\) ,不动点迭代唯一收敛。在 \(\alpha\) 处 Taylor 展开,存在 \(\xi\in[a,b]\) ,使得
由 \(g^{(p)}\) 的连续性,则它在 \([a,b]\) 上有界,从而由常数 \(M\) ,满足 \(E_{abs}(x_{n+1}) < ME_{abs}^p(x_{n})\) .
Problem
\(\mathrm{I}.\) 考虑二分法在区间 \([1.5,3.5]\) 上作用
- 第 \(n\) 步区间的宽度
故有第 $ n $ 步间隔为 $ 2^{-n}(3.5-1.5) = 2^{1-n}$ .
- 根 \(r\) 与区间中点距离的上确界
这里上确界不一定能到达.
\(\mathrm{II}.\) 在 \(a_0>0\) 的初始区间 \([a_0,b_0]\) 上应用二分法,则满足相对精度不大于 \(\epsilon\) 的 \(n\) 有
\(Proof.\) 设 $ \alpha $ 为根,需要 $ \frac{|c_n-\alpha|}{\alpha}\le\epsilon$ ,其中 $ c_n = (a_n+b_n)/2$ ,则有
其中使用了放缩 \(\alpha \ge a_0\) ,则有
即证.
\(\mathrm{IV}.\) 考虑在 \(x_0\) 应用牛顿法,则有 \(C\) 和 \(s\) 使得
其中 \(e_n\) 为牛顿法第 \(n\) 步的误差, \(s\) 为常数, \(C\) 依赖 \(x_n,\ f,\ f^{\prime}\) .
\(Proof.\) 对 $ f(\alpha) $ 泰勒展开则有
由于 \(e_n = |x_n-\alpha|\) ,则有
即有
即证.
\(\mathrm{V}.\) 在 \(\left(-\frac{\pi}{2},\frac{\pi}{2}\right)\) 上,迭代序列 \(x_{n+1} = \tan^{-1} x_n\) 是否收敛?
令 \(g(x) = \arctan x\) ,先说明它是连续压缩映射,这由
得到;由 Theorem 1.38 即证收敛到 \(\alpha\in\left[-\frac{\pi}{2},\frac{\pi}{2}\right]\) ,但显然两个端点不是收敛点,因此在上 \(\left(-\frac{\pi}{2},\frac{\pi}{2}\right)\) 收敛.
\(\mathrm{VI}.\) 令 \(p>1\) ,证明分数
是收敛序列.
\(Proof.\) 可得递推式
我们得到迭代函数
说明它是连续压缩映射,首先有
设 \(x_1 = \frac{1}{p},\ x_2=\frac{1}{1+\frac{1}{p}}\) ,则可将函数迭代的定义域改为
其中左端点是由于 \(g(x)<\frac{1}{p}\) ,代入这一最大值得到的下界,从而它是连续压缩映射,迭代序列收敛到 \(\alpha\) ,有
即证.
\(\mathrm{VII}.\) 若在 \(\mathrm{II}\) 中有 \(a_0<0<b_0\) 则会出现什么情况?考虑类似的估计.
设 $ \alpha \neq 0$ 为根,需要 $ \frac{|c_n-\alpha|}{\alpha}\le\epsilon$ ,其中 $ c_n = (a_n+b_n)/2$ ,则有
由于跨过了原点,无法放缩
注意到当 \(\alpha\) 非常靠近 \(0\) 时,相对误差会非常大,因此无法准确测量.


