数字信号处理实验（六）——FIR滤波器的设计

一、四种线性相位FIR滤波器的振幅响应

1、自编函数

[Hr,w,a,L]=hr_type1(h)（P256）  % h偶对称，N为奇数，h(n)=h(N-1-n)
[Hr,w,a,L]=hr_type2(h) （P257） % h偶对称，N为偶数，h(n)=h(N-1-n)
[Hr,w,a,L]=hr_type3(h) （P257） % h奇对称，N为奇数,h(n)=-h(N-1-n)
[Hr,w,a,L]=hr_type4(h) （P257） % h奇对称，N为偶数,h(n)=-h(N-1-n)

2、一个demo

clear all;close all;clc
addpath(genpath(pwd)); % 添加当前文件夹下所有路径

%% 
% 题1． 线性相位 FIR 滤波器的特性：
%% (2)已知滤波器的系统函数如下所示，用以上已编好的函数，确定滤波器的振
% 幅响应Hr(w)以及零点位置：
h1_n = [-4,1,-1,-2,5,6,5,-2,-1,1,-4];     % 偶对称,N=11
h2_n = [-4,1,-1,-2,5,6,6,5,-2,-1,1,-4];   % 偶对称,N=12
h3_n = [-4,1,-1,-2,5,0,-5,2,1,-1,4];      % 奇对称,N=11
h4_n = [ -4,1,-1,-2,5,6,-6,-5,2,1,-1,4];  % 奇对称,N=12

new_figure('线性相位FIR滤波器');
subplot(2,2,1);
[Hr,w]=hr_type1(h1_n);
plot(w/pi, abs(Hr));
title('第一类线性相位滤波器');
xlabel('w/pi');

subplot(2,2,2);
[Hr,w]=hr_type2(h2_n);
plot(w/pi, abs(Hr));
title('第二类线性相位滤波器');
xlabel('w/pi');

subplot(2,2,3);
[Hr,w]=hr_type3(h3_n);
plot(w/pi, abs(Hr));
title('第三类线性相位滤波器');
xlabel('w/pi');

subplot(2,2,4);
[Hr,w]=hr_type4(h4_n);
plot(w/pi, abs(Hr));
title('第四类线性相位滤波器');
xlabel('w/pi');

 

二、窗函数法

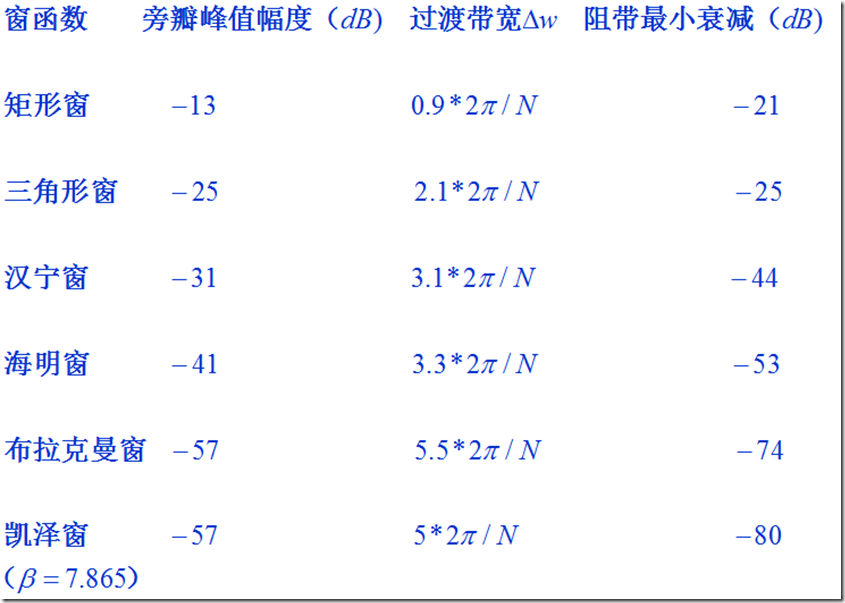
1、窗函数设计参考指标

2、窗函数设计方法一：

（1）根据实际阻带衰减指标，来确定所使用的窗函数。Matlab提供了几个函数来实现这些窗函数。

   W=boxcar(N);            % 矩形窗         －21dB
   W=triang(N);            % 三角窗         －25dB
   W=hanning(N);           % 汉宁窗         －44dB
   W=hamming(N);           % 海明窗         －53dB
   W=blackman(N);          % 布莱克曼窗     －74dB
   W=kaiser(N,beta);       % 凯泽窗         －80dB

（2）根据过渡带来计算出N值。

例： 通带截止频率wp, 阻带截止频率ws，已知为汉宁窗：N=3.1*2*pi/(ws-wp);

 

（3）求出理想的hd(n)。可使用ideal_lp（P185）来实现理想低通滤波器的冲激响应。

例：由ideal_lp来实现理想带阻滤波器的冲激响应。

hd=ideal_lp(wc1,N)+ideal_lp(pi,N)-ideal_lp(wc2,N);

 

（4）求得所设计的FIR滤波器的单位抽样响应:

h=hd.*w

 

（5）一个demo：

clear all;
wp=0.2*pi;
Rp=0.25;
ws=0.3*pi;
As=50;

wd = ws-wp;

N = ceil(6.6*pi/wd);
wn = (wp+ws)/2;

%
hd = ideal_lp(wn,N+1);
w_ham=(hamming(N+1))';
h = hd.*w_ham;
figure(2)
freqz(h,1,512)

 

 

3、窗函数设计方法二：

（1）根据实际阻带衰减指标，来确定所使用的窗函数。

（2）根据过渡带来计算出N值。

（3）利用Matlab所提供的函数fir1，来实现fir滤波器。

h=fir1(N,wn,’ftype’,windows(N+1))

›对于高通滤波器和带阻滤波器，N必须为偶数，N+1为奇数

›‘ftype’指的是：’low’,’bandpass’,’high’,’stop’

›设计的滤波器为N阶

（4）一个demo

%example6.2.3
clear all;
wp=0.2*pi;
Rp=0.25;
ws=0.3*pi;
As=50;

wd = ws-wp;
N = ceil(6.6*pi/wd);
wn = (wp+ws)/2;
b=fir1(N,wn/pi,hamming(N+1));
figure(1)
freqz(b,1,512)

 

三、频率抽样法：

1、根据给定的N值和过渡点来求得Hd(k) 。

2、利用DFT反变换求的所需的h(n)。

h=real(ifft(H,N));

 

clear all;
N=40;
T1=0.5925;
T2=0.1099;

alpha=(N-1)/2;
l=0:N-1;
wl=(2*pi/N)*l;

hrs=[zeros(1,5),T2,T1,ones(1,7),T1,T2,zeros(1,9),T2,T1,ones(1,7),T1,T2,zeros(1,4)];
k1 = 0:floor((N/2-1));
k2 = floor(N/2)+1:N-1;
angh = [-alpha*(2*pi)/N*k1,0,alpha*(2*pi)/N*(N-k2)];
H=hrs.*exp(j*angh);
h=real(ifft(H,N));

figure()
freqz(h,1,512)
[db,mag,pha,grd,w]=freqz_m(h,1);
[hr,ww,a,L]=hr_type2(h);

figure()
subplot(2,2,1),stem(wl(1:21)/pi,hrs(1:21)),title('H(k)')
subplot(2,2,2),stem(l,h),title('冲激响应')
subplot(2,2,3),plot(ww/pi,hr);grid;title('幅度响应')
subplot(2,2,4),plot(w/pi,db),axis([0,1,-80,10]),grid,title('幅频响应(db)')