PAT 1127 ZigZagging on a Tree[难]

1127 ZigZagging on a Tree （30 分）

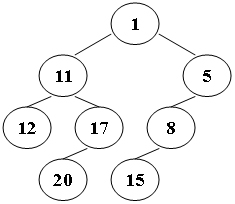
Suppose that all the keys in a binary tree are distinct positive integers. A unique binary tree can be determined by a given pair of postorder and inorder traversal sequences. And it is a simple standard routine to print the numbers in level-order. However, if you think the problem is too simple, then you are too naive. This time you are supposed to print the numbers in "zigzagging order" -- that is, starting from the root, print the numbers level-by-level, alternating between left to right and right to left. For example, for the following tree you must output: 1 11 5 8 17 12 20 15.

Input Specification:

Each input file contains one test case. For each case, the first line gives a positive integer N (≤30), the total number of nodes in the binary tree. The second line gives the inorder sequence and the third line gives the postorder sequence. All the numbers in a line are separated by a space.

Output Specification:

For each test case, print the zigzagging sequence of the tree in a line. All the numbers in a line must be separated by exactly one space, and there must be no extra space at the end of the line.

Sample Input:

8
12 11 20 17 1 15 8 5
12 20 17 11 15 8 5 1

Sample Output:

1 11 5 8 17 12 20 15

 题目大意：给出二叉树的中根遍历和后根遍历序列，给出zigzag遍历序列，就是隔层从左到右，从右到左这样转换遍历。

//这个我当然是不会了，好久没做二叉树的题目了。

转自：https://www.liuchuo.net/archives/3758

#include <iostream>
#include <vector>
#include <queue>
#include<cstdio>
using namespace std;
vector<int> in, post, result[35];
int n, tree[35][2], root;
struct node {
    int index, depth;//保存index和深度。
};
//将二叉树的结构存储在了tree中。
void dfs(int &index, int inLeft, int inRight, int postLeft, int postRight) {
    if (inLeft > inRight) return;
    index = postRight;//进来之后再赋值，真的厉害。
    int i = 0;
    while (in[i] != post[postRight]) i++;
    dfs(tree[index][0], inLeft, i - 1, postLeft, postLeft + (i - inLeft) - 1);
    dfs(tree[index][1], i + 1, inRight, postLeft + (i - inLeft), postRight - 1);
}
//dfs函数得到的root实际上是post遍历中的下标。
void bfs() {
    queue<node> q;
    q.push(node{root, 0});
    while (!q.empty()) {
        node temp = q.front();
        q.pop();
        result[temp.depth].push_back(post[temp.index]);
        if (tree[temp.index][0] != 0)//左子树不为空。
            q.push(node{tree[temp.index][0], temp.depth + 1});
        //那么此时push进的是左子树，并且深度+1.
        if (tree[temp.index][1] != 0)//右子树不为空。
            q.push(node{tree[temp.index][1], temp.depth + 1});
    }
}
int main() {
    cin >> n;
    in.resize(n + 1), post.resize(n + 1);
    for (int i = 1; i <= n; i++) cin >> in[i];//输入中序遍历
    for (int i = 1; i <= n; i++) cin >> post[i];//输入后序遍历
    dfs(root, 1, n, 1, n);//将根存在了root中。
    bfs();
    printf("%d", result[0][0]);
    for (int i = 1; i < 35; i++) {
        if (i % 2 == 1) {
            for (int j = 0; j < result[i].size(); j++)
                printf(" %d", result[i][j]);
        } else {
            for (int j = result[i].size() - 1; j >= 0; j--)
                printf(" %d", result[i][j]);
        }
    }
    return 0;
}

 

//柳神真厉害。

1.使用dfs在遍历的过程中传进去index引用参数，直接赋值，并且使用tree二维数组存储二叉树的结构

2.使用结构体node，存储下标和层数，下标是在post序列中可以寻到节点的。

3.对奇数层和偶数层，分别用不同的方式打印。

代码来自：https://www.cnblogs.com/chenxiwenruo/p/6506517.html

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <string.h>
#include <string>
#include <map>
#define LEFT 0
#define RIGHT 1
using namespace std;
const int maxn=35;
int inorder[maxn];
int postorder[maxn];
int level[maxn][maxn]; //每层的节点id
int levelcnt[maxn]; //每层的节点个数
int maxlayer=0;
int cnt=0; //节点id
struct Node{
    int left=-1,right=-1;
    int val;
}node[maxn];

//根据中序遍历和后序遍历建立树
void build(int inL,int inR,int postL,int postR,int fa,int LorR){
    if(inL>inR)
        return;
    int val=postorder[postR];
    int idx;
    //在中序遍历中找出父亲节点的索引，其左边是左子树，右边是右子树
    for(int i=inL;i<=inR;i++){
        if(inorder[i]==val){
            idx=i;
            break;
        }
    }
    int lnum=idx-inL;//左子树的节点个数
    cnt++;
    node[cnt].val=val;
    if(LorR==LEFT)
        node[fa].left=cnt;
    else if(LorR==RIGHT)
        node[fa].right=cnt;
    int tmp=cnt;
    build(inL,idx-1,postL,postL+lnum-1,tmp,LEFT);
    //这里的left标志是当前深度遍历中是左子树还是右子树。
    build(idx+1,inR,postL+lnum,postR-1,tmp,RIGHT);
}
void dfs(int root,int layer){
    if(root==-1)
        return;
    maxlayer=max(layer,maxlayer);
    level[layer][levelcnt[layer]]=root;
    levelcnt[layer]++;
    dfs(node[root].left,layer+1);
    dfs(node[root].right,layer+1);
}
int main()
{
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)
        cin>>inorder[i];
    for(int i=1;i<=n;i++)
        cin>>postorder[i];
    build(1,n,1,n,-1,-1);
    dfs(1,1);
    bool flag=true;
    printf("%d",node[1].val);
    for(int i=2;i<=maxlayer;i++){
        if(flag){
            for(int j=0;j<levelcnt[i];j++)
                printf(" %d",node[level[i][j]].val);
        }
        else{
            for(int j=levelcnt[i]-1;j>=0;j--)
                printf(" %d",node[level[i][j]].val);
        }
        flag=!flag;
    }
    return 0;
}

 

1.这个是使用函数建树，具体的代码理解在代码里。