Andrew Ng-ML-第十七章-推荐系统

1.问题规划

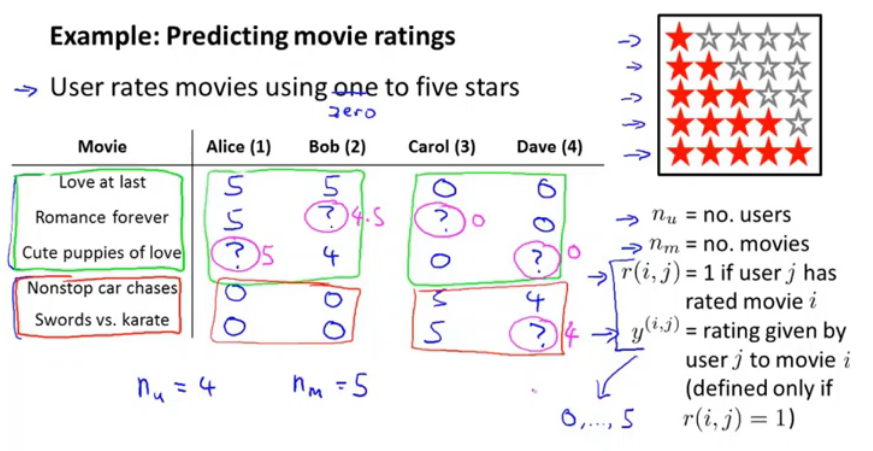
 图1.推荐系统在研究什么？

 例子：预测电影的评分。

 当知道n_u用户数,n_m电影数；r(i,j)用户j评价了电影i，那么就是1；y(i,j)如果r(i,j)为1，那么就给出评分。

 问题就是根据现有数据训练学习算法，预测未评分的电影。

 2.基于内容的推荐算法

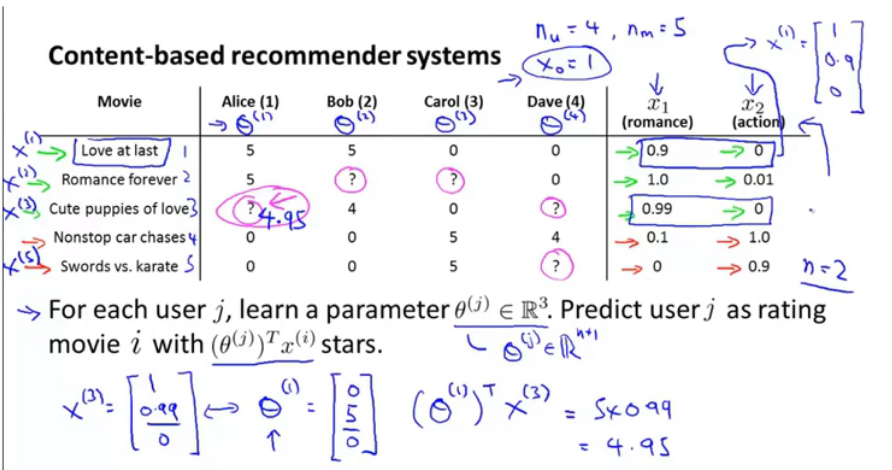
图2.基于内容的推荐系统

 对5部电影进行类型分析，有两个指标x_1,x_2,分别是爱情、动作，加上x_0之后形成指标。

从线性回归的角度来说，对每一个用户训练一个回归模型，每个用户都对应系数，对用户1Alice的参数[0,5,0]T，即对爱情片评分高，那么x电影参数输入后就得出大分为4.95.

图3.问题公式

 这里引入了代价函数公式，介绍了参数的含义，r(i,j)即是否已经评分，y(i,j)是如果评分的分数。

θ(j)是对用户j的参数，x(i)是电影i的特征向量，m(j)是评分电影的数量，并且公式加入了正则项。

在优化时，由于m(i)是常数，所以可以将其去掉，优化时仍能得到最优的theta_j。

图4.最优化算法

 第一个公式是对所有的参数进行求和并最小化，记作J(θ1，θ2，，，，θm)。

 梯度下降更新，当k=0，也就是常数项；当k≠0，即需要正则化非常数项。

基于内容的推荐算法是有一个前提的，就是电影的所有特征指标类型都是已知的，但是这通常不会很符合正常情况，下节介绍不是基于内容的推荐算法。

 3.协同过滤

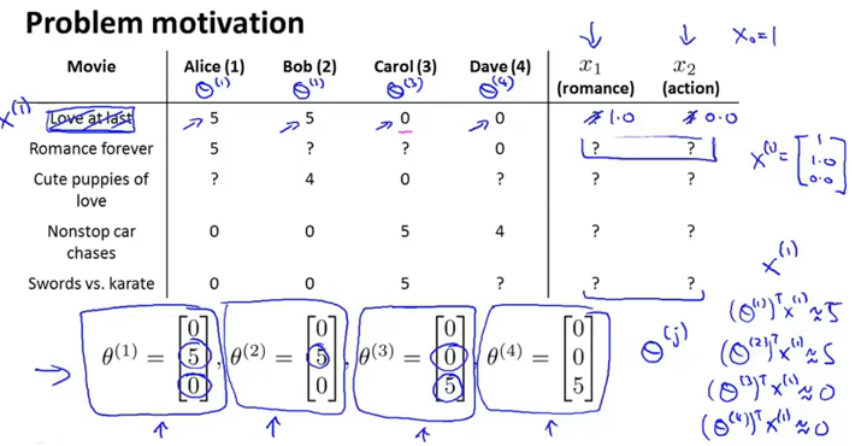
图5.问题动机

 由于电影的成分向量通常是不可得的，所以通过另一种方法来获取电影的成分向量。

假设用户给出了对爱情电影和动作电影的喜爱程度，即系数矩阵，那么根据评分，就可以得出对应的电影的成分向量特征。

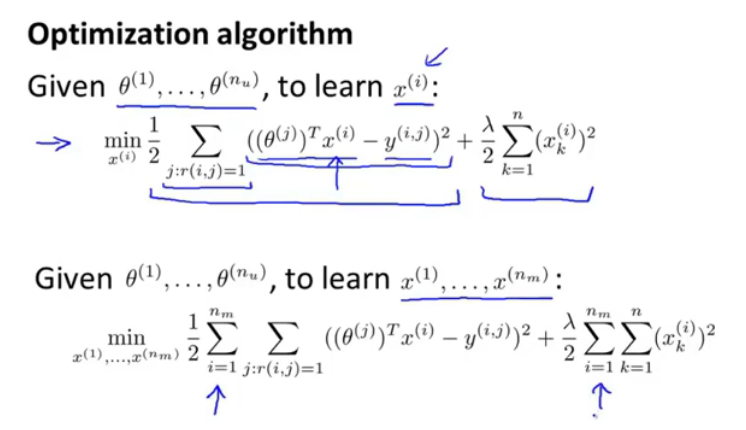
图6.最优化算法

 对一个电影求成分向量，通过最优化式1。

对n_m个电影求最优化，需要加上一个求和项，对n_m个电影的参数求和并最小化。

图7.协同过滤

 上节讲的是给定电影的成分向量和评分，可以预测出用户偏好向量。

本节讲的是给出用户偏好向量，可以估测出x_(1),,,,,电影的成分向量。

 那么就得出，首先通过随机初始化偏好向量，就可以根据对电影的已有评分预测出成分向量，那么再根据方法1，预测出偏好向量，以此类推，得到最终的优化结果。

4.协同过滤算法

图8.协同过滤最优化目标

 对式1中，前一项的求和是如果用户j评分了，那么就将某一用户对电影评分的分数求和。

对式2中，正好相反，是对一个电影来说，将所有用户评分求和。

式3是将其合并，作为一个最小化公式。

并且最后提到x和θ中不存在常数项，即1项，那么就是n维的，不是n+1维的。

图9.协同过滤算法

 1.首先初始化成分向量和用户偏好向量为较小的随机值。

 2.使用梯度下降法最小化代价函数，对i电影的第k个属性的更新公式，与对j用户对第k个电影的评分更新公式。

 3.对每个用户得出了参数θ，并且对一个电影学习到了特征向量x,那么就是已通过θTx来得到评分。

如用户j对电影i没有评分，那么就可以通过这个θTx来进行预测。

 5.矢量化：低秩矩阵分解

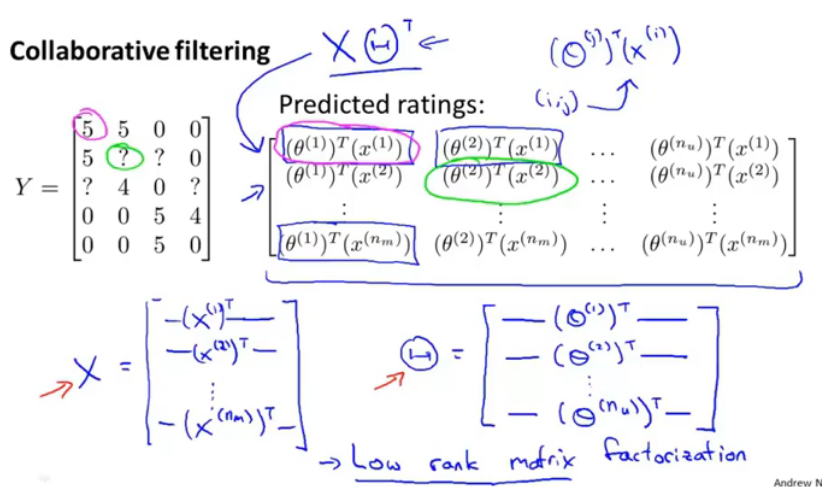
图10.低秩矩阵分解

将电影的评分作为矩阵Y，那么预测的评分就如右边大矩阵，其中列向量是一个用户对所有电影的评分，行向量是一个电影所有的评分。

那么如何进行简化呢？

首先将X矩阵表示为左下，θ矩阵表示为右下，那么整个大矩阵就可表示为 XθT。

图11.寻找相似电影

 那么如何向用户推荐相似电影呢？

根据电影的特征向量，找到5个与当前电影特征向量最小距离的，即为相似电影。也不只是电影，可以拓展到任何其他物品。

6.实施细节：均值规范化

图12.加入有用户从未评分

假设偏好向量中特征数为2，若Eve未对任一电影评分；

此时由于加入了正则化项，且式子前半部分没有对θ有所限制，所以会得到，Θ_(5)=0向量的结果。

那么此时就这个用户的评分预测就会产生误差。

需要使用均值归一化来解决问题。

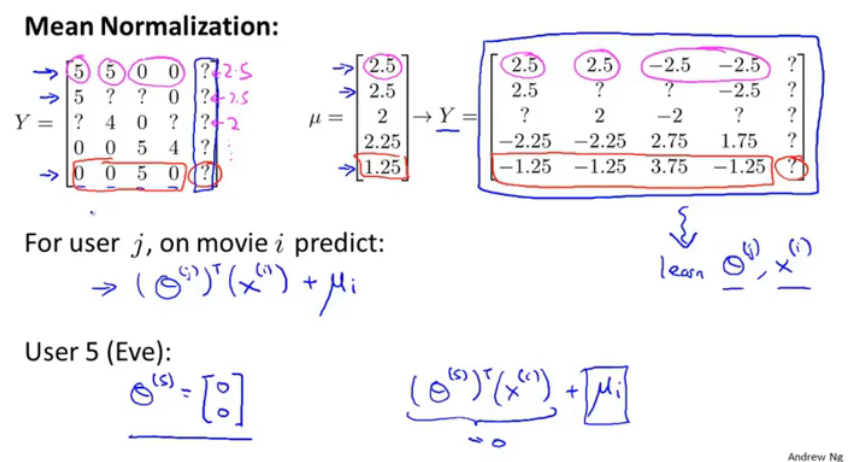
图13.均值归一化

 将电影评分形成矩阵，并按行求出没个电影的评分均值得到均值向量μ， Y-μ之后，得到新的均值矩阵。

在使用协同过滤算法训练出theta_j与x_i之后，在进行预测电影评分时，仍要+均值。

对于之前出现的问题，用户5得到的偏好向量仍然为0，但是现在加上了均值，就避免了评分全为0的现象，即根据电影的均值评分进行推送了。