scipy.optimize.minimize||非线性规划

https://blog.csdn.net/sinat_17697111/article/details/81534935

https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize.html

1.非凸函数的非线性规划

 非线性规划包括凸函数的和非凸函数的两种，minimize主要是针对非凸函数的 求极值的。

 

 2.minimize函数

 

 fun: 求最小值的目标函数

x0:变量的初始猜测值，如果有多个变量，需要给每个变量一个初始猜测值。

method:求极值的方法.

minimize是求局部最优解的。

 

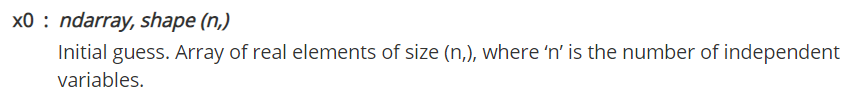
 x0是一个向量，可以存储多个输入进来的参数。

constraints可以给x0中对应的变量设置范围。

3.例子

# coding=utf-8
from scipy.optimize import minimize
import numpy as np
 
#demo 1
#计算 1/x+x 的最小值
def fun():
    v=lambda x:1/x[0] +x[0]
    #v=1/x0+x0#不能这么写
    return v
 
if __name__ == "__main__":
    x0 = np.asarray((2))  # 初始猜测值
    res = minimize(fun(), x0, method='SLSQP')
    print(res.fun)#这样来调用
    print(res.success)
    print(res.x)

#输出：
2.0000000815356342
True
[1.00028559]

 

如果初始化为3的话

if __name__ == "__main__":
    x0 = np.asarray((3))  # 初始猜测值
    res = minimize(fun(), x0, method='SLSQP')
    print(res.fun)#这样来调用
    print(res.success)
    print(res.x)

#输出：
-305175768.37511855
True
[-3.05175768e+08]

 

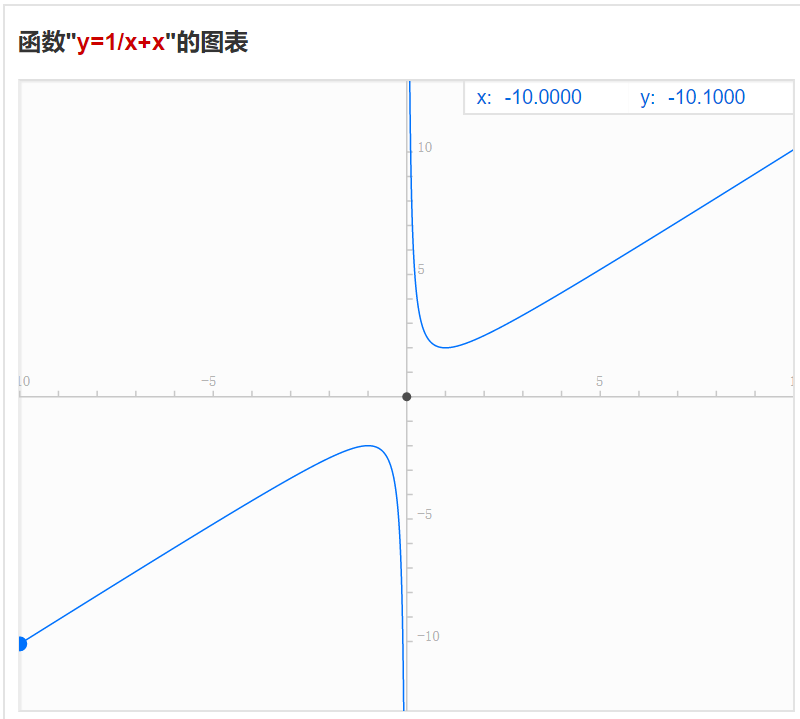
可以看到它计算出了新的极小值，该函数的图像，那能计算出负的这么大的，也是很神奇了。

4.返回的结果

from scipy.optimize import minimize
def fun():
    v=lambda x:1/x[0] +x[0]
    return v
coef=minimize(fun(),2)

#
>>> coef
      fun: 2.0
 hess_inv: array([[0.50030262]])
      jac: array([0.])
  message: 'Optimization terminated successfully.'
     nfev: 24
      nit: 6
     njev: 8
   status: 0
  success: True
        x: array([1.])

 

其中x就是取极小值时x的取值，可以通过

>>> coef['x']
array([1.])

 

获取到，用于其他计算。