LOJ#535. 「LibreOJ Round #6」花火
$n \leq 300000$的一个排列,每次能交换相邻两个数,并且有一次机会交换不相邻的两个数,可以不用这个机会。问使这个排列升序最少操作几次。
如果没有“不相邻”,那就是当年入门的时候学的逆序对了。也就是说,这次机会希望把逆序对数尽可能减少。把排列变成点放在二维平面上,$(i,a_i)$,可以发现交换$(i,a_i)$和$(j,a_j)$减少的答案,就是他们为端点的矩形里的点数(不含他们两个)的两倍,且必须$i>j,a_i<a_j$,否则就是答案变大这么多了。
进一步观察,如果有$k<j,a_k>a_j$,那么所有的交换$(j,i),j<i$都是不如交换$(k,i)$优的(前者的对应矩形被后者完全包含),因此左上端点一定在从$(1,a_1)$开始的一个递增序列(记为$L$)里。右下端点同理,一定在从$(n,a_n)$往前走的一个越走越小的序列(记为$R$)里,可以处理出来,但点的数量级是没变的。
法一:$R$中的点和$L$中的点配满足决策单调性。证明:如下图,$x,y$是$R$中的点,$p,q$是$L$中的点,如果在$x$处最优决策点是$q$,$S$表示一个区域里有几个点$(i,a_i)$,那么有$S_1>S_2+S_3$,那么在$y$处决策的时候,就有$S_1+S_4>S_2$,因此$p$还是不如$q$优。
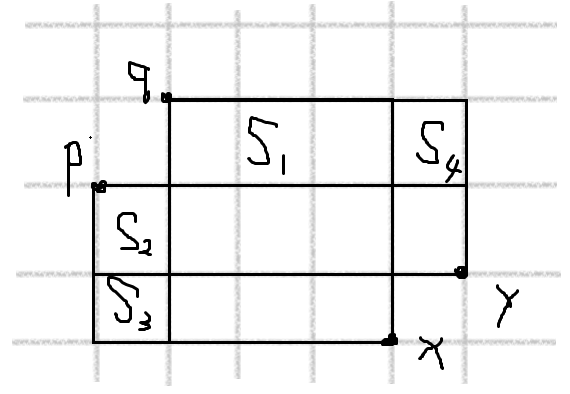
于是整体二分,用主席树计算矩形点数,俩log。

1 //#include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 //#include<time.h> 5 //#include<math.h> 6 //#include<set> 7 #include<queue> 8 //#include<bitset> 9 //#include<vector> 10 #include<algorithm> 11 #include<stdlib.h> 12 using namespace std; 13 14 #define LL long long 15 LL qread() 16 { 17 char c; LL s=0; int f=1; while ((c=getchar())<'0' || c>'9') (c=='-') && (f=-1); 18 do s=s*10+c-'0'; while ((c=getchar())>='0' && c<='9'); return s*f; 19 } 20 21 //Pay attention to '-' , LL and double of qread!!!! 22 23 int n; 24 #define maxn 300011 25 int a[maxn]; 26 struct BIT 27 { 28 int a[maxn],n; 29 void clear(int N) {n=N;} 30 void add(int x,int v) {for (;x<=n;x+=x&-x) a[x]+=v;} 31 int query(int x) {int ans=0; for (;x;x-=x&-x) ans+=a[x]; return ans;} 32 }t; 33 34 int root[maxn]; 35 struct SMT 36 { 37 struct Node{int ls,rs,sum;}a[maxn*20]; 38 int size,n; 39 void clear(int N) {n=N; size=0;} 40 void in(int &x,int y,int L,int R,int v) 41 { 42 x=++size; a[x].sum=a[y].sum+1; 43 if (L==R) return; 44 int mid=(L+R)>>1; 45 if (v<=mid) in(a[x].ls,a[y].ls,L,mid,v),a[x].rs=a[y].rs; 46 else in(a[x].rs,a[y].rs,mid+1,R,v),a[x].ls=a[y].ls; 47 } 48 void in(int &x,int y,int v) {in(x,y,1,n,v);} 49 int Query(int x,int L,int R,int ql,int qr) 50 { 51 if (ql<=L && R<=qr) return a[x].sum; 52 int mid=(L+R)>>1,ans=0; 53 if (ql<=mid) ans+=Query(a[x].ls,L,mid,ql,qr); 54 if (qr>mid) ans+=Query(a[x].rs,mid+1,R,ql,qr); 55 return ans; 56 } 57 int query(int x,int ql,int qr) {return Query(x,1,n,ql,qr);} 58 }tt; 59 60 int sl[maxn],tl,sr[maxn],tr; 61 int query(int x,int y) 62 { 63 x=sl[x]; y=sr[y]; 64 if (y<x || a[x]<a[y]) return 0; 65 int rx=root[x],ry=root[y-1]; 66 return tt.query(ry,a[y]+1,a[x]-1)-tt.query(rx,a[y]+1,a[x]-1); 67 } 68 69 int f[maxn]; 70 void solve(int pl,int pr,int L,int R) 71 { 72 if (L>R) return; 73 int mid=(L+R)>>1,id=0; 74 for (int i=pr,tmp;i>=pl;i--) if ((tmp=query(i,mid))>f[mid]) 75 { 76 f[mid]=tmp; 77 id=i; 78 } 79 solve(pl,id,L,mid-1); solve(id,pr,mid+1,R); 80 } 81 82 int main() 83 { 84 n=qread(); 85 for (int i=1;i<=n;i++) a[i]=qread(); 86 LL ans=0; t.clear(n); 87 for (int i=n;i;i--) 88 { 89 ans+=t.query(a[i]-1); 90 t.add(a[i],1); 91 } 92 93 tt.clear(n); 94 for (int i=1;i<=n;i++) tt.in(root[i],root[i-1],a[i]); 95 96 tl=tr=0; 97 for (int i=1;i<=n;i++) if (!tl || a[sl[tl]]<a[i]) sl[++tl]=i; 98 for (int i=n;i;i--) if (!tr || a[sr[tr]]>a[i]) sr[++tr]=i; 99 for (int i=1,to=tr>>1;i<=to;i++) sr[i]^=sr[tr-i+1]^=sr[i]^=sr[tr-i+1]; 100 101 solve(1,tl,1,tr); 102 int tmp=0; 103 for (int i=1;i<=tr;i++) tmp=max(tmp,f[i]); 104 ans-=tmp*2; 105 printf("%lld\n",ans); 106 return 0; 107 }
法二:以前做过扫描线:较少的矩形,很多的点,问一个点最多被多少矩形覆盖,现在是较多的矩形较少的点,问一个矩形最多覆盖多少点。从点对矩形的贡献入手实施转化:一个点$(x,a_x)$,设$l$是最小的$a_l>a_x$的数,$r$是最大的$a_r<a_x$的数,那么他对左端点在$[l,x-1]$,右端点在$[x+1,r]$的交换组$(i(左端点),j(右端点))$有贡献。新建平面,左端点为x轴,右端点为y轴,现在就变成了较少矩形较多点问一个点最多被多少矩形覆盖了。一个log。

1 //#include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 //#include<time.h> 5 //#include<math.h> 6 //#include<set> 7 #include<queue> 8 //#include<bitset> 9 //#include<vector> 10 #include<algorithm> 11 #include<stdlib.h> 12 using namespace std; 13 14 #define LL long long 15 LL qread() 16 { 17 char c; LL s=0; int f=1; while ((c=getchar())<'0' || c>'9') (c=='-') && (f=-1); 18 do s=s*10+c-'0'; while ((c=getchar())>='0' && c<='9'); return s*f; 19 } 20 21 //Pay attention to '-' , LL and double of qread!!!! 22 23 int n; 24 #define maxn 300011 25 int a[maxn]; 26 struct BIT 27 { 28 int a[maxn],n; 29 void clear(int N) {n=N;} 30 void add(int x,int v) {for (;x<=n;x+=x&-x) a[x]+=v;} 31 int query(int x) {int ans=0; for (;x;x-=x&-x) ans+=a[x]; return ans;} 32 }t; 33 34 struct SMT 35 { 36 struct Node{int ls,rs,add,Max;}a[maxn<<1]; 37 int size,n; 38 void build(int &x,int L,int R) 39 { 40 x=++size; 41 if (L==R) return; 42 int mid=(L+R)>>1; 43 build(a[x].ls,L,mid); build(a[x].rs,mid+1,R); 44 } 45 void clear(int N) {n=N; size=0; int x; build(x,1,n);} 46 int ql,qr,v; 47 void up(int x) {a[x].Max=max(a[a[x].ls].Max,a[a[x].rs].Max);} 48 void addsingle(int x,int v) {a[x].add+=v; a[x].Max+=v;} 49 void down(int x) {Node &b=a[x]; if (b.add) {addsingle(b.ls,b.add); addsingle(b.rs,b.add); b.add=0;} } 50 void Add(int x,int L,int R) 51 { 52 if (ql<=L && R<=qr) {addsingle(x,v); return;} 53 down(x); 54 int mid=(L+R)>>1; 55 if (ql<=mid) Add(a[x].ls,L,mid); 56 if (qr>mid) Add(a[x].rs,mid+1,R); 57 up(x); 58 } 59 void add(int L,int R,int V) {ql=L; qr=R; v=V; Add(1,1,n);} 60 }tt; 61 62 int sl[maxn],tl,sr[maxn],tr,pre[maxn],suf[maxn]; 63 struct Ope 64 { 65 int x,y1,y2,v; 66 bool operator < (const Ope &b) const {return x<b.x;} 67 }op[maxn<<1]; int lp=0; 68 69 int main() 70 { 71 n=qread(); 72 for (int i=1;i<=n;i++) a[i]=qread(); 73 LL ans=0; t.clear(n); 74 for (int i=n;i;i--) 75 { 76 ans+=t.query(a[i]-1); 77 t.add(a[i],1); 78 } 79 80 tl=tr=0; 81 for (int i=1;i<=n;i++) if (!tl || a[sl[tl]]<a[i]) sl[++tl]=i; 82 for (int i=n;i;i--) if (!tr || a[sr[tr]]>a[i]) sr[++tr]=i; 83 for (int i=1,to=tr>>1;i<=to;i++) sr[i]^=sr[tr-i+1]^=sr[i]^=sr[tr-i+1]; 84 85 for (int i=1;i<=n;i++) pre[i]=max(pre[i-1],a[i]); 86 suf[n]=a[n]; for (int i=n-1;i;i--) suf[i]=min(suf[i+1],a[i]); 87 for (int i=1;i<=n;i++) 88 { 89 int L=1,R=i; 90 while (L<R) 91 { 92 int mid=(L+R)>>1; 93 if (pre[mid]>a[i]) R=mid; 94 else L=mid+1; 95 } 96 int ll=L; 97 L=i,R=n; 98 while (L<R) 99 { 100 int mid=(L+R+1)>>1; 101 if (suf[mid]<a[i]) L=mid; 102 else R=mid-1; 103 } 104 int rr=L; 105 if (ll<i && rr>i) 106 { 107 int x1=lower_bound(sl+1,sl+1+tl,ll)-sl,x2=upper_bound(sl+1,sl+1+tl,i-1)-sl-1, 108 y1=lower_bound(sr+1,sr+1+tr,i+1)-sr,y2=upper_bound(sr+1,sr+1+tr,rr)-sr-1; 109 if (x1<=x2 && y1<=y2) 110 { 111 // cout<<i<<' '<<x1<<' '<<x2<<' '<<y1<<' '<<y2<<"!!\n"; 112 op[++lp]=(Ope){x1,y1,y2,1}; 113 op[++lp]=(Ope){x2+1,y1,y2,-1}; 114 } 115 } 116 } 117 118 tt.clear(tr); 119 sort(op+1,op+1+lp); 120 int tmp=0; 121 for (int i=1,j=1;i<=tl;i++) 122 { 123 while (j<=lp && op[j].x==i) tt.add(op[j].y1,op[j].y2,op[j].v),j++; 124 tmp=max(tmp,tt.a[1].Max); 125 } 126 127 ans-=tmp*2; 128 printf("%lld\n",ans); 129 return 0; 130 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号