BZOJ4385: [POI2015]Wilcze doły

$n \leq 2000000$的正数列，有一次机会把一段长度不超过$d$的数变成0，问最长的和不超过$p$的序列。

选的$d$区间一定是答案区间$[L,R]$的最大字段和。可以证明$R$往右时$L$不会往左。反证一下，假如出现了这种情况：

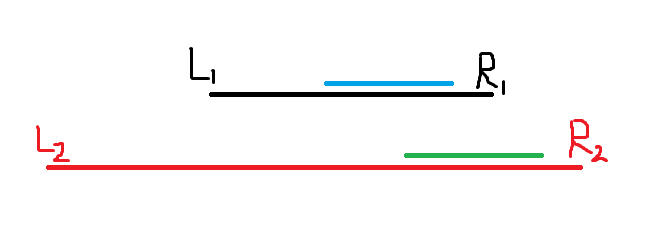
其中蓝色和绿色表示选中的$d$区间（绿不可能在R1左边，否则要么与蓝是最大子段和相悖，要么$L_1$还能再往左延伸到$L_2$）。然后，把这两段切一下：

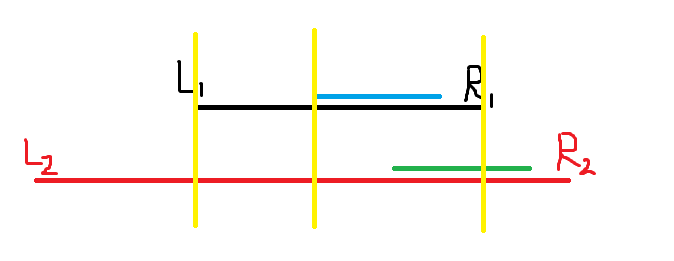
左边黄色那段两边一样多，右边黄色那段上面要比下面小（去掉蓝绿后），因为蓝色那段是这一小黄段的最大$d$子段和，绿色那段又不到$d$又不是最大，所以剩下那一部分肯定下面的大。既然如此，那$L_1$延伸到$L_2$处都是没有问题的，得证。

知道这个事情之后，就双指针扫下，至于最大子段和，可以搞一个值递减下标递增的单调队列。

//#include<iostream>
#include<cstring>
#include<cstdio>
//#include<math.h>
//#include<set>
//#include<queue>
//#include<bitset>
//#include<vector>
#include<algorithm>
#include<stdlib.h>
using namespace std;

#define LL long long
int qread()
{
    char c; int s=0,f=1; while ((c=getchar())<'0' || c>'9') (c=='-') && (f=-1);
    do s=s*10+c-'0'; while ((c=getchar())>='0' && c<='9'); return s*f;
}

//Pay attention to '-' , LL and double of qread!!!!

int n,D; LL m;
#define maxn 2000011
int a[maxn]; LL sum[maxn];
int que[maxn],head=1,tail=1;

int main()
{
    n=qread(); scanf("%lld",&m); D=qread();
    for (int i=1;i<=n;i++) a[i]=qread(),sum[i]=sum[i-1]+a[i];
    
    int L=1,R=D,ans=D; LL tot=sum[D]; que[tail++]=D;
    for (R++;R<=n;R++)
    {
        while (head<tail && sum[R]-sum[R-D]>sum[que[tail-1]]-sum[que[tail-1]-D]) tail--;
        que[tail++]=R;
        tot+=a[R];
        while (tot-(sum[que[head]]-sum[que[head]-D])>m)
        {
            tot-=a[L];
            while (que[head]<L+D) head++;
            L++;
        }
        ans=max(ans,R-L+1);
    }
    printf("%d\n",ans);
    return 0;
}