BZOJ1126: [POI2008]Uci

$n \leq 100,m \leq 100$，$n*m$的01矩形，问从左下角开始往上走，每次转弯只能向右，不能经过重复点，不能撞到1，到达点$(x,y)$的方案数，$mod \ \ k$。

感人肺腑的细节题写了一天。。

可以发现他在做一个绕圈运动，运动的过程中逐渐限制自己的活动范围，因此可以用活动范围和射入方向表示状态（这样也就确定了它的位置），$f[L][R][U][D][0123]$--沿左边向上、沿上边向右、沿右边向下、沿下边向左射入矩形$[L,R,U,D]$的方案。如图：

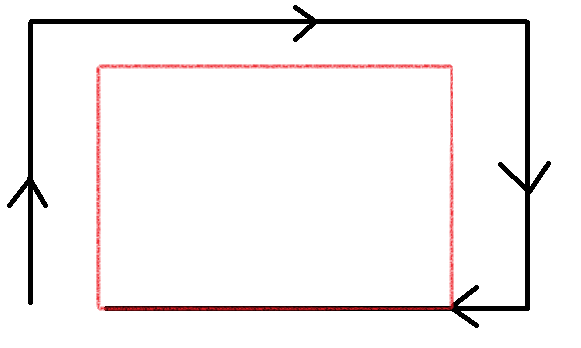
这样转移可以用一个前缀和转移。比如上转右的：

用纵方向一个前缀的蓝色矩形转移到右方向的一个矩形。这样就可以$O(1)$转移了。

由于四维开不下，要把L那一维滚动掉，所以记前缀和的时候，左转上那个数组不要清，那里实际保留了所有$L_2<L$转移到$L$的状态的前缀和。

记答案的时候，在目标处转弯时记录答案。注意最后一圈不要记重了。这句话是啥意思我也说不清，看代码吧QAQ

//#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
//#include<time.h>
//#include<complex>
#include<algorithm>
#include<stdlib.h>
using namespace std;

int n,m,mod,tx,ty;
#define maxn 111
int f[2][maxn][maxn][maxn][4],cur,sum[maxn][maxn][maxn][4],bl[maxn][maxn][4]; char s[maxn];
bool mp[maxn][maxn]; //0 up 1 right 2 down 3 left
int main()
{
    scanf("%d%d%d%d%d",&n,&m,&mod,&ty,&tx);
    for (int i=1;i<=n;i++)
    {
        scanf("%s",s+1);
        for (int j=1;j<=m;j++) mp[i][j]=(s[j]=='+');
    }
    
    for (int j=1;j<=m;j++)
    {
        bl[0][j][0]=0;
        for (int i=1;i<=n;i++) if (mp[i][j]) bl[i][j][0]=bl[i-1][j][0];
        else bl[i][j][0]=i;
    }
    for (int i=1;i<=n;i++)
    {
        bl[i][m+1][1]=m+1;
        for (int j=m;j;j--) if (mp[i][j]) bl[i][j][1]=bl[i][j+1][1];
        else bl[i][j][1]=j;
    }
    for (int j=1;j<=m;j++)
    {
        bl[n+1][j][2]=n+1;
        for (int i=n;i;i--) if (mp[i][j]) bl[i][j][2]=bl[i+1][j][2];
        else bl[i][j][2]=i;
    }
    for (int i=1;i<=n;i++)
    {
        bl[i][0][3]=0;
        for (int j=1;j<=m;j++) if (mp[i][j]) bl[i][j][3]=bl[i][j-1][3];
        else bl[i][j][3]=j;
    }
    cur=0; for (int i=1;i<=n;i++) sum[m][i][n][0]=1;
        
    int ans=0;
    for (int L=2;L<=ty+1;L++)
    {
        cur^=1;
        for (int R=m;R>=ty;R--) for (int U=1;U<=tx;U++) for (int D=max(U,tx);D<=n;D++)
        {
            sum[R][U][D][1]=sum[R+1][U][D][1];
            f[cur][R][U][D][1]=0;
            if (bl[D][L-1][0]<U)
            {
                f[cur][R][U][D][1]=sum[R][U][D][0];
                sum[R][U][D][1]+=f[cur][R][U][D][1]; sum[R][U][D][1]-=sum[R][U][D][1]>=mod?mod:0;
            }
            if (L-1==ty && U==tx) ans+=f[cur][R][U][D][1],ans-=ans>=mod?mod:0;
        }
        if (L==ty+1) break;
        for (int D=n;D>=tx;D--) for (int R=ty;R<=m;R++) for (int U=2;U<=tx+1;U++)
        {
            sum[R][U][D][2]=sum[R][U][D+1][2];
            f[cur][R][U][D][2]=0;
            if (bl[U-1][L-1][1]>R)
            {
                f[cur][R][U][D][2]=sum[R][U-1][D][1];
                sum[R][U][D][2]+=f[cur][R][U][D][2]; sum[R][U][D][2]-=sum[R][U][D][2]>=mod?mod:0;
            }
            if (U-1==tx && R==ty) ans+=f[cur][R][U][D][2],ans-=ans>=mod?mod:0;
        }
        for (int D=n;D>=tx;D--) for (int R=ty;R<=m;R++) sum[R][1][D][2]=sum[R][1][D+1][2];
        for (int U=1;U<=tx;U++) for (int D=max(tx,U);D<=n;D++) for (int R=ty-1;R<m;R++)
        {
            f[cur][R][U][D][3]=0;
            if (bl[U][R+1][2]>D)
            {
                f[cur][R][U][D][3]=sum[R+1][U][D][2];
                sum[R][U][D][3]+=f[cur][R][U][D][3]; sum[R][U][D][3]-=sum[R][U][D][3]>=mod?mod:0;
            }
            if (D==tx && R+1==ty) ans+=f[cur][R][U][D][3],ans-=ans>=mod?mod:0;
        }
        for (int U=1;U<=tx;U++) for (int D=tx-1;D<=n;D++) for (int R=ty;R<=m;R++)
        {
            if (U) sum[R][U][D][0]=sum[R][U-1][D][0];
            f[cur][R][U][D][0]=0;
            if (bl[D+1][R][3]<L)
            {
                f[cur][R][U][D][0]=sum[R][U][D+1][3];
                sum[R][U][D][0]+=f[cur][R][U][D][0]; sum[R][U][D][0]-=sum[R][U][D][0]>=mod?mod:0;
            }
            if (D+1==tx && L==ty) ans+=f[cur][R][U][D][0],ans-=ans>=mod?mod:0;
        }
        for (int U=1;U<=tx;U++) for (int R=ty;R<=m;R++) sum[R][U][n][0]=sum[R][U-1][n][0];
    }
    printf("%d\n",ans);
    return 0;
}